스택
스택의 특성
-
물건을 쌓아 올리듯 자료를 쌓아 올린 형태의 자료구조이다.
-
스택에 저장된 자료는 선형 구조를 갖는다.
-
선형 구조 : 자료 간의 관계가 1대 1의 관계를 갖는다.
-
비선형구조 : 자료 간의 관계가 1대 N의 관계를 갖는다. (예 : 트리)
-
스택에 자료를 삽입하거나 스택에 자료를 꺼낼 수 있다.
-
마지막에 삽입한 자료를 가장 먼저 꺼낸다. 후입선출(LIFO, Last-In-First-Out)이라고 부른다.
-
예를 들어, 스택에 1,2,3 순으로 자료를 삽입한 후 꺼내면 역순으로 3,2,1 순으로 꺼낼 수 있다.
스택을 프로그램에서 구현하기 위해서 필요한 자료구조와 연산
자료구조 : 자료를 선형으로 저장할 저장소
-
배열을 사용할 수 있다.
-
저장소 자체를 스택이라고 부르기도 한다.
-
스택에서 마지막 삽입된 원소의 위치를 top이라 부른다.
연산
-
삽입 : 저장소에 자료를 저장한다. 보통 push라고 부른다.
-
삭제 : 저장소에서 자료를 꺼낸다. 꺼낸 자료는 삽입한 자료의 역순으로 꺼낸다. 보통 pop이라고 부른다.
-
스택이 공백인지 아닌지를 확인하는 연산 : isEmpty
-
스택에 top에 있는 item(원소)을 반환하는 연산 : peek
스택의 삽입/삭제 과정
- 빈 스택에 원소 A, B, C를 차례로 삽입 후 한번 삭제하는 연산 과정
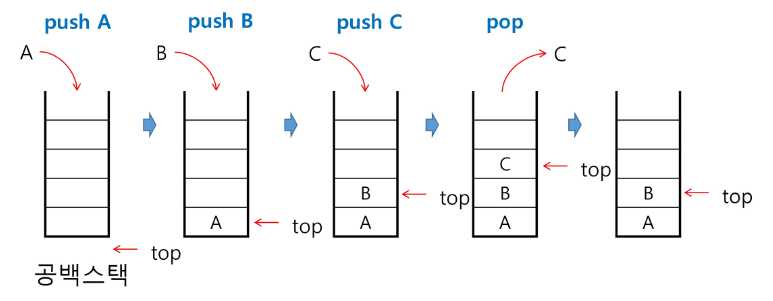
스택의 push 알고리즘
append 메소드를 통해 리스트의 마지막에 데이터를 삽입




def push(n, size):
global top
top += 1
if top == size:
print('overflow!')
else:
stack[top] = n
top = -1
size = 10
stack = [0] * size # 최대 10개 push
top += 1 # push 10
stack[top] = 10
top += 1 # push 20
stack[top] = 20
push(30, size)
while top >= 0:
top -= 1
print(stack[top+1])스택의 응용
스택 구현 고려 사항
1차원 배열을 사용하여 구현할 경우 구현이 용이하다는 장점이 있지만 스택의 크기를 변경하기가 어렵다는 단점이 있다.
이를 해결하기 위한 방법으로 저장소를 동적으로 할당하여 스택을 구현하는 방법이 있다. 동적 연결리스트를 이용하여 구현하는 방법을 의미한다. 구현이 복잡하다는 단점이 있지만 메모리를 효율적으로 사용한다는 장점을 가진다. 스택의 동적 구현은 생략한다.

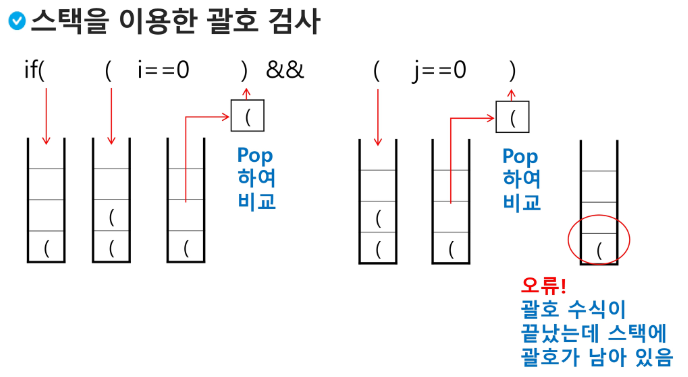
닫는 괄호인데 스택이 비어있으면 오류!
괄호를 조사하는 알고리즘 개요
-
문자열에 있는 괄호를 차례대로 조사하면서 왼쪽 괄호를 만나면 스택을 삽입하고, 오른쪽 괄호를 만나면 스택에서 top 괄호를 삭제한 후 오른쪽 괄호와 짝이 맞는지를 검사한다.
-
이때, 스택이 비어 있으면 조건 1 또는 조건 2에 위배되고 괄호의 짝이 맞지 않으면 조건 3에 위배된다.
-
마지막 괄호까지를 조사한 후에도 스택에 괄호가 남아있으면 조건 1에 위배된다.
스택의 응용
Function Call
프로그램에서 함수 호출과 복귀에 따른 수행 순서를 관리
- 가장 마지막에 호출된 함수가 가장 먼저 실행을 완료하고 복귀하는 후입선출 구조이므로, 후입선출 구조의 스택을 이용하여 수행 순서 관리
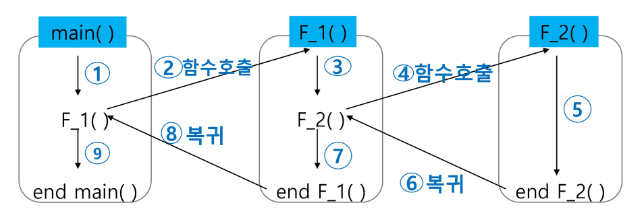
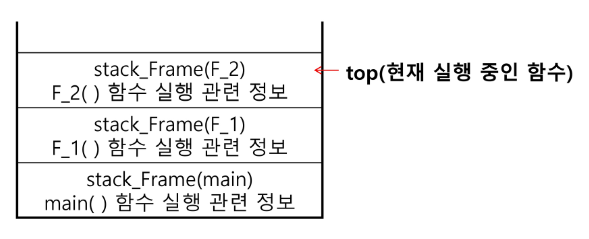
- 함수 호출이 발생하면 호출한 함수 수행에 필요한 지역 변수, 매개변수 및 수행 후 복귀할 주소 등의 정보를 스택 프레임(stack frame)에 저장하여 시스템 스택에 삽입
재귀호출
재귀 호출
필요한 함수가 자신과 같은 경우 자신을 다시 호출하는 구조
함수에서 실행해야 하는 작업의 특성에 따라 일반적인 호출 방식보다 재귀호출방식을 사용하여 함수를 만들면 프로그램의 크기를 줄이고 간단하게 작성
- 재귀 호출의 예) factorial

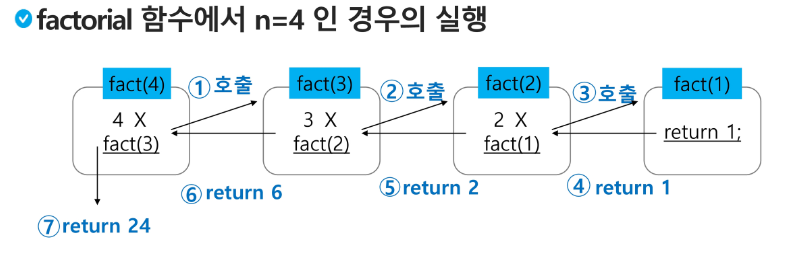
피보나치


def f(i, k) : # i 현재 위치, k 목표
if i == k:
return
else:
print(arr[i])
f(i+1, k)
arr = [10, 20, 30]
N = len(arr)
f(0, N)def f(i, k) : # i 현재 위치, k 목표
if i == k:
print(brr)
else:
brr[i] = arr[i]
f(i+1, k)
arr = [10, 20, 30]
N = len(arr)
brr = [0] * N
f(0, N)Memoization
피보나치 수를 구하는 함수를 재귀함수로 구현한 알고리즘은 엄청난 중복 호출이 존재한다는 문제점이 있다.
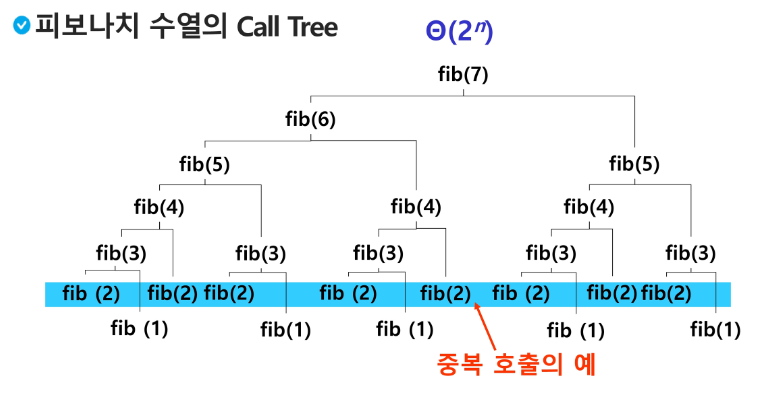
Memoization
메모이제이션(memoization)은 컴퓨터 프로그래밍을 실행할 때 이전에 계산한 값을 메모리에 저장해서 매번 다시 계산하지 않도록 하여 전체적인 실행속도를 빠르게 하는 기술이다. 동적 계획법의 핵심이 되는 기술이다.
'memoization'은 글자 그대로 해석하면 '메모리에 넣기(to put in memory)'라는 의미이며 '기억되어야 할 것' 이라는 뜻의 라틴어 memorandum에서 파생되었다. 흔히 '기억하기', '암기하기' 라는 뜻의 memorization과 혼동하지만, 정확한 단어는 memoization 이다. 동사형은 memoize이다.


def fibo(n):
global cnt
cnt += 1
if n < 2:
return n
else:
return fibo(n-1) + fibo(n-2)
def fibo_memo(n):
global cnt
cnt += 1
if n != 0 and memo[n] == 0:
memo[n] = fibo_memo(n-1) + fibo_memo(n-2)
return memo[n]
cnt = 0
n = 7
print(fibo(7), cnt)
cnt = 0
memo = [0] * (n+1)
memo[0] = 0
memo[1] = 1
print(fibo_memo(n), cnt)
print(memo)
