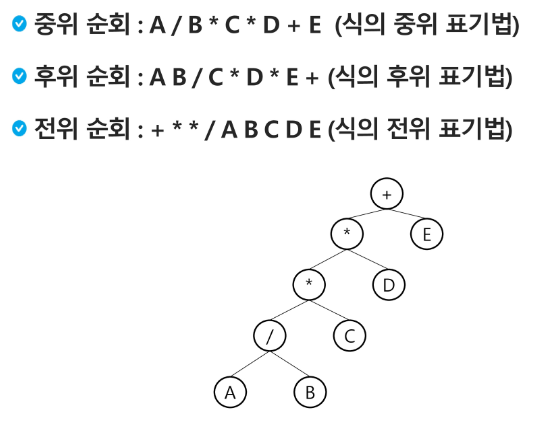
수식 트리
수식 트리
수식을 표현하는 이진 트리
수식 이진 트리 (Expression Binary Tree) 라고 부르기도 함.
연산자는 루트 노드이거나 가지 노드
피연산자는 모두 잎 노드
이진 탐색 트리
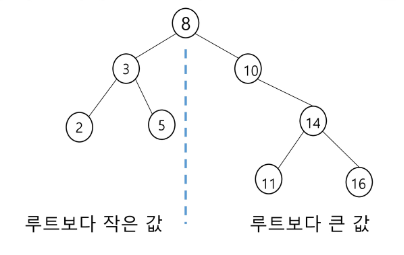
이진 탐색 트리
탐색 작업을 효율적으로 하기 위한 자료 구조
모든 원소는 서로 다른 유일한 키를 갖는다.
key(왼쪽 서브 트리) < key(루트 노드) < key (오른쪽 서브트리)
왼쪽 서브트리와 오른쪽 서브트리도 이진 탐색 트리다.
중위 순회 하면 오름차순으로 정렬된 값을 얻을 수 있다.
탐색 연산
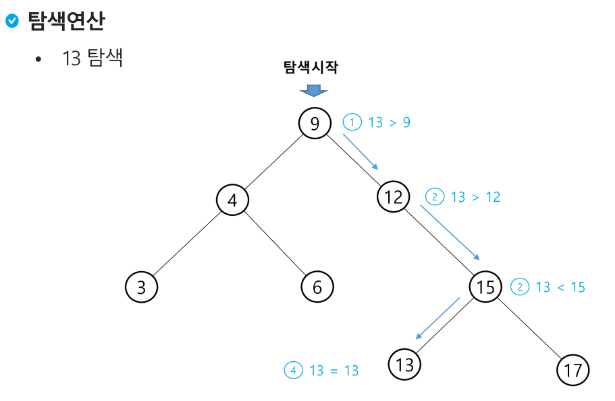
루트에서 시작한다.
탐색할 키 값 x를 루트 노드의 키 값과 비교한다.
-
(키 값x = 루트 노드의 키 값)인 경우 : 원하는 원소를 찾았으므로 탐색 연산 성공
-
(키 값x < 루트 노드의 키 값)인 경우 : 루트 노드의 왼쪽 서브트리에 대해서 탐색연산 수행
-
(키 값x > 루트 노드의 키 값)인 경우 : 루트 노드의 오른쪽 서브트리에 대해서 탐색 연산 수행
서브트리에 대해서 순환적으로 탐색 연산을 반복한다.
삽입 연산
- 먼저 탐색 연산을 수행
-
삽입할 원소와 같은 원소가 트리에 있으면 삽입할 수 없으므로, 같은 원소가 트리에 있는지 탐색하여 확인한다.
-
탐색에서 탐색 실패가 결정되는 위치가 삽입 위치가 된다.
- 탐색 실패한 위치에 원소를 삽입한다.
- 다음 예는 5을 삽입하는 예이다.
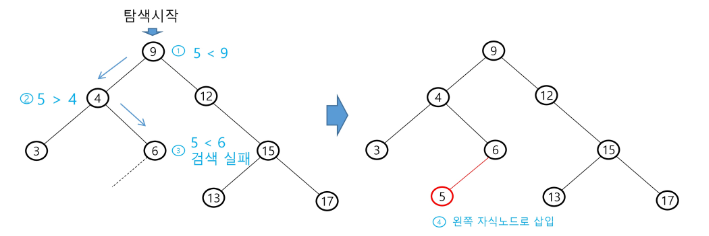
이진 탐색 트리의 성능
탐색(searching), 삽입(insertion), 삭제(deletion) 시간은 트리의 높이 만큼 시간이 걸린다.
- O(h), h : BST 의 깊이 (height)
평균의 경우
-
이진 트리가 균형적으로 생성되어 있는 경우
-
O(log n)
최악의 경우
-
한쪽으로 치우친 경사 이진트리의 경우
-
O(n)
-
순차 탐색과 시간복잡도가 같다.
검색 알고리즘의 비교
배열에서의 순차 검색 : O(N)
정렬된 배열에서의 순차 검색 : O(N)
정렬된 배열에서의 이진 탐색 : O(log N)
- 고정 배열 크기와 삽입, 삭제 시 추가 연산 필요
이진 탐색 트리에서의 평균 : O(log N)
-
최악의 경우 : O(N)
-
완전 이진트리 또는 균형 트리로 바꿀 수 있다면 최악의 경우를 없앨 수 있다.
-
새로운 원소를 삽입할 때 삽입 시간을 줄인다.
-
평균과 최악의 시간이 같다. O(log N)
해쉬 검색 : O(1)
- 추가 저장공간 필요
삭제 연산
삭제 연산에 대해 알고리즘을 생각해봅시다.
다음 트리에 대하여 13, 12, 9를 차례로 삭제해 보자.
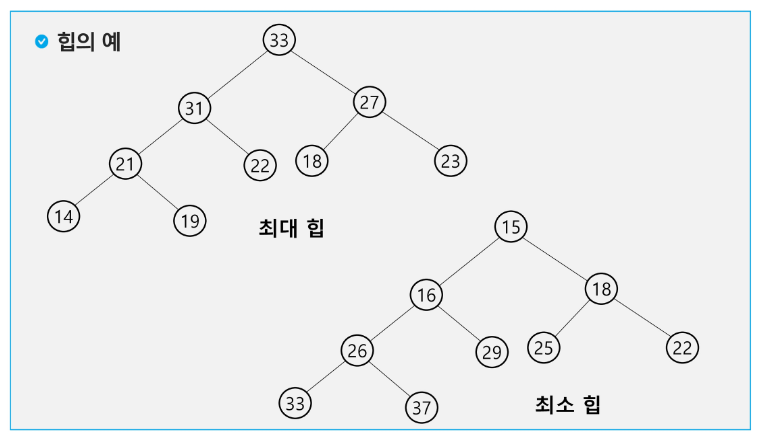
힙
힙
완전 이진 트리에 있는 노드 중에서 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾기 위해서 만든 자료구조
최대 힙(max heap)
키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리
{부모노드의 키 값 > 자식 노드의 키 값}
루트 노드 : 키 값이 가장 큰 노드
최소 힙 (min heap)
키 값이 가장 작은 노드를 찾기 위한 완전 이진 트리
{부모노드의 키 값 < 자식 노드의 키 값}
루트 노드 : 키 값이 가장 작은 노드
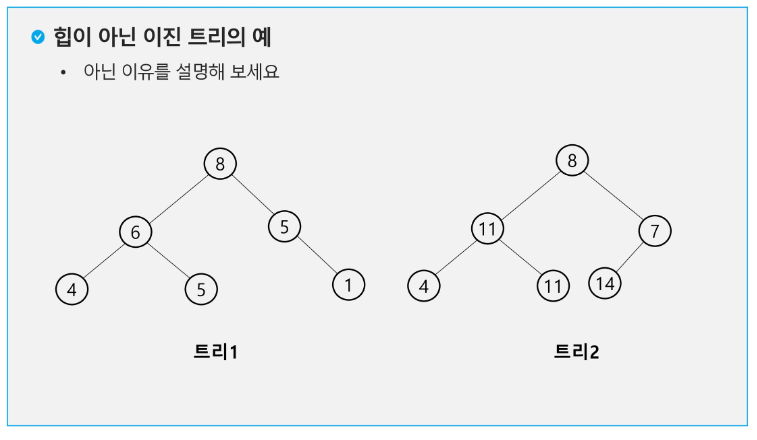
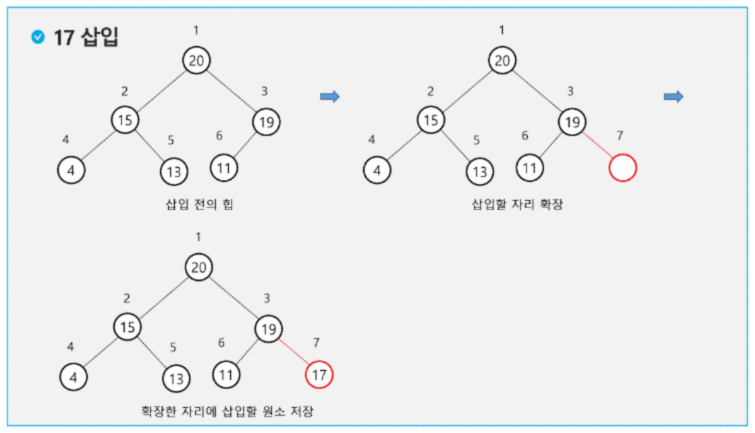
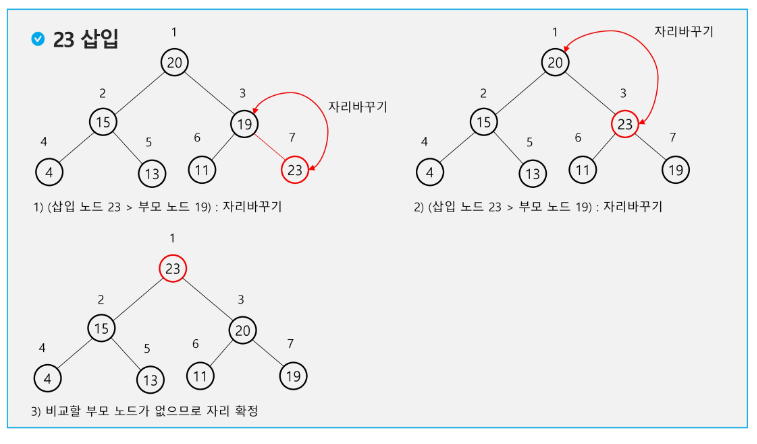
'''
2 5 3 6 4
마지막 노드를 추가하고
'''
# 최대 힙
def enq(n):
global last
last += 1 # 마지막 노드를 추가 (완전 이진 트리 유지)
h[last] = n # 마지막 노드에 데이터 삽입
c = last # 부모 > 자식 비교를 위해
p = c // 2 # 부모 번호 계산
while p >= 1 and h[p] < h[c]: # 부모가 존재하고 더 작으면
h[p], h[c] = h[c], h[p] # 부모, 자식 교환
c = p
p = c // 2
N = 10 # 필요한 노드 수
h = [0]*(N+1) # 최대 힙
last = 0 # 힙의 마지막 노드 번호
enq(2)
enq(5)
enq(3)
enq(6)
enq(4)
힙연산 - 삭제
힙에서는 루트 노드의 원소만을 삭제할 수 있다.
루트 노드의 원소를 삭제하여 반환한다.
힙의 종류에 따라 최대값 또는 최소값을 구할 수 있다.
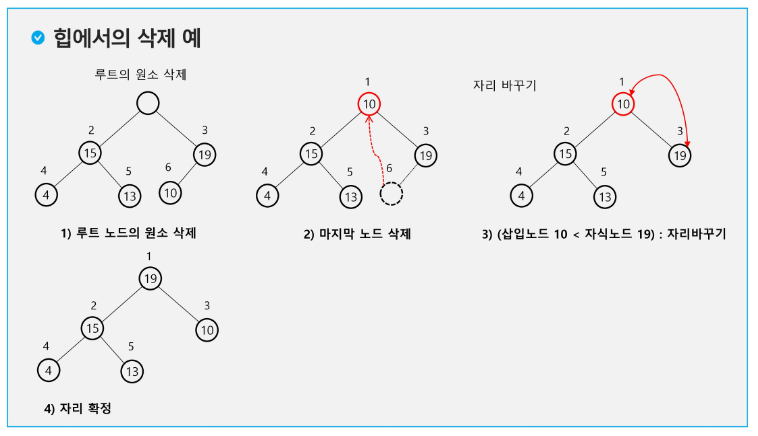
def deq():
global last
tmp = h[1] # 루트의 키 값 보관
h[1] = h[last]
last -= 1 # 마지막 노드를 삭제 - 접근할 인덱스 줄여놓으면 다음번엔 알아서 거기다 입력되니까
p = 1 # 새로 옮긴 루트 insert와 다르게 p 값으로 먼저 접근
c = p * 2
while c <= last : # 자식이 있으면
if c + 1 <= last and h[c] < h[c+1]: # 오른쪽 자식이 있고 힙의 왼쪽 자식과 오른쪽 자식을 비교해서 오른쪽 자식이 더 크면
c += 1
if h[p] < h[c]: # 자식이 더 크면
h[p], h[c] = h[c], h[p]
p = c
c = p * 2
else: # 부모가 더 크면
break # 비교 중단
return tmp # 보관했던 tmp return
N = 10 # 필요한 노드 수
h = [0]*(N+1) # 최대 힙
last = 0 # 힙의 마지막 노드 번호
enq(2)
enq(5)
enq(3)
enq(6)
enq(4)
while(last > 0):
print(deq())완전 이진 트리 -> 마지막 노드만 삭제 가능
