
📖 시간 복잡도
주어진 문제를 해결하기 위한 연산 횟수로 시간제한 1초라면 약 1억번의 연산 안에 답이 나오도록 해야 한다.
✫ 시간 복잡도 유형
빅-오메가 : 최선일 때(best case)의 연산 횟수를 나타낸 표기법. 한 번에 답이 나오는 경우
빅-세타 : 보통일 때(average case)의 연산 횟수를 나타낸 표기법. n/2 안에 답이 나오는 경우
빅-오 : 최악일 때(worst case)의 연산 횟수를 나타낸 표기법.
실제로 코테에서는 최악을 염두해야 하므로 빅-오 표기법을 기준으로 수행 시간을 계산해야 한다. 다양한 테스트 케이스를 수행해 모든 케이스를 통과해야 하기 때문에.
✫ 수행 속도
O(N!) -> O(2ⁿ) -> O(N²) -> O(NlongN) -> O(N) -> O(logN) -> O(1)
✫ 데이터
시간 제한과 입력에서 데이터 개수를 잘 봐야한다.
시간 복잡도는 항상 최악일 때로 데이터의 크기가 가장 클 때를 기준으로 한다.
연산 횟수 계산 방법 : 알고리즘 시간 복잡도 X 데이터의 크기
ex) 버블 정렬은 시간 복잡도가 n². 데이터 크기가 100만, 제한 시간이 2초라면 100만의 제곱을 했을 때 제한 시간(2억)보다 크게 되어 부적합한 알고리즘이 된다. 병합 정렬의 경우라면 nlogn으로 제한 시간(2억)보다 작아서 적합한 알고리즘이 된다.
✫ 나의 코드 시간 복잡도
내 코드가 현재 시간 복잡도에 맞게 짜져있는지 확인을 해야 한다.
시간 복잡도 도출 기준
1. 상수는 시간 복잡도 계산에서 제외한다.
2. 가장 많이 중첩된 반복문의 수행 횟수가 시간 복잡도의 기준이 된다.
연산 횟수가 O(N)
import java.util.*;
class Solution {
public static void main(String args[]){
int N = 100000;
int cnt = 0;
for(int i=0; i<N; i++){
System.out.println("연산 횟수: " + cnt++);
}
}
}위 코드에서 for문이 3개 있다면 연산 횟수는 3N이 된다.
하지만 상수는 무시하므로 O(N)이 된다.
이중 for문이면 시간 복잡도는 N².
이중 for문 이외에 다른 일반 for문이 여러 개 있어도 도출 원리의 기준에 따라 변화없이 N²으로 유지된다.
즉 가장 많은 중첩문을 봐야 한다.
결과가 시간초과가 발생하는 경우 내 로직이 효율적으로 짜져있는지를 확인해야 한다.
📖 디버깅
코테하면서 디버깅을 하면 좋지만 기업 코테에서는 IDE 사용 못하므로 참고만.
자주 실수하는 오류 4가지
1. 변수 초기화 오류
-
arrayindexoutofboundsexception (인덱스 오류로 항상 나오면 멘붕오는 오류.)
나의 해결 방법 -> 어느 줄에서 오류가 나타난 건지 찾기가 어려우므로 나올 만한 곳을 지워보고 코드를 실행해본다. 오류가 그대로라면 다시 복구하고 오류가 사라졌다면 정확히 어느 줄인지 파악하기 위해 다시 조금씩 지워보면서 확인. -
변수 사용 오류
-
자료형 범위 오류 -> 처음부터 int형으로 하는 것이 아닌 long으로 하는 것이 좋지만 습관이 되어 있지 않으므로 일단 long으로 시작을 하지 않았다면 long으로 바꿔보기.
📖 구간 합
공식 : S[j] - S[i-1]
ex) 배열 A = [15, 13, 10, 7, 3, 12] 일 때 인덱스 2 ~ 5까지의 합을 구하고 싶다면 S[5] - S[1]의 값을 구하면 된다.
(S[5]는 A[0] ~ A[5]까지의 합)
A[2] ~ A[5] 구간 합 과정
S[5] = A[0] + A[1] + A[2] + A[3] + A[4] + A[5]
S[1] = A[0] + A[1]
S[5] - S[1] = A[2] + A[3] + A[4] + A[5]
📖 우선순위 큐
값이 들어간 순서와 상관없이 우선순위가 높은 데이터가 먼저 나오는 자료구조.
최대힙, 최소힙으로 트리구조로 되어있음.
➺ Stack은 먼저 들어간 데이터가 가장 늦게 나오는 LIFO(Last In First Out) 방식이고 Queue는 먼저 들어간 데이터가 먼저 나오는 FIFO(First In First Out) 방식입니다.
📖 버블 정렬
데이터의 인접 요소끼리 비교하고, swap 연산을 수행하며 정렬하는 방식.
시간 복잡도 : O(n^2)
다른 정렬 알고리즘보다 속도가 느림.
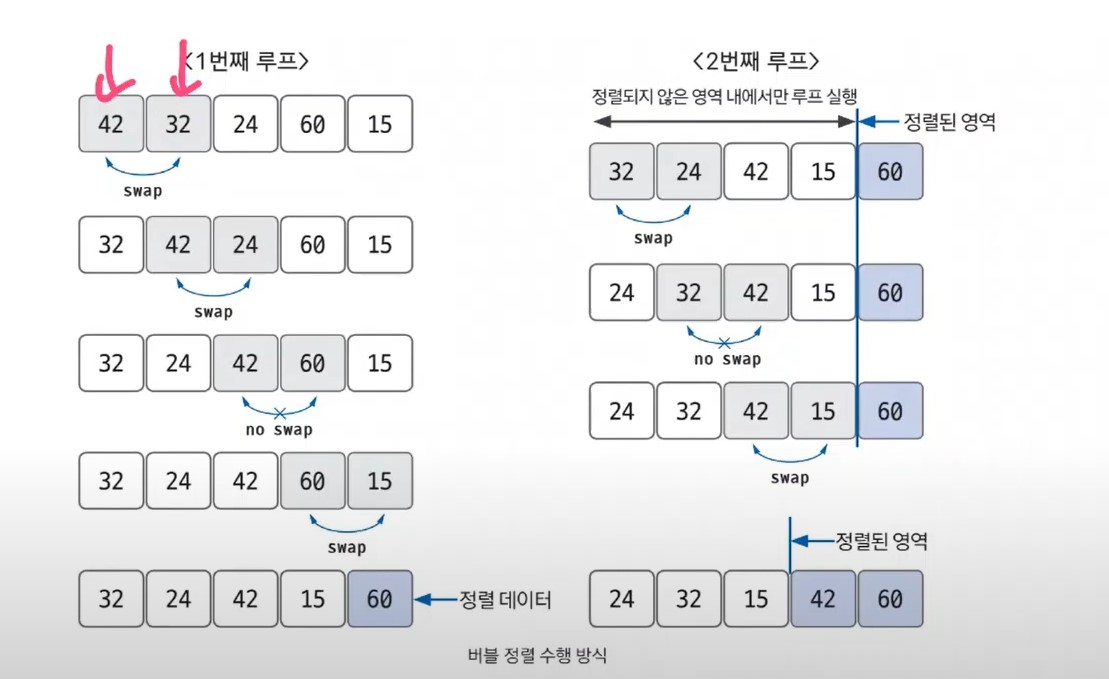
오름차순으로 정렬.
만약 어느 한 루프에서 swap이 한 번도 발생하지 않았다면 프로세스 종료
📖 선택 정렬
최소값이나 최대값을 찾고, 정렬하지 않고 남은 정렬 부분의 가장 앞에 있는 데이터와 swap하는 정렬.
시간 복잡도 : O(n^2)
버블 정렬과 시간복잡도가 같음.
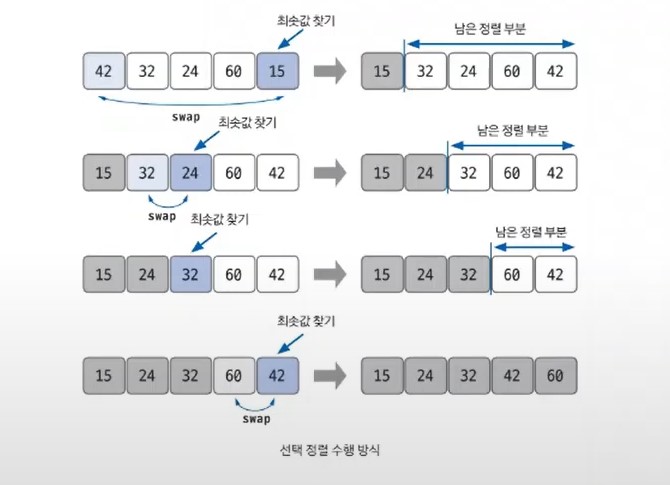
📖 삽입 정렬
이미 정렬된 데이터 범위에 정렬되지 않은 데이터를 적절한 위치에 삽입시켜 정렬하는 방식.
시간 복잡도 : O(n^2)
버블, 선택 정렬과 같음.
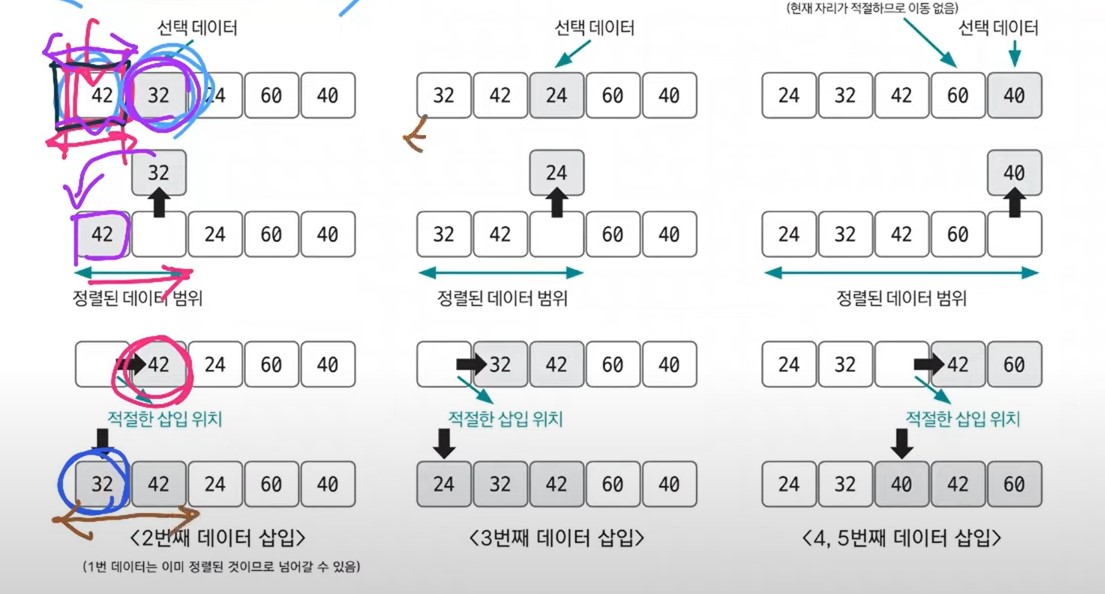
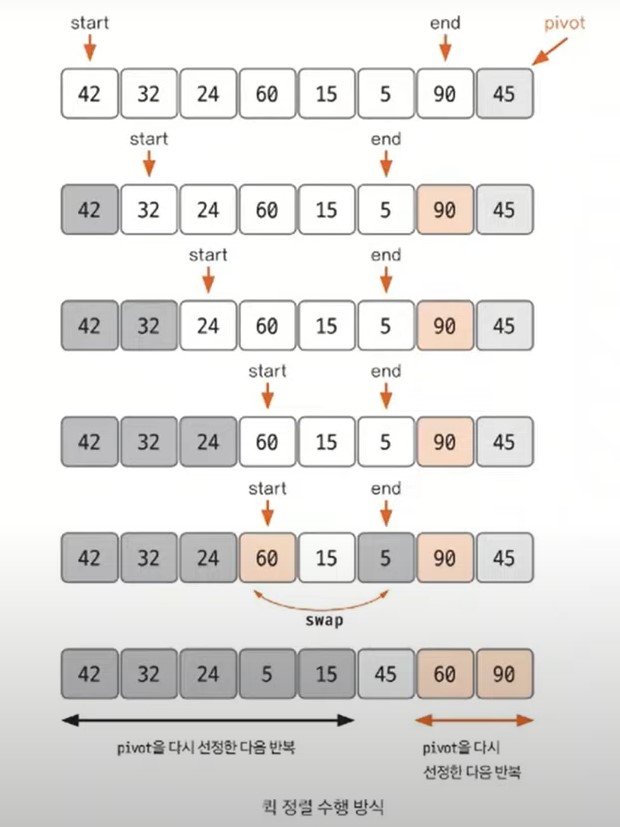
📖 퀵 정렬
기준 값(pivot)을 선정해서 해당 값보다 작은 데이터와 큰 데이터로 분류하는 것을 반복해 정렬.
시간 복잡도 : O(nlogn)
최악의 경우 O(n^2)
📖 병합 정렬
분할 정복 방식을 사용해 데이터를 분할하고 분할한 집합을 정렬하며 합치는 정렬.
시간 복잡도 : O(nlogn)
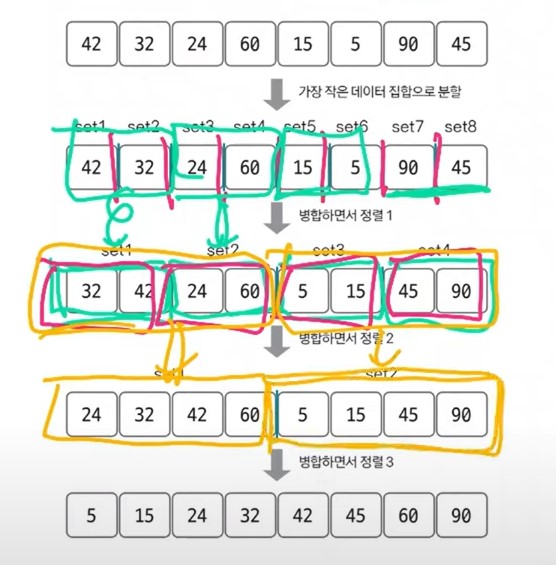
2개의 그룹을 병합하는 과정.
투 포인터 개념을 사용하여 왼쪽, 오른쪽 그룹을 병합.
왼족 포인터와 오른쪽 포인터의 값을 비교하여 작은 값을 결과 배열에 추가하고 포인터를 오른쪽으로 1칸 이동.
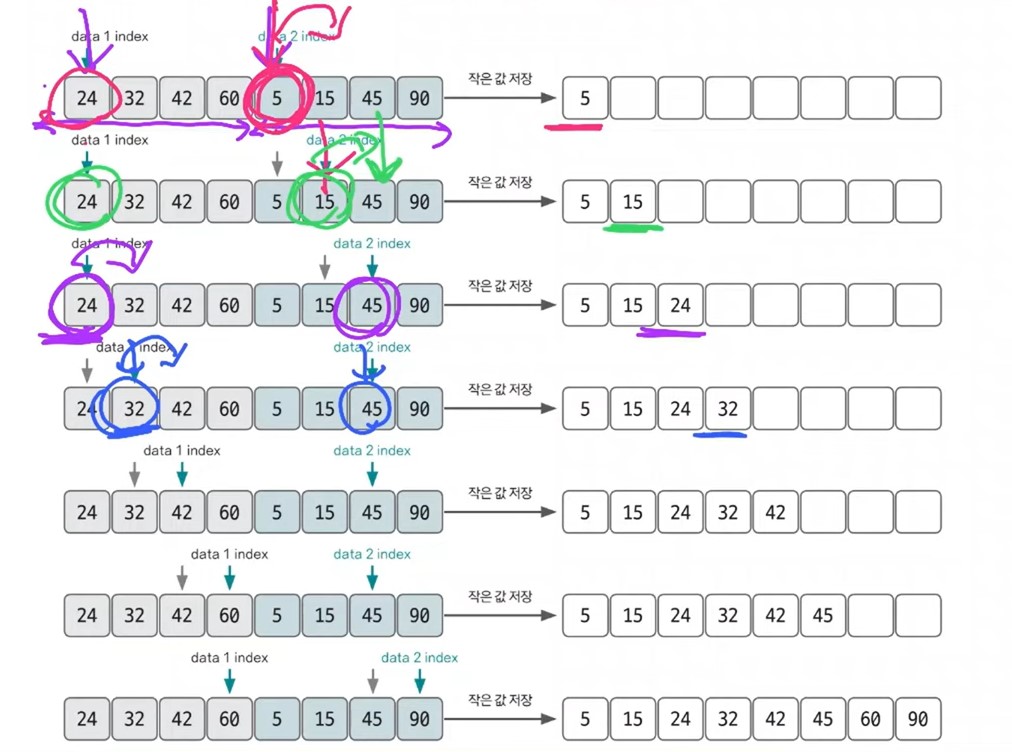
2개의 데이터를 묶어서 가는데 총 N번의 데이터가 필요하고 이 N번의 데이터를 병합하는데 필요한 작업이 logN이므로 시간 복잡도가 O(nlogn)
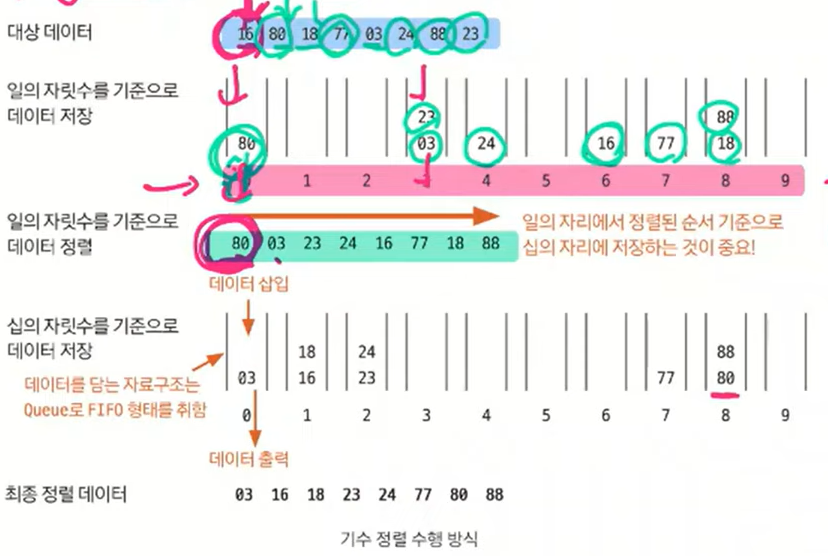
📖 기수 정렬 (시간 복잡도 가장 짧음.)
값을 비교하지 않고 값은 놓고 비교할 자릿수를 정한 다음 해당 자릿수만 비교하는 정렬.
시간 복잡도 : O(kn)
0~9까지의 숫자를 담기 위해서 10개의 큐를 사용한다. 그리고 각 큐는 값의 자릿수를 대표한다.
처음에 일의 자릿수를 기준으로 데이터를 저장한다.
큐가 0~9까지 있다면 일의 자릿수를 기준으로 배치해준다.
ex) 16이라면 일의 자릿수가 6이므로 6인 큐에 16을 저장.
그러면 일의 자릿수만 봤을 때 정렬이 된다.
십의 자릿수도 똑같이 큐에 배치. (백의 자리, 천의 자리도 똑같음.)
수의 자릿수마다 한 칸씩 올려가면서 N개를 탐색하므로 kn인 것이다.
📖 DFS
그래프 시작 노드에서 출발하여 탐색할 한 쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘.
📖 BFS
시작 노드에서 출발해 시작 노드를 기준으로 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘.
그리디
현재 상태에서 보는 선택지 중 최선의 선택지가 전체 선택지 중 최선의 선택지라고 가정하는 알고리즘.
