문제

나의 요약

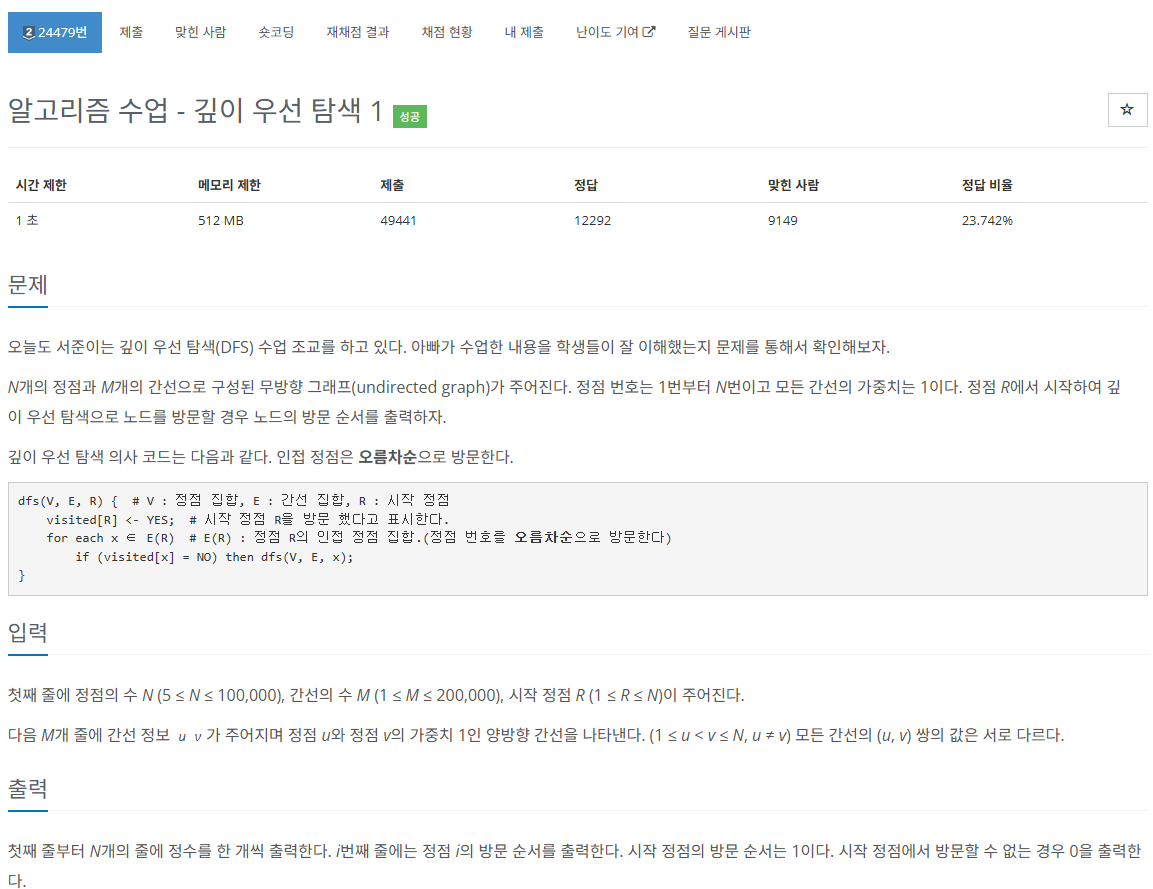
N 정점, M 간선 무방향 그래프. 정점 번호는 1~N. 가중치는 모두 1이다.
정점 R에서 시작해 DFS할경우 방문 순서 출력한다.

접근 방식

문제 이름부터 깊이 우선 탐색(DFS)라고 박혀 있어서 크게 접근을 고민할 일이 없었다. 대신 원래 DFS를 재귀 방식으로 푸는 것을 즐겨했는데, 아무래도 숫자가 커지면 최대 Call Stack 문제로 재귀로 푸는 것이 제한되니 Stack 자료구조를 이용한 방식으로 풀기로 했다.

풀이

#include <bits/stdc++.h>

using namespace std;

int N, M, R;
vector<vector<int> > graph;
vector<int> visitedOrder;

bool Compare(int i, int j)
{
	return j < i;
}

void Input()
{
	cin >> N >> M >> R;
	R--;
	
	visitedOrder.assign(N, 0);
	
	for(int n = 0; n < N; n++)
	{
		vector<int> v;
		graph.push_back(v);
	}
	
	for(int i = 0; i < M; i++)
	{
		int u, v;
		cin >> u >> v;
		u--; v--;
		
		graph[u].push_back(v); graph[v].push_back(u);
	}
	
	for(int n = 0; n < N; n++)
	{
		sort(graph[n].begin(), graph[n].end(), Compare);
	}
}

void DFS(int start)
{
	vector<bool> visited;
	visited.assign(N, false);
	
	stack<int> st;
	st.push(start);
	
	int visitedOrderNum = 0;
	while(!st.empty())
	{
		int now = st.top();
		st.pop();
		
		if(visited[now]) { continue; }
		
		visitedOrder[now] = ++visitedOrderNum;
		visited[now] = true;
		
		for(int i = 0; i < graph[now].size(); i++)
		{
			int next = graph[now][i];
			if(!visited[next])
			{
				st.push(next);
			}
		}
	}
}

void Output()
{
	for(int n = 0; n < N; n++)
	{
		cout << visitedOrder[n] << '\n';
	}
}

int main()
{
  	ios::sync_with_stdio(false);
  	cin.tie(NULL);
  	cout.tie(NULL);
  	
  	Input();
  	DFS(R);
  	Output();
}

DFS 함수에 집중해보자. stack<int> 형인 st에 처음 방문할 노드를 담아놓는다.
이후 st가 빌 때까지 다음의 과정을 반복한다.
1. st의 가장 위에 있는 요소를 꺼낸다.
2. 이것이 방문한 노드인지 확인한다.
2-1. 방문한 노드라면 다음 반복으로 넘어간다. (visited[now] == true)
2-2. 방문하지 않은 노드라면 단계를 이어간다.
3. 방문한 순서를 늘리고, 현재 노드의 방문 순서에 저장한다. (visitedOrder[now] = ++visitedOrderNum;)
4. 인접 노드들을 순회하며 st에 인접 노드들을 넣는다. 굳이 방문한 노드를 다시 넣을 필요는 없으니, 제외한다.

방문한 순서대로 1씩 늘려주며 저장을 하고, 이후에 출력만 하면 되는 문제이므로 다음의 과정만 진행하면 끝이 난다.

헤맨 지점

왜인지 자꾸 테스트케이스 출력과 다른 값이 출력되었다. 문제 설명에서 위의 하이라이트친 부분을 제대로 숙지하지 않았기 때문이었다..

인접 정점들을 오름차순으로 순회하면 되는 조건이었으므로, 각 정점에 대한 인접 정점을 graph[정점]에 내림차순으로 저장하였다. 내림차순인 이유는 생각해보면 간단한데, stack 자료구조의 특성상 맨 마지막에 추가한 노드부터 방문을 하기 때문이다. 따라서 내림차순으로 push하면 제일 값이 낮은 노드가 top이 되기 때문이다.

문제를 읽을 때 한번에 숙지하자.