문제

나의 요약

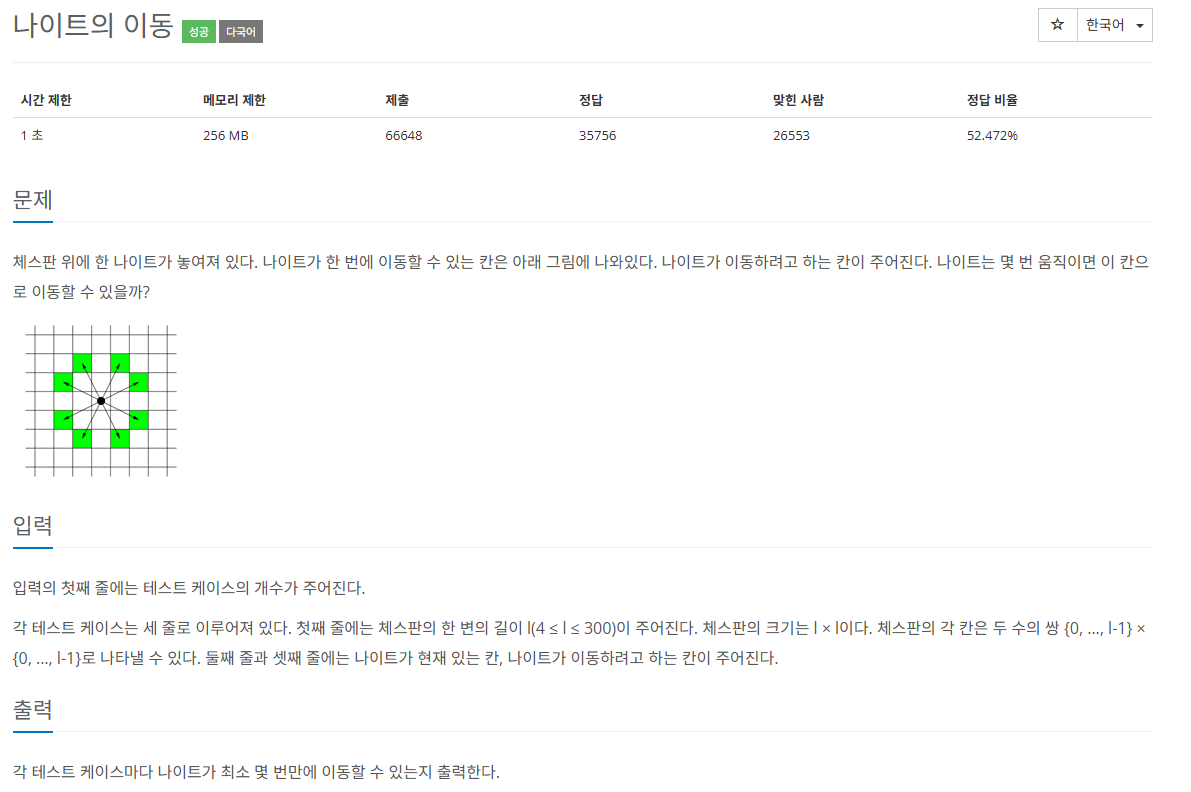
lxl 체스판에서 나이트의 초기 칸과, 이동하려는 칸이 주어진다. 나이트는 몇번 움직여야 해당 칸으로 이동할 수 있는가?

접근 방식

일단 탐색을 진행하면 되겠다고 생각했다. 한 변의 길이 l이 최대 300이므로 체스판은 아무리 커봐야 90000의 칸을 가진다. BFS, DFS 모두 가능할 것이라고 생각했지만, 이동을 하나하나 늘려가는 BFS가 문제와 더 구현이 깔끔하게 맞는다고 생각했다. 따라서 BFS로 바로 진행했다.

풀이

#include <bits/stdc++.h>
using namespace std;

int dx[] = {1, 2, 1, 2, -1, -2, -1, -2};
int dy[] = {2, 1, -2, -1, -2, -1, 2, 1};
int l;
pair<int, int> currentKnight;
pair<int, int> target;

bool CanGo(int x, int y)
{
	return (x >= 0 && x < l && y >= 0 && y < l);
}

void Solve()
{
	vector<vector<bool> > visited;
	for(int i = 0; i < l; i++)
	{
		vector<bool> v;
		v.assign(l, false);
		visited.push_back(v);
	}
	
	queue<pair<pair<int, int>, int> > q;
	q.push({{currentKnight.first, currentKnight.second}, 0});
	
	while(!q.empty())
	{
		int x = q.front().first.first;
		int y = q.front().first.second;
		int count = q.front().second;
		q.pop();
		
		if(visited[x][y]) { continue; }
		visited[x][y] = true;
		
		if(x == target.first && y == target.second)
		{
			cout << count << '\n';
			break;
		}
		
		for(int i = 0; i < 8; i++)
		{
			int nx = x + dx[i];
			int ny = y + dy[i];
			if(CanGo(nx, ny) && !visited[nx][ny])
			{
				q.push({{nx, ny}, count + 1});
			}
		}
	}
}

void Input()
{
	int T;
	cin >> T;
	
	for(int i = 0; i < T; i++)
	{
		cin >> l;
		int x, y;
		cin >> x >> y;
		currentKnight = {x, y};
		cin >> x >> y;
		target = {x, y};
		
		Solve();
	}
}

int main()
{
  	ios::sync_with_stdio(false);
  	cin.tie(NULL);
  	cout.tie(NULL);
  	
  	Input();
}

Solve 함수를 보면 큐 자료구조를 통해 BFS를 진행하는 것을 볼 수 있다. 큐 안에 pair형이 두 번이나 들어가 약간 어지러울 수 있으나, 각각 { {x좌표, y좌표}, 이동한 숫자}을 나타낸다는 걸 기억하면 어렵지 않다.

나머지는 CanGo 함수를 통해 다음 이동이 체스판을 벗어나는지 확인하는 것 이외엔 특별한 풀이는 없다.

회고

분명 어제 '한 단계 더 높여야겠다..' 라고 생각해놓고 즉시 까먹고 원래 단계의 문제를 풀어버렸다. 하필이면 내가 제일 자신 있는 BFS/DFS 문제라 15분 밖에 걸리지 않았다. 이건 그냥 내가 자신있는 부분에 걸렸을 뿐이니.. 앞으로는 정말 단계를 높여 부족한 부분을 채워보자.