11. Container With Most Water

문제 링크: https://leetcode.com/problems/container-with-most-water/

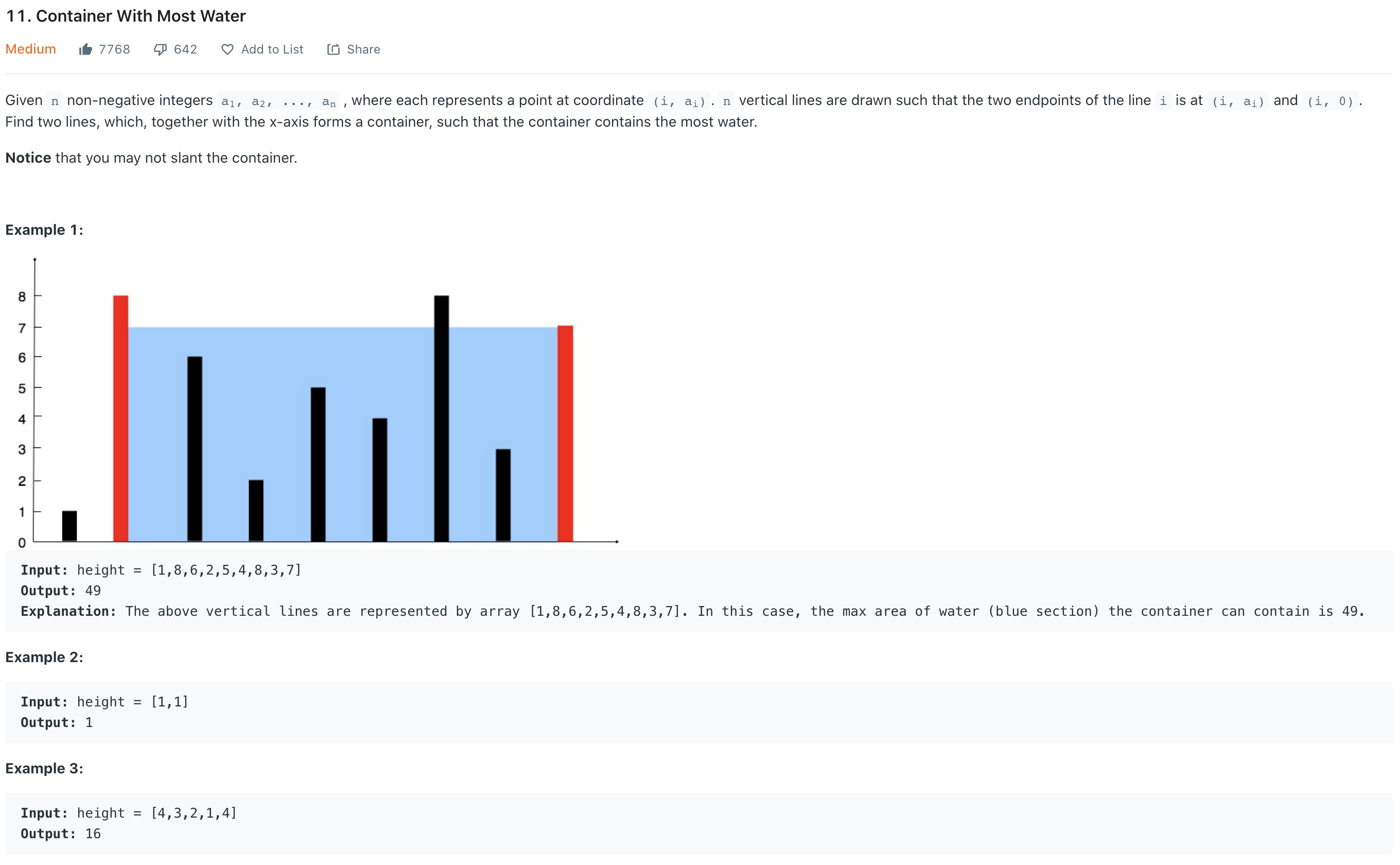
문제에 직관적인 그림이 있어서 이해하기 쉬웠다. 음수가 아닌 정수 배열이 주어지면, 그 배열의 원소 값을 가지는 수직선을 만들어 가장 많이 채울 수 있는 물의 양을 반환하는 문제이다.

Solution

1. Brute force

우선 Brute-force로 풀어 보자면, 선택할 수 있는 모든 두 쌍의 수직선을 높이로 한 후, 더 짧은 수직선만큼 물을 채워 그 양의 최댓값을 구하면 될 것 같다. 사이에 있는 수직선의 높이가 어떻든 양 끝의 두 수직선 중 짧은 수직선에 의해 채울 수 있는 물의 높이가 결정된다는 점이 재미있었다.

class Solution {
    public int maxArea(int[] height) {
        int containerHeight=0;
        int containerWidth=0;
        int water=0;
        
        int mostWater = 0;
        for(int i=0; i<height.length-1; i++) {
            for(int j=i+1; j<height.length; j++) {
                containerHeight = Math.min(height[i], height[j]); 
                containerWidth = j-i;
                water = containerHeight*containerWidth;
                mostWater = (water>mostWater) ? water: mostWater;
            }
        }
        
        return mostWater;
    }
}

mostWater는 Integer.MIN_VALUE로 초기화 해야 하는 것이 아닌가 하겠지만, 물의 양은 0 미만이 될 수 없고, 수직선의 높이가 모두 0일 때도 맞는 답을 반환하기 위해 0으로 초기화 했다.

코드를 좀 더 가독성 있게 다듬어 보면,

class Solution {
    public int maxArea(int[] height) {
        int mostWater = 0;
        for(int i=0; i<height.length-1; i++) {
            for(int j=i+1; j<height.length; j++) {
                mostWater = Math.max(mostWater,(j-i)*Math.min(height[i], height[j])); 
            }
        }
        
        return mostWater;
    }
}

mostWater 변수 하나만 선언하고 코드를 작성할 수 있다.
(단점은 Math함수를 두 번이나 사용해 위의 방법보다 실행 시간이 좀 더 오래 걸린다.)

Brute force로 풀어서 Time Limit Exeeded가 날 줄 알았더니 Accept가 떴다! 과연 O(N^2)라 실행 시간은 오래 걸린다.

2. DP with 2-pointer approach

이 문제를 보자마자 원소의 높이에 따른 물의 양 최대값을 찾는 문제이니 DP가 떠올랐다.
dp[i]=채울 수 있는 물의 양 (i=높이)로 최대값을 찾으면 될 것 같다.

특이점은 i가 가장 클 때 dp[i]가 최대값을 갖진 않는다는 점, i에 따라 높이 i 이상인 가장 먼 수직선 두 개를 찾아야 한다는 점이다. 배열을 한 번 순회할 땐 O(N)의 비용밖에 들지 않으니, 이 방법을 진행해보기로 했다.

이에 dp배열의 인덱스인 높이 i를 파라미터로 가지며, 높이 i로 만들 수 있는 최대 넓이를 반환해주는 메소드 findMaxArea()를 만들었다.

class Solution {
    public int findMaxArea(int[] height, int length) {
        int start=0; 
        int end=0;
        
        for(int i=0; i<height.length; i++) {
            if(height[i]>=length) {
                start=i;
                break;
            }
        }
        
        for(int i=height.length-1; i>=0;i--) {
            if(height[i]>=length) {
                end=i;
                break;
            }
        }
        return (end-start)*length;
    }
    
    public int maxArea(int[] height) {
        int[] tempHeight = new int[height.length];
        int mostWater = 0;
        int maxHeight=0;
        
        for(int i=0; i<height.length; i++) {
            tempHeight[i] = height[i];
        }
        Arrays.sort(tempHeight);
        
        maxHeight=tempHeight[tempHeight.length-2];
        
        int[] dp = new int[maxHeight+1]; // dp[i] = most water
        for(int i=0; i<=maxHeight; i++) {
            dp[i] = findMaxArea(height, i);
            if(dp[i]>mostWater) mostWater=dp[i];
        }
        
        return mostWater;
    }
}

findMaxArea()에서는 two-pointer approach로 파라미터로 주어진 높이값을 만족하는 양쪽 끝 수직선을 찾아 채울 수 있는 물의 양을 반환한다.
사실 이전 값을 활용하고 있진 않으므로 dp가 아닌 그냥 two-pointer approach라고 해도 무방할듯 ...

brute force보다 속도는 빨라진 것을 볼 수 있으나, 여전히 최악의 경우 O(N^2)이기에 시간 효율성은 그닥이다.

3. two-pointer approach

정말 직관적인 방법이다! 이 직관적인 방법은 아래에 쓴 재미있는 사실을 기반으로 한다.

• 채울 수 있는 물의 양은 언제나 양 끝의 수직선 중 더 짧은 수직선을 높이로 한다.
• 양 끝선이 멀어질 수록 물의 양이 증가한다.

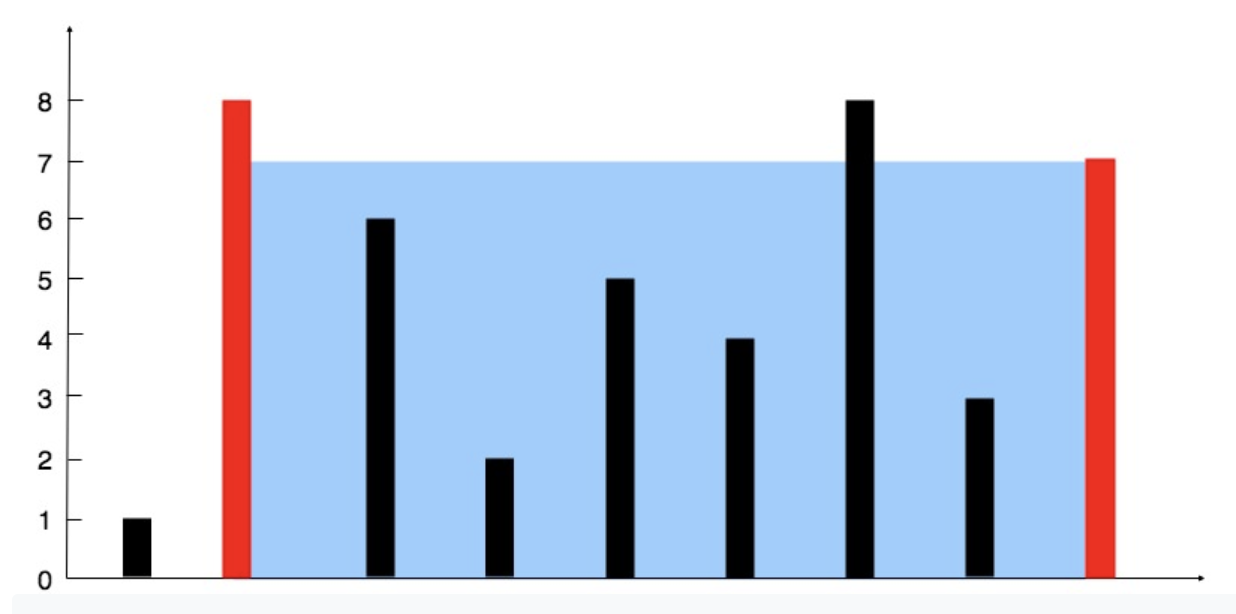
• 두 포인터를 두고, 하나는 배열의 시작, 하나는 배열의 끝을 가리키게 한다.
  → 두 포인터의 위치가 바뀌어도 넓이는 바뀌지 않으니, while (start < end) 동안 반복한다.
• maxArea변수로 지금까지의 채울 수 있는 물의 양의 최대값을 저장한다.
• 각 iteration마다, 두 포인터 중 짧은 값을 높이로 한 maxArea를 갱신한다.
• 두 포인터 중 짧은 쪽을 한 칸씩 옮기며 물을 채우는 폭을 좁혀 간다.

while (start < end) {
            maxArea = Math.max(maxArea, Math.min(height[start], height[end]) * (end - start));
            if (height[start] < height[end])
                start++;
            else
                end--;
        }
        return maxArea;

O(N)의 효율을 가져서 실행 시간이 확 줄었다.