구현
14891 톱니바퀴
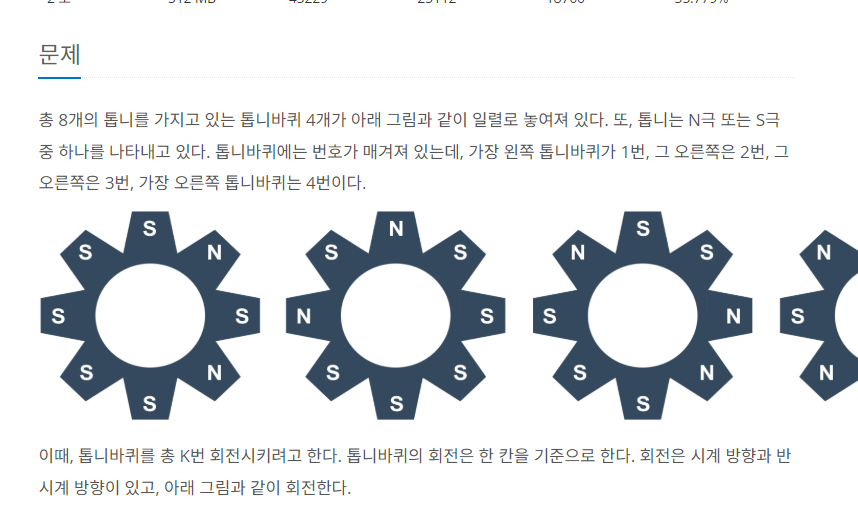

말 그대로 회전 구칙을 구현해서 풀면 될 것 같다.
from collections import deque as dq
gears = [dq(map(int, input().strip())) for _ in range(4)]
#기어 상태 입력
k = int(input())
#회전 횟수 입력
rot = [tuple(map(int, input().split())) for _ in range(k)]
#회전 명령 입력
def rotate(gear, direction):
checked = [False] * 4 #회전 여부 확인했는지
rotate_dir = [0] * 4 #회전 방향
rotate_dir[gear] = direction #초기 기어 방향 설정
checked[gear] = True #초기 기어 확인함
#왼쪽 기어 회전
for i in range(gear - 1, -1, -1):
if gears[i + 1][6] != gears[i][2]: #맞닿은 극이 다르면
rotate_dir[i] = -rotate_dir[i + 1] #반대 방향으로 회전
checked[i] = True #확인함
else:
break #극이 같으면 회전 안함
#오른쪽 기어 회전
for i in range(gear + 1, 4):
if gears[i - 1][2] != gears[i][6]: #맞닿은 극이 다르면
rotate_dir[i] = -rotate_dir[i - 1] #반대 방향으로 회전
checked[i] = True #확인함
else:
break #극이 같으면 회전 안함
#회전
for i in range(4):
if checked[i]: #확인한 기어만 회전
if rotate_dir[i] == 1: #시계 방향
gears[i].appendleft(gears[i].pop())
elif rotate_dir[i] == -1: #반시계 방향
gears[i].append(gears[i].popleft())
for gear, direction in rot:
rotate(gear - 1, direction) #기어 번호를 조정하고 회전 명령 실행
#기어 점수 계산
score = 0
for i in range(4):
if gears[i][0] == 1: #첫 번째 톱니가 N극이면
score += 2 ** i #점수 계산
print(score) #최종 점수 출력회전을 구현할 수 있도록 deque를 통해 리스트를 돌려 줬다. 회전시키는 기어가 2번이나 3번일 수도 있으니 왼쪽과 오른쪽 기어들의 회전 여부를 모두 확인하고, 회전을 실행하도록 했다.
최단 경로
11403 경로 찾기
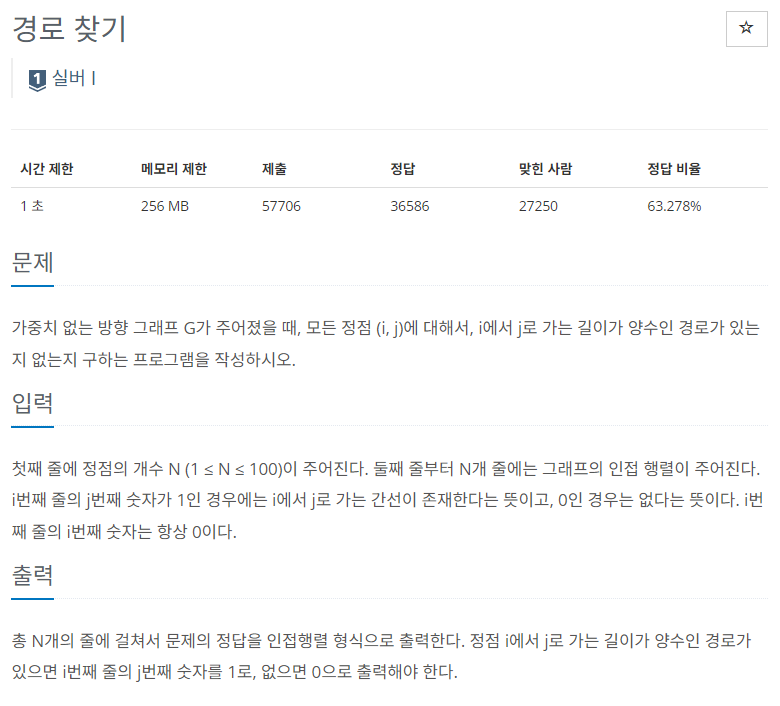
방향 그래프를 입력받고, 인접 행렬 형식으로 답을 출력해야 한다.
# n개의 줄이 주어졌을 때
n = int(input())
#인접 행렬 입력받음
adj_matrix = [list(map(int, input().split())) for _ in range(n)]
adj_matrix_res = adj_matrix # 결과를 저장할 행렬 초기화
# 모든 정점에 대해서 경로 찾기
for k in range(n):
#k라는 중간 경유지를 거쳐서 연결되어있는지 확인
for i in range(n):
for j in range(n):
if adj_matrix[i][k] and adj_matrix[k][j]: # i에서 k로 가는 경로가 있고, k에서 j로 가는 경로가 있다면
adj_matrix_res[i][j] = 1 # i에서 j로 가는 경로가 있다고 표시
# 결과 행렬 출력
for row in adj_matrix_res:
print(' '.join(map(str, row)))
처음 입력받은 것들을 바탕으로 원래는 [i][j]와 [j][i]가 둘 다 1이면 연결이겠지? 정도로 생각했다.
그런데 그냥 그걸 한번 반복하면 처음과 똑같은 결과만 나온다는 걸 깨달았고, 중간 경유지를 하나 설정해서 그 구역과의 연결 여부를 확인하면 어떨까 했다.
2660 회장뽑기

가장 직접적으로 인맥이 넓은 사람을 구하는...? 문제인 듯 하다... 친구가 없으면 회장도 못 하는 세상이다...
from collections import deque
# 회원 수
n = int(input())
friends = {i: [] for i in range(1, n+1)}
# 친구 관계를 저장할 딕셔너리 초기
# 친구 관계 입력받기
while True:
a, b = map(int, input().split())
if a!=-1 and b!=-1:
# 입력된 친구 관계가 -1이 아닐 때까지 반복
friends[a].append(b)
friends[b].append(a) # 친구 관계는 양방향이므로 양쪽 모두에 추가
else:
break
# 회원별로 점수 계산
def calc_scores(member):
visited = [False] * (n + 1)
distance = [0] * (n + 1)
queue = deque([member])
visited[member] = True
while queue:
current = queue.popleft()
for neighbor in friends[current]:
if not visited[neighbor]:
visited[neighbor] = True
distance[neighbor] = distance[current] + 1
queue.append(neighbor)
if not all(visited[1:]):
return float('inf') # 모든 회원을 방문하지 못한 경우 무한대 반환
return max(distance[1:]) # 모든 회원을 방문한 경우 최대 거리를 반환
scores = []
min_score = float('inf') # 최소 점수를 무한대로 초기화
for i in range(1, n+1):
score = calc_scores(i) # 각 회원에 대해 점수 계산
scores.append(score) # 점수를 리스트에 추가
if score < min_score: # 최소 점수 갱신
min_score = score
# 최소 점수를 가진 사람들 찾기
candidates = [i + 1 for i, s in enumerate(scores) if s == min_score]
# 출력
print(min_score, len(candidates))
print(' '.join(map(str, candidates)))결국 점수라는 건 모든 노드에 대한 최단거리 중 가장 큰 것이므로, bfs 알고리즘을 이용해 점수를 구하고 후보자를 찾도록 했다.
18352 특정 경로의 도시 찾기
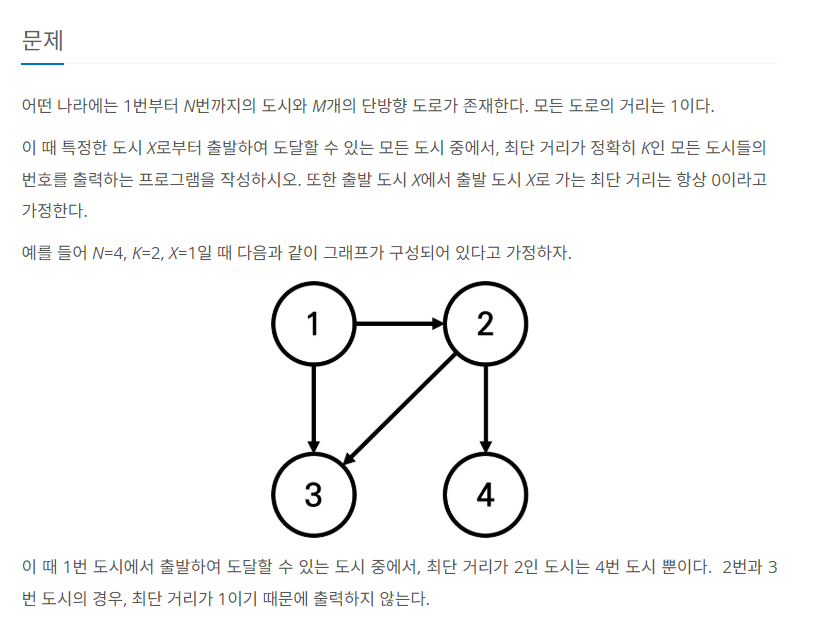
단방향 도로임에 유의해서 풀었다. 최단 거리 문제답게 deque를 이용한 bfs를 이용했다.
from collections import deque as dq
n, m, k, x = map(int, input().split())
graph = [[] for _ in range(n + 1)]
# 도로 입력(인접 리스트 형태로 저장)
for _ in range(m):
a, b = map(int, input().split())
graph[a].append(b)
# bfs 실행
distance = [-1] * (n + 1)
distance[x] = 0 # 시작 도시의 거리는 0
queue = dq([x])
while queue:
current = queue.popleft()
for neighbor in graph[current]:
if distance[neighbor] == -1: # 아직 방문하지 않은 r곳이면
distance[neighbor] = distance[current] + 1 # 거리 업데이트
queue.append(neighbor)
# k 거리인 도시 찾기
result = [i for i in range(1, n + 1) if distance[i] == k]
if result:
for city in sorted(result):
print(city)
else:
print(-1)
#없다면 -1 출력
시간 초과가 떠서 pypy3로 다시 제출하니까 괜찮았다.
1916 최소비용 구하기
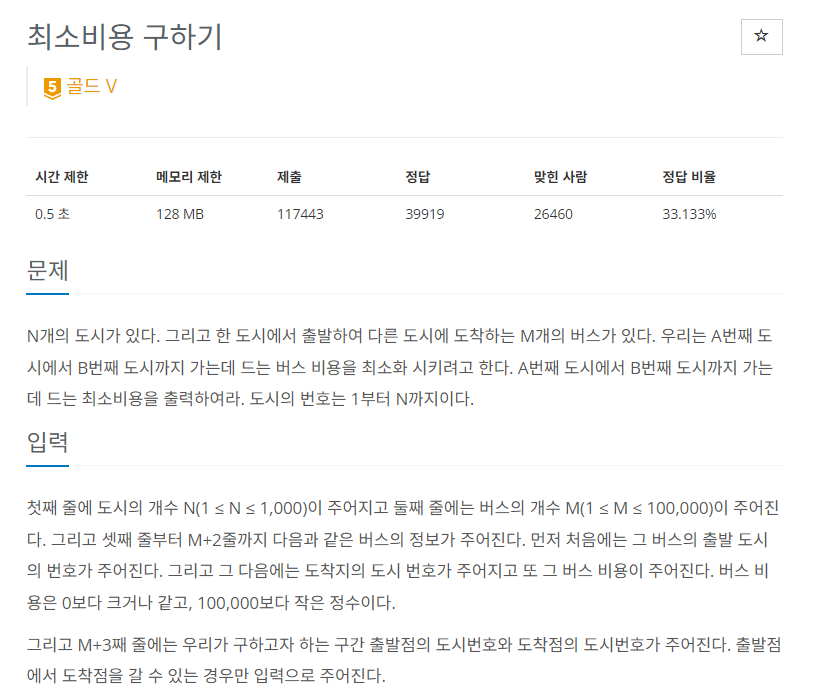
bfs 방식으로 탐색하되, 비용이 있는 리스트를 따로 만들고 그 리스트를 이용해 거리 대신 비용을 저장하면서 탐색하면 될 것 같다.
from collections import deque as dq
n = int(input())
m = int(input())
graph = [[] for _ in range(n + 1)] #인접리스트
fee = [[] for _ in range(n + 1)] # 각 버스의 요금
for i in range(m):
a, b, f = map(int, input().split())
graph[a].append(b) # a에서 b로 가는 버스
fee[a].append(f) # a에서 b로 가는 버스의 요금
start, end = map(int, input().split())
# 시작 도시와 도착 도시
# bfs 실행
distance = [-1] * (n + 1) # 각 도시까지의 최소 요금
distance[start] = 0 # 시작 도시의 요금은 0
queue = dq([start])
while queue:
current = queue.popleft()
for i in range(len(graph[current])):
neighbor = graph[current][i] # 현재 도시에서 갈 수 있는 다음 도시
cost = fee[current][i] # 현재 도시에서 다음 도시로 가는 버스의 요금
if distance[neighbor] == -1 or distance[neighbor] > distance[current] + cost:
distance[neighbor] = distance[current] + cost # 최소 요금 업데이트
queue.append(neighbor)
# 도착 도시까지의 최소 요금 출력
if distance[end] != -1:
print(distance[end])
이렇게 작성했더니 시간 초과 문제가 있어서, 다른 방식을 고민해 보았다. 문제에 나와 있는 알고리즘 분류를 보고 데이크스트라 방식으로 작성해 봤다.
from collections import deque as dq
n = int(input())
m = int(input())
graph = [[] for _ in range(n + 1)]
for i in range(m):
a, b, f = map(int, input().split())
graph[a].append((b, f)) # a에서 b로 가는 버스와 요금금
start, end = map(int, input().split())
# 시작 도시와 도착 도시
# 데이크스트라
inf = float('inf')
distance = [inf] * (n + 1)
distance[start] = 0 #시작도시는 0
queue = dq([(0, start)]) # (현재 요금, 현재 도시)
while queue:
current_cost, current_city = queue.popleft()
if current_cost > distance[current_city]:
continue # 이미 더 작은 비용으로 방문한 경우
for next_city, fare in graph[current_city]:
new_cost = current_cost + fare
if new_cost < distance[next_city]:
distance[next_city] = new_cost
queue.append((new_cost, next_city))
# 도착 도시까지의 최소 요금 출력
print(distance[end] if distance[end] != inf else -1)처음 써보는 방식이라서 알고리즘을 좀 찾아보고 기본 형태를 보고 작성했다.
그래프 이론
11725 트리의 부모 찾기
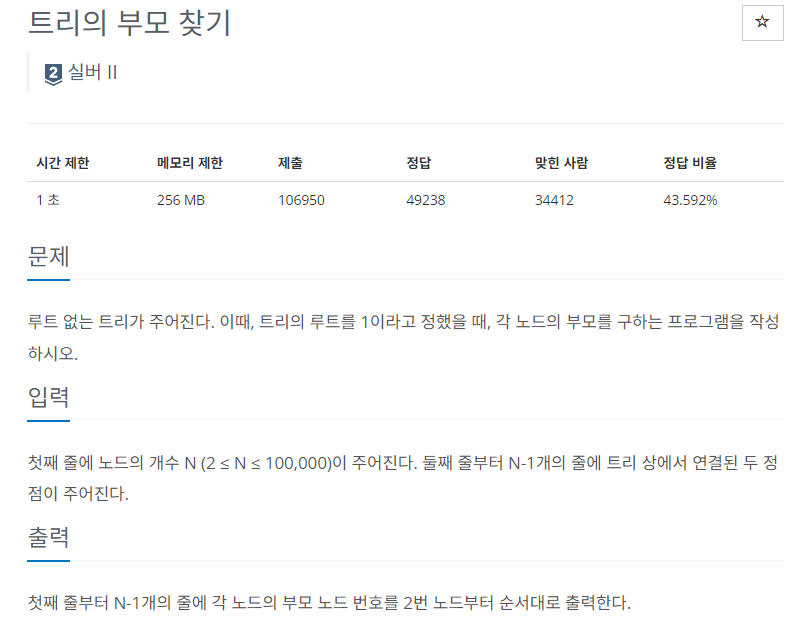
양방향 그래프로 입력을 저장하고 트리의 부모를 찾았다.
from collections import deque as dq
n = int(input())
graph = [[] for _ in range(n + 1)]
for i in range(n - 1):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
#양방향 리스트로 입력
# 부모 저장 배열
parent = [0] * (n + 1)
# BFS로 트리 탐색
queue = dq([1])
while queue:
current = queue.popleft()
for neighbor in graph[current]:
if parent[neighbor] == 0: # 아직 방문하지 않은 경우
parent[neighbor] = current
queue.append(neighbor)
for i in range(2, n + 1):
print(parent[i]) # 각 노드의 부모 노드 출력dfs로 작성했다가 메모리 문제가 있어서 bfs로 다시 작성했다.
5014 스타트 링크

그냥 멀쩡한 엘리베이터로 가던가 계단으로 가면
버튼을 최소로 누르는 것이므로 가중치가 전부 동일한 최단 거리 문제로 볼 수 있다. bfs를 이용해 풀어보기로 했다.
f, s, g, u, d = map(int, input().split())
# f: 총 층수, s: 시작 층, g: 목표 층, u: 위로 이동하는 층 수, d: 아래로 이동하는 층 수
from collections import deque as dq # deque를 사용하여 BFS 구현
def bfs(s):
visited = [False] * (f + 1) # 방문 여부를 저장하는 리스트
queue = dq([(s, 0)]) # (현재 층, 이동 횟수)
visited[s] = True # 시작 층 방문 표시
while queue:
current, moves = queue.popleft() # 현재 층과 이동 횟수 가져오기
if current == g: # 목표 층에 도달한 경우
return moves # 이동 횟수 리턴턴
# 위로 이동
up = current + u
if up <= f and not visited[up]: # 위로 이동 가능한 층인지 확인
visited[up] = True # 방문 표시
queue.append((up, moves + 1)) # 큐에 추가
# 아래로 이동
down = current - d
if down >= 1 and not visited[down]: # 아래로 이동 가능한 층인지 확인
visited[down] = True # 방문 표시
queue.append((down, moves + 1)) # 큐에 추가
return -1 # 목표 층에 도달할 수 없는 경우 -1 반환
result = bfs(s) # BFS 실행
if result == -1:
print("use the stairs") # 목표 층에 도달할 수 없는 경우
else:
print(result)도달이 불가능한 경우도 있으므로 return -1을 추가하기 위해서 bfs를 함수로 정의해서 사용했다.
14940 쉬운 최단거리
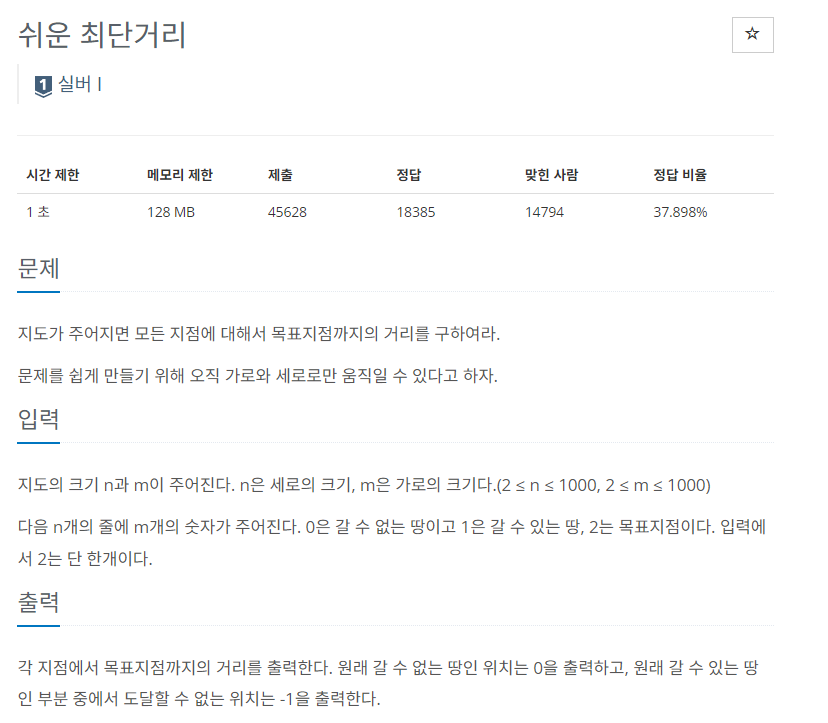
bfs로 가중치가 전부 동일한 상태에서 최단 거리를 구하고자 했다.
n, m = map(int, input().split())
#지도 크기
import sys
map = [list(map(int, sys.stdin.readline().strip().split())) for _ in range(n)]
#지도 입력 받기
# 결과 배열: -1로 초기화 (나중에 0과 구분 위해)
distance = [[-1] * m for _ in range(n)]
# target 찾기
for i in range(n):
for j in range(m):
if map[i][j] == 2:
target = (i, j)
break
# BFS를 위한 큐 초기화
from collections import deque
queue = deque()
queue.append(target)
distance[target[0]][target[1]] = 0 # 시작 위치의 거리는 0
#4방향 이동 추가
dx = [1, -1, 0, 0]
dy = [0, 0, 1, -1]
while queue:
x, y = queue.popleft() # 현재 위치
for i in range(4): # 4방향 탐색
nx = x + dx[i]
ny = y + dy[i]
# 범위 체크 및 이동 가능 여부 확인
if 0 <= nx < n and 0 <= ny < m and map[nx][ny] == 1 and distance[nx][ny] == -1:
distance[nx][ny] = distance[x][y] + 1 # 거리 업데이트
queue.append((nx, ny)) # 큐에 추가
# 결과 출력
for i in range(n):
for j in range(m):
if map[i][j] == 0:
print(0, end=' ') # 원래 갈 수 없는 곳
elif distance[i][j] == -1:
print(-1, end=' ') # 갈 수 있었지만 도달 못한 곳
else:
print(distance[i][j], end=' ') # 이동 가능한 경우 거리 출력
print() # 줄바꿈bfs로 탐색하고 결과를 출력해 준다.
15723 n단 논법
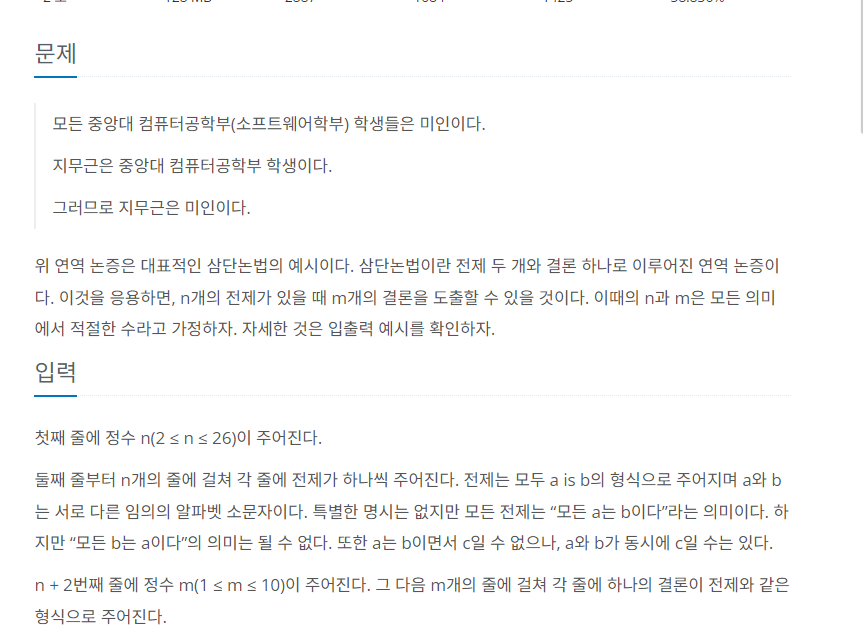
n = int(input())
graph = [[False] * 26 for _ in range(26)]
# a > B라면 graph[a][b] = True
for i in range(n):
a, _, b = input().split() # a is b
ai = ord(a) - ord('a')
bi = ord(b) - ord('a')
graph[ai][bi] = True
for k in range(26):
for i in range(26):
for j in range(26):
if graph[i][k] and graph[k][j]:
graph[i][j] = True
#결론 판별
m = int(input())
for _ in range(m):
a, _, b = input().split()
ai = ord(a) - ord('a')
bi = ord(b) - ord('a')
print('T' if graph[ai][bi] else 'F')경로 찾기 문제와 동일한 방식을 이용했다.