Notion에서 작성한 글이라, 여기에서 더 깔끔하게 보실 수 있습니다! 😮😊

---

[Challenger] 사자와 토끼

[사자와 토끼]

접근 과정

문제를 읽으며 메모한 내용

1. $N$개의 수풀, $M$개의 오솔길
   1. 오솔길은 서로 다른 두 수풀을 양방향으로 연결한다 ⇒ 무방향 그래프(Undirected Graph)
   2. 어떤 수풀에서 다른 수풀까지 1개 이상의 오솔길을 통하면 반드시 도달할 수 있다 ⇒ 연결 그래프(Connected Graph)
   3. 수풀은 정점, 오솔길은 간선
2. 사자와 토끼의 초기 위치는 같을 수 없다.
3. 매 턴마다 오솔길 1개를 따라 이동해야 한다. 이동하지 않을 수는 없다.
4. 이동한 후, 사자와 토끼가 같은 수풀에 있다면 게임이 끝난다.
   • 같은 오솔길을 통해 이동하여도 서로 다른 수풀에 도착했다면 (오솔길에서 마주친 것처럼 보이지만, 오솔길 위에서는 안타까운 일이 일어나지 않는다…) 게임이 끝나지 않는다.
5. 어떻게 움직여도 영원히 게임이 끝나지 않는 경우의 수

• ‘심지어 두 플레이어가 서로의 위치를 알고 일부러 게임을 끝내려고 해도 끝낼 수 없다!’ 라는 문제의 설명이 풀이를 생각해내는 데에 정말 큰 도움이 되었다. 그리고 한 편으론 뭔가 너무 안타까웠다. 만나고 싶어도 만날 수가 없는 사이라니… 갑자기 감성에 잠깐 젖었었다,,, 😢 요새 좀 T가 되어가는 줄 알았는데 아직 멀었나 보다.

• 사실 바로 감이 오질 않아서 예제들의 그래프를 직접 그려보면서 생각했다. 어느 상황에서 둘은 만나고 싶어도 못 만나는지를 살펴보니, 크게 세 가지 경우로 나눌 수 있었다. (설명의 편의상 ‘어떻게 움직여도 영원히 게임이 끝나는/끝나지 않는’을 ‘게임이 끝나는/끝나지 않는’으로 줄여서 작성하겠다!)

  • 두 정점(토끼가 위치한 수풀, 사자가 위치한 수풀) 사이의 최단거리가 짝수라면 게임이 끝나고, (그냥 만나버리면 된다)
  • 최단거리가 홀수일 때에도 cycle이 홀수면 게임이 끝나지만,
  • cycle이 짝수라면 게임이 끝나질 않는다.

• 두 정점 사이의 최단거리가 짝수라면 게임이 끝난다는 점은 직관적으로 이해하기 쉽다. 중요한 것은 게임을 끝낼 수 있는지의 여부기 때문에, 복잡한 경우를 생각할 것 없이 당장 최단거리로 만나버리면 게임을 끝낼 수 있다.

• 홀수일 경우엔, 삼각형과 사각형 형태의 그래프를 그려놓고 생각하면 쉽다.

  

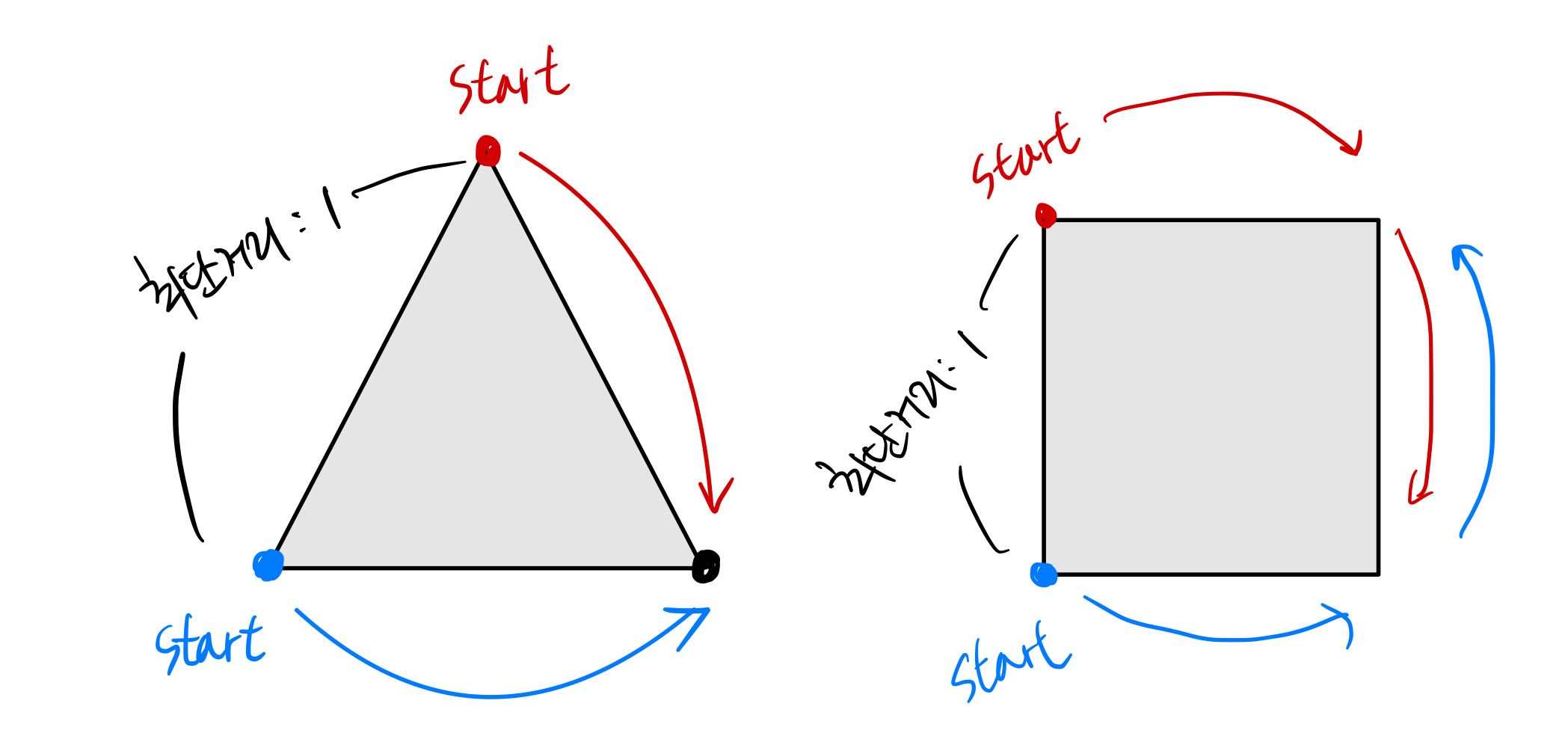
  • 두 그림 모두 두 정점 사이의 최단거리는 홀수($1$)이다. 하지만, 삼각형 형태의 그래프에서의 cycle은 $3$이고, 사각형 형태의 그래프에서의 cycle은 $4$이다.
    • 최단경로로 이동하지 않고, 굳이 우회경로로 이동하면 홀수 cycle에서는 만나려면야 만날 수가 있게 되고,
    • 짝수 cycle에서는 여전히 만날래야 만날 수가 없게 된다.

• 위와 같이 단순한 형태의 그래프면 구하기 쉽지만, 복잡한 형태의 그래프에서 수없이 많은 cycle이 있을텐데 이걸 어떻게 하나하나 다 체크하지…? 어떻게 체크해낸다고 해도 정점과 간선의 수가 많아서 제한시간 내에는 처리할 수 없어보였다. 게다가 두 정점들 사이의 거리는 각각 모두 계산해주어야 하나? $n(n-1)/2$?? 제한시간 내에는 절대 불가능해보였다.

• 삼각형 모양의 그림을 통해 천천히 생각해 보았다. 임의의 정점부터 시작하여 다른 정점들 사이의 거리를 구하기 위한 BFS를 돌린다.

  • 기존의 최단거리를 구하는 BFS는 방문하지 않은 정점에 대해서만 BFS를 이어나가고, 거리를 마킹하기 위한 작업 등을 수행하지만,
  • 여기에서는 이미 방문한 정점에 대해서도 생각해 주어야 한다. 이미 방문한 정점에 도달했을 때, 그 정점에 마킹된 최단거리가 홀수이고, 갱신하려는 거리(이를 우회경로로 이동하는 상황으로 볼 수 있다)가 짝수인 경우가 바로 홀수 cycle을 갖는 경우이다. (최단거리 $1$ + 우회한 거리 $2$ = $3$)

• 이를 종합하면 위에서 막막했던 부분들이 풀린다.

  • cycle 판단 : 이미 최단거리가 마킹된 정점에 다시 방문했는데, 갱신하려는 거리가 짝수인 경우 - 게임이 끝나는 경우이므로 $0$을 return
  • 각 정점 사이의 거리 :
    • 위의 생각들을 바탕으로, 게임이 끝나지 않는 (사자의 초기 위치, 토끼의 초기 위치) 조합은 정점 사이의 거리가 (홀수, 짝수)인 경우, (짝수, 홀수)인 경우만 존재할 수 있다. ((홀수, 홀수) 또는 (짝수, 짝수)의 경우 두 정점 사이의 최단거리가 짝수이기 때문에 게임이 끝난다.)
    • 따라서 임의의 정점부터 BFS를 돌려서, 최단거리가 홀수인 정점, 짝수인 정점의 개수만 체크해주면 된다.

Solution 1. $O(V+E)$

import sys
input = sys.stdin.readline
from collections import deque

def bfs(v):
    queue = deque([v])
    visited = [False]*(n+1)
    visited[v] = True
    distance = [0]*(n+1)
    odds = 0
    evens = 1
    
    while queue:
        cur = queue.popleft()
        for nxt in adj[cur]:
            if not visited[nxt]:
                visited[nxt] = True
                distance[nxt] = distance[cur]+1
                if distance[nxt]%2: odds += 1
                else: evens += 1
                queue.append(nxt)
            
            elif distance[nxt]%2 != (distance[cur]+1)%2: return 0
    
    return odds*evens*2

n, m = map(int, input().split())
adj = [[] for _ in range(n+1)]
for _ in range(m):
    u, v = map(int, input().split())
    adj[u].append(v)
    adj[v].append(u)

print(bfs(1))

• 위의 생각을 그대로 구현한 풀이이다. 거리가 $0$이라고 볼 수 있는 첫 번째 정점도 포함시켜야 하므로, evens는 1로 시작한다.
• 기존 최단거리 BFS와 동일하게, 최단거리를 갱신할 수 있는 정점에 대해서는 최단거리를 갱신하고, 갱신한 최단거리가 홀수인지, 짝수인지 체크하여 각각 개수를 세어준다.
  • 이미 방문한 정점에 대해서는, 최단거리와 우회거리의 홀짝성이 다를 경우 $0$을 return한다.

Solution 1-2. $O(V+E)$

import sys
input = sys.stdin.readline
from collections import deque

def bfs(v):
    queue = deque([v])
    state = [None] * (n+1) 
    state[v] = False
    evens = 1
    
    while queue:
        cur = queue.popleft()
        for nxt in adj[cur]:
            if state[nxt] is None:
                state[nxt] = not state[cur]
                if not state[nxt]: evens += 1
                queue.append(nxt)

            elif state[nxt] == state[cur]: return 0
    
    return evens*(n-evens)*2

n, m = map(int, input().split())
adj = [[] for _ in range(n+1)]
for _ in range(m):
    u, v = map(int, input().split())
    adj[u].append(v)
    adj[v].append(u)

print(bfs(1))

• Solution 1.과 로직상의 차이는 없다. 중요한 것은 홀짝성이며, 가중치가 없는 그래프이므로 두 정점 사이의 거리는 항상 $1$이기 때문에 다른 정점으로 이동할 때의 거리는 항상 홀수 → 짝수 → 홀수 → 짝수, … 의 형태로 증가하므로 True / False로 관리할 수 있겠다고 생각했다.
• 이에 더하여, visited 또한 None으로 처리하면 방문 여부 체크와 최단거리 체크까지 한 번에 묶어서 할 수 있겠다는 생각이 들었다.
• 홀수인 정점의 수는 $N-|V_{even}|$ 이므로, 각각에 대해서 세지 않고 짝수인 경우에만 세어준다.
• 갱신하려는 거리(우회했을 때의 거리)는 현재 정점까지의 최단거리 $+1$(T/F 반전)이므로, 홀짝성이 바뀐다는 점을 생각하면 굳이 True / False를 반전시키지 않고 현재의 홀짝성만 체크해주어도 된다.
• 이를 통해 상수 시간들을 조금 줄였고, 메모리 소비 또한 줄일 수 있었다.

---

Memo

• 태그를 보니 ‘이분 그래프’가 있었다. 이분 그래프가 뭔지 찾아보고 문제도 풀어보아야 겠다.