Notion에서 작성한 글이라, 여기에서 더 깔끔하게 보실 수 있습니다! 😮😊
[Challenger] 조이스틱
접근 과정
- 각 알파벳을
'A'에서 원하는 알파벳으로 바꿔주는 ▲, ▼ 조작 횟수는 커서의 이동과 독립적(커서를 어떤 식으로 이동하더라도 알파벳을 바꾸는 조작 횟수는 변하지 않음)임을 생각하면, 문제가 다음과 같이 핵심만 남게 된다.- 주어진 이름으로 변경하기 위한 커서 이동의 최소 횟수
- 즉,
'A'를 제외한 다른 모든 알파벳을 순회하기 위한 커서 이동의 최소 횟수
커서 이동의 최소 횟수
- 크게 네 가지 경우를 생각해볼 수 있다.
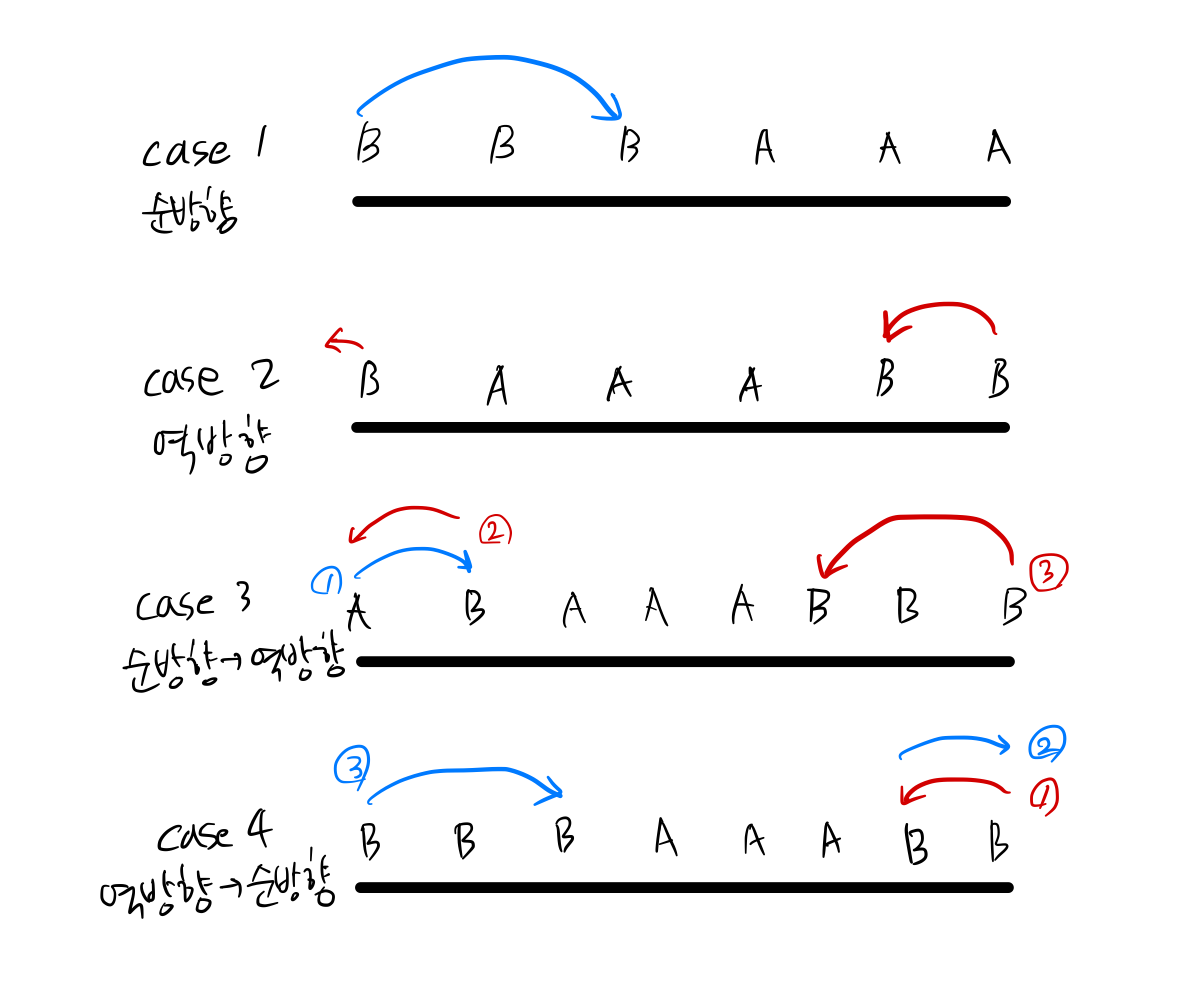
- 순방향으로만 이동하는 것이 최소인 경우
- 역방향으로만 이동하는 것이 최소인 경우
- 순방향으로 이동했다가 역방향으로 이동하는 것이 최소인 경우
- 역방향으로 이동했다가 순방향으로 이동하는 것이 최소인 경우
-
이를 두 가지 경우로 압축할 수 있다.
- 순방향으로만 이동하는 것이 최소인 경우
- case 4(역방향으로 이동했다가 순방향으로 이동하는 경우)에서, 역방향 이동 부분을 제외한 것과 동일한 상황이다.
- 역방향으로만 이동하는 것이 최소인 경우
- case 3(순방향으로 이동했다가 역방향으로 이동하는 경우)에서, 순방향 이동 부분을 제외한 것과 동일한 상황이다.
- 순방향으로만 이동하는 것이 최소인 경우
-
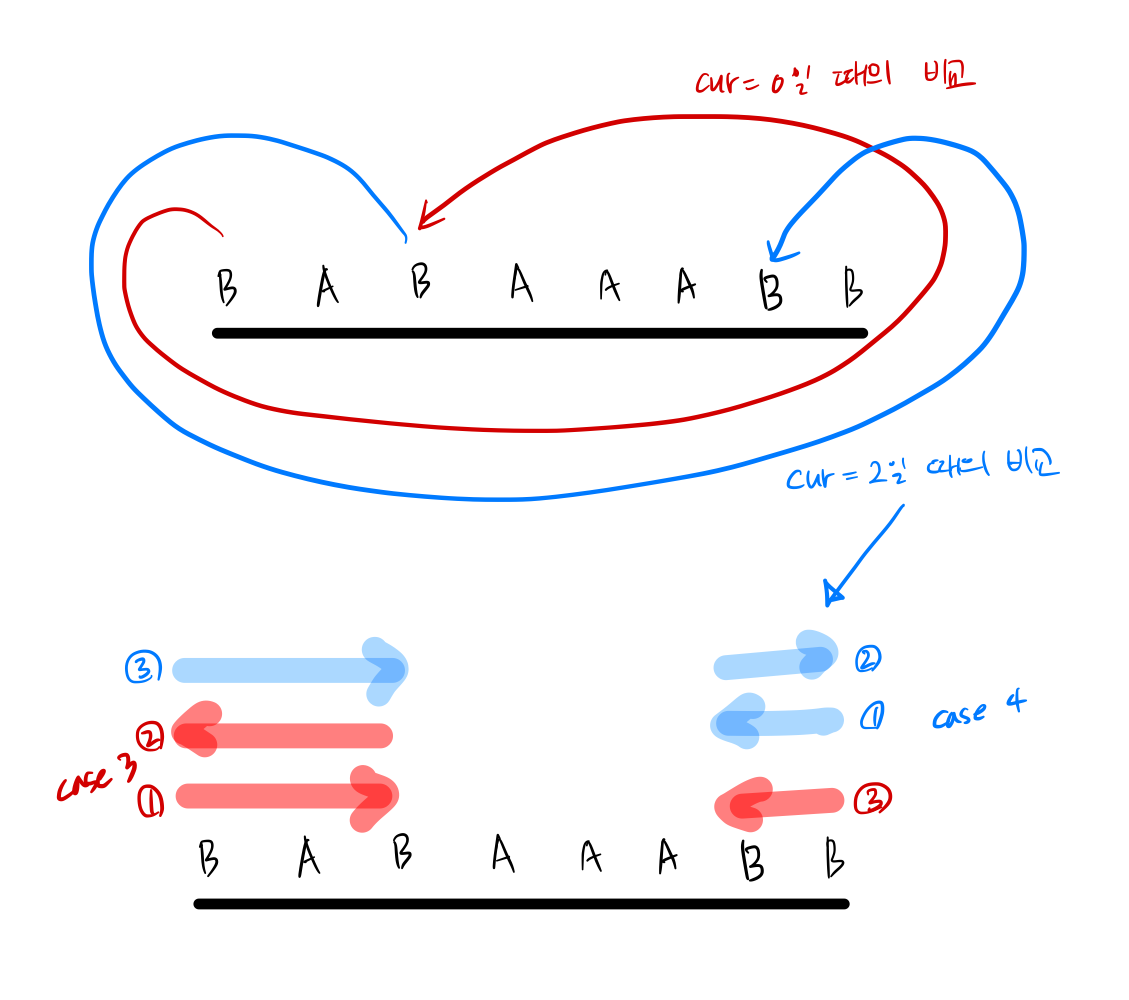
이를 어떻게 구현할지 생각해 보면, 일단 순방향으로 순회하면서, 현재 위치 기준으로 다음에 나오는
'A'가 아닌 인덱스를 찾는다. -
그 다음 두 방법 중 어떤 방법으로 이동하는 것이 최소 이동인지 계속해서 비교해 나가며 커서 이동 횟수의 최솟값을 갱신한다.
Solution 1.
def solution(name):
n = len(name)
ud = sum(min(ord(c)-65, 91-ord(c)) for c in name)
lr = n-1
for cur in range(n):
nxt = cur+1
while nxt < n and name[nxt] == 'A': nxt += 1
lr = min(lr, 2*cur+(n-nxt), cur+2*(n-nxt))
return ud+lr- 그대로 구현한 풀이이다. 커서의 최대 이동 횟수는 단순히 순방향으로 모든 알파벳에 대해 순회할 때의 이동 횟수이므로, 초기값을
len(name)-1로 설정한다.
Solution 2.
def solution(name):
n = len(name)
ud = 0
lr = n-1
for cur in range(n):
if name[cur] != 'A' or cur == 0:
ud += min(ord(name[cur])-65, 91-ord(name[cur]))
nxt = cur+1
while nxt < n and name[nxt] == 'A': nxt += 1
lr = min(lr, 2*cur+(n-nxt), cur+2*(n-nxt))
return ud+lr- 다음 두 가지를 생각하여 개선한 풀이이다.
- 현재 위치(
cur)의 문자가'A'가 아닐 때만 이동 경로 최적화의 여지가 생긴다.'JAN'과'JAAAAAAAAN'을 생각해 보면, 이 둘의 커서 이동 횟수는 같다.- 하지만 Solution 1.은
'JAAAAAAAAN'에서cur=1다음으로 오는'A'가 아닌 글자를 찾기 위해 8번의 순회,cur=2다음으로 오는'A'가 아닌 글자를 찾기 위해 7번의 순회, … 로 커서 이동 횟수 최소화의 여지가 없는 불필요한 순회를 계속 진행하게 된다. - 이를 현재 위치의 문자가
'A'가 아닐 때에만 갱신을 시도하는 방법으로 시간복잡도를 선형 시간으로 바꿀 수 있게 된다. - 하지만 주의해야 할 부분이 있다.
'AAAAB'와 같은 경우 갱신이 맨 마지막에만 이루어져 case 2와 같이 단순히 역방향으로만 이동하는 것이 최소인 경우가 제대로 계산되지 않는다.- 첫 번째 알파벳(
cur=0)에 대해 일단 계산해주고 시작하면 단순히 순/역방향으로만 이동하는 것이 최소인 경우를 포함시킬 수 있다.
- 첫 번째 알파벳(
- ▲, ▼ 조작은 커서의 이동과 독립적이라고 따로 계산해 놓을 것이 아니라, 어차피 모든 알파벳에 대해 순회하므로 이 때 같이 계산해준다.
Solution 3.
def solution(name):
table = {'A':0, 'B':1, 'C':2, 'D':3, 'E':4, 'F':5, 'G':6, 'H':7, 'I':8, 'J':9, 'K':10, 'L':11, 'M':12, 'N':13, 'O':12, 'P':11, 'Q':10, 'R':9, 'S':8, 'T':7, 'U':6, 'V':5, 'W':4, 'X':3, 'Y':2,'Z':1}
ud = table[name[0]]
n = len(name)
last = 0
lr = n-1
for cur in range(1, n):
if name[cur] != 'A':
ud += table[name[cur]]
lr = min(lr, 2*last + n-cur, last + 2*(n-cur))
last = cur
lr = min(last, lr)
return ud + lr- Solution 2. 를 반대로 생각한 풀이이다.
'A'가 아닌 이전의 마지막 알파벳(최근에 수정한 마지막 알파벳)의 인덱스로 계산해 주면, 다음에 등장하는'A'이외의 다른 알파벳을 찾기 위한while문이 필요가 없어진다. i.e.,- Solution 2. 는 현재 위치와 이후에 나올 위치를 비교하는 방법이고,
- 이 방법은 이전에 나왔던 위치와 현재 위치를 비교하는 방법이다.
- case 1과 같이 단순히 순방향으로 이동하는 것이 최소인 경우를 처리해주기 위해, 모든 알파벳에 대해 순회를 마친 뒤의
last는 순방향으로 커서를 이동하는 횟수와 동일하므로 비교한 뒤 합하여 return해준다.
- 기존의 ▲, ▼ 조작 횟수는
ord()두 번,min()한 번으로 세 번의 함수를 호출하지만, 각 알파벳에 대해 조작 횟수를 딕셔너리에 매핑해 놓으면, 매번 Amortized 에 값을 누적할 수 있게 된다.