Notion에서 작성한 글이라, 여기에서 더 깔끔하게 보실 수 있습니다! 😮😊

---

[Challenger] 공 이동 시뮬레이션 (아직 못 품)

[공 이동 시뮬레이션]

접근 과정

• 문제를 처음 읽고 나서, 격자 바깥으로 공이 이동하려는 경우를 잘 신경써줘야 할 것 같다고 생각했다.

접근 1. $O(Q(NM))$

• $1 \le n \le 10^9$ 이고 $1 \le m \le 10^9$인데다가 $1 \le Q \le 200000$이기 때문에 무조건 무조건 TLE가 날 수밖에 없는 풀이지만 마땅한 구현이 떠오르지 않아 일단 시간복잡도를 고려하지 않고 짠 다음에, 단계적으로 쥐어짜나가야겠다고 생각했다.
• (편의상 $grid[i][j]$에서, $i =0$ 또는 $i=n-1$, $j=0$ 또는 $j = n-1$인 경우를 벽에 닿는 경우라고 표현하였습니다.)
• 먼저 격자의 모든 칸을 $1$로 초기화한다(물론 이 과정만 해도 TLE가 난다). 이후 각 쿼리를 수행하며 벽에 닿는 칸들에 대해서는 벽에 닿을 때마다 1씩 증가시켜주고, 반대편의 벽과 멀어지는 칸에 대해서는 한 줄씩 $0$으로 바꿔준다.
• 이를 반복하여 쿼리를 모두 수행하면 $[x][y]$에 시작점의 개수가 남는다.

접근 2. $O(Q(N+M))$

• 위 방식에서 개선했다. $\Delta x$, $\Delta y$ 쿼리는 서로 독립적임을 생각하면, $nm$칸에 대해 모두 그 값을 갱신해줄 것이 아니라,
• $n\times 1$칸에는 $\Delta y$ 쿼리를 적용하고, $1 \times m$칸에는 $\Delta x$ 쿼리를 적용한 다음 $row[x] \times col[y]$의 값을 계산하면 $[x][y]$에 도착하는 시작점의 개수를 구할 수 있게 된다.

접근중(?)

• 격자의 상, 하, 좌, 우 끝 부분($[0][0], [0][m-1], [n-1][0], [n-1][m-1]$만 고려해주면 어떤 쿼리가 와도 칸의 값은 직사각형의 또다른 격자 형태로 남게 된다.

• 쿼리를 수행하며 공이 존재할 수 있는 부분을 ‘유효한 격자’ 라고 하자. 값의 변화는 유효한 격자의 테두리인 상, 하, 좌, 우 끝 부분에서만 일어난다. 따라서 유효한 격자의 테두리 부분은 그 값이 $1$ 이상이고, 내부는 $1$이다. 유효한 격자의 크기에 따라 $i \le 2$ 또는 $j \le 2$인 경우 내부가 존재하지 않는다.

• 다음 표와 같은 형태일 것이라 추론했다.
  

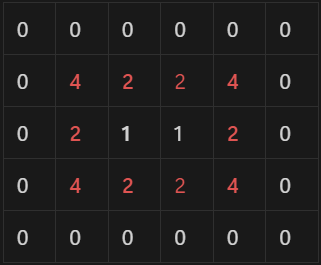
• 여기에서 어떻게 좀 잘 틀어서 생각하면 $O(Q)$에 될 것 같은데 음 음~~

(아직 못 풀었따)

def solution(n, m, x, y, queries):

		return 0

---