Notion에서 작성한 글이라, 여기에서 더 깔끔하게 보실 수 있습니다! 😮😊

---

[Challenger] 아이템 줍기

[아이템 줍기]

문제의 핵심은 특정 정점에서 시작해서 목표 정점까지의 최단거리를 구하는 BFS 문제이다. 하지만 여기서 몇몇 부분을 고려해주어야 하는데, 이 포인트들을 정리하면 다음과 같다.

Point 1. 다각형 모양의 지형을 어떻게 코드로 나타낼 수 있을지

• 많이 풀어본 격자 형태의 BFS/DFS 문제들은 $n \times m$ 의 행렬 형태로 그 값들이 주어졌으나, 이 문제는 그러한 입력이 주어지지 않는다.
• 문제에서 직사각형들의 좌표가 주어지므로, 격자 형태의 2차원 리스트를 0으로 초기화시켜서 그 좌표들을 이용하여 반복문으로 테두리에 해당하는 부분을 마킹해주면 된다.
  • 이 때, 지형의 전체 크기를 입력을 통해서 특정할 수 없으므로, 제한사항을 참고하여 $50 \times 50$의 2차원 리스트를 만들어 주면 된다. 하지만 좌표값은 $1$ 이상 $50$ 이하이므로, $51 \times 51$의 리스트를 만들어 주면 깔끔하게 처리할 수 있다.

Point 2. 다각형의 가장 바깥쪽 테두리를 통해서만 캐릭터가 이동할 수 있는데, 바깥쪽 테두리를 어떻게 식별할지

• 위 방법대로 테두리를 마킹하고 나면 다음과 같은 형태가 되어, 캐릭터는 다각형의 둘레(가장 바깥쪽 테두리)를 따라서만 이동해야 하지만, BFS 도중 다각형의 안쪽으로도 이동해버리는 경우가 생긴다(빨간 화살표).
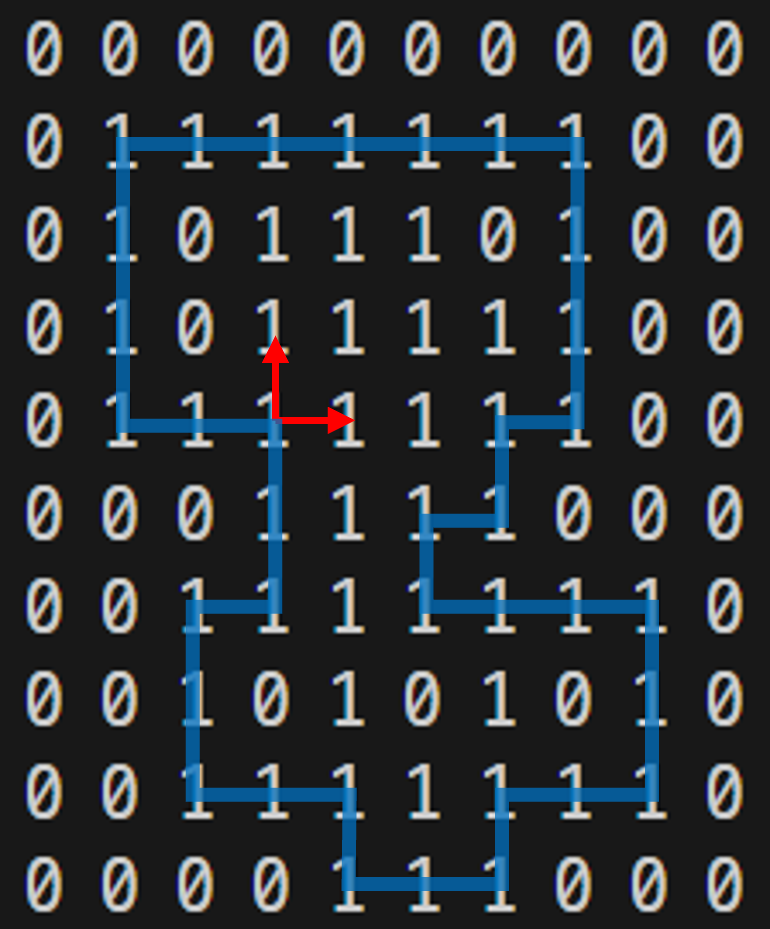
• 이를 해결하기 위한 두 가지 방법을 떠올렸는데,

1. 첫 번째 방법은 18일차 챌린저 문제였던 BOJ 5547. 일루미네이션, 그리고 개인적으로 풀었던 BOJ 2573. 빙산 문제에서처럼, 테두리를 0으로 두르고 BFS/DFS를 돌려서 가장 바깥쪽 테두리를 식별하는 방법,
2. 두 번째 방법은 직사각형의 좌표를 이용하여 격자에 마킹을 할 때, 테두리가 아닌 내부에 대해 테두리와 다른 값으로 마킹해놓고, 그 다음 직사각형의 좌표를 이용하여 마킹할 때 내부에 해당하는 값이 이미 마킹되어있다는 것은 다각형의 내부에 해당하므로 여기에는 마킹하지 않는 방법이다.
   • 이 방법이 가능한 이유는, 서로 다른 두 직사각형이 꼭짓점에서 만나거나, 변이 겹치는 경우는 없고, 한 직사각형이 다른 직사각형 안에 완전히 포함되는 경우가 없다고 했기 때문에 가능하다. 만약 이러한 경우가 있었다면 겹치는 부분은 테두리와 내부를 구분할 수 없으므로 다른 방법을 이용해야 한다.

• 첫 번째 방법은, 가장 바깥쪽 테두리를 식별하는 데 $O((n+1)^2)$ 의 시간이 걸린다. $0$을 가로와 세로에 한 줄씩 더 붙여줘야 하므로 메모리를 조금 더 사용하기도 한다.
• 두 번째 방법은, 제한사항과 문제 설명을 통해 최악의 경우를 떠올려 보면 네 개의 직사각형이 서로 꼭짓점이나 변이 겹치지 않는 가장 큰 경우인데(’+’ 모양), 이 경우 $O(4(n-2)^2)$ 의 시간이 걸린다.
• 당장 두 번째 방법이 구현하기에 쉬워 보여 일단 이 방법으로 코드를 짜긴 했는데, 첫 번째 방법도 추후 시도해보아야 겠다.

Point 3. 변의 길이가 1인 ‘ㄷ’자 모양의 경우 마치 ‘ㅁ’처럼 마킹되는 문제를 어떻게 해결할지

• 위 그림을 통해서도 볼 수 있는 문제이다. 문제가 되는 부분만 나타내 보면 다음과 같다.
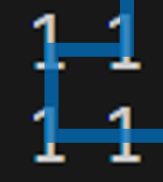
• 실제로는 ‘ㄷ’자 형태로 돌아서 이동해야 하지만, ‘ㅁ’자 형태로 나타내어진다. 따라서 최단 경로 탐색 시 ‘ㄷ’자로 돌아서 이동하는 것이 아닌 ‘ㅣ’ 자로 (최단 경로로) 이동해버려 잘못된 거리를 계산하게 되는 문제가 발생한다.
• 이를 해결하기 위해, 좌표를 두 배로 늘려서 마킹을 하면 이 사이에 빈 공간이 생기기 때문에 아주 깔끔하게 해결할 수 있다. 단, BFS 시작 좌표와 아이템의 좌표에도 2를 곱해주어야 하고, 거리 계산 시에도 이를 유의해야 한다.
• 이를 이용하면 격자가 다음과 같은 형태로 아주 깔끔하게 나타내어진다.

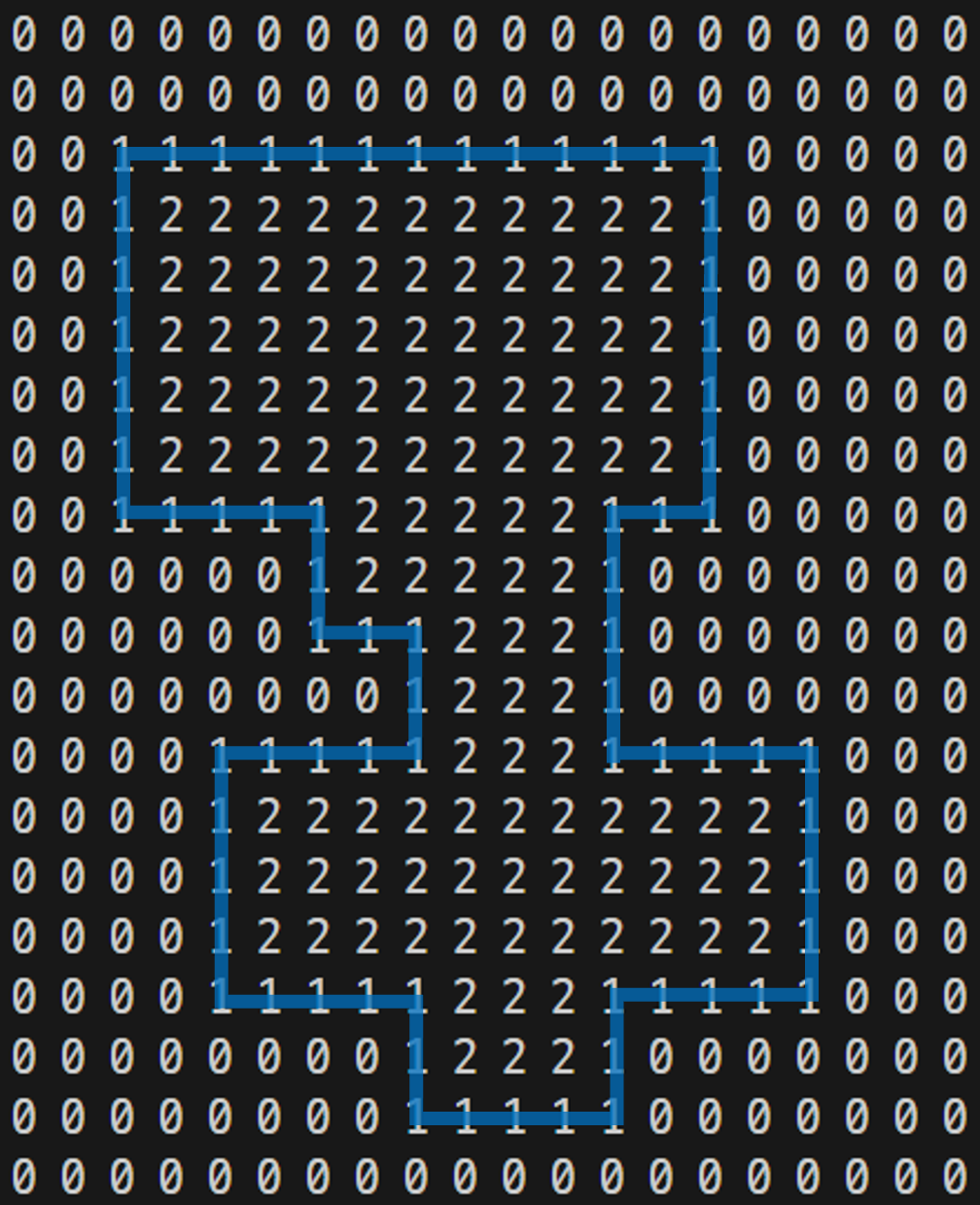
Solution. $O(n^2)$

from collections import deque

def bfs(tp, i, j, itemX, itemY):
    queue = deque([(i, j)])
    delta = ((-1, 0), (1, 0), (0, -1), (0, 1))
    visited = [[0]*102 for _ in range(102)]
    visited[i][j] = 1
    
    while queue:
        y, x = queue.popleft()
        for dy, dx in delta:
            ny, nx = y+dy, x+dx
            if 0<=ny<102 and 0<=nx<102 and tp[ny][nx] == 1 and not visited[ny][nx]:
                visited[ny][nx] = visited[y][x]+1
                if ny == itemY and nx == itemX: return visited[y][x]
                queue.append((ny, nx))

def solution(rectangle, characterX, characterY, itemX, itemY):
    tp = [[0]*102 for _ in range(102)]
    
    for r in rectangle:
        lx, ly, rx, ry = r
        for i in range(ly*2, ry*2+1):
            if tp[i][lx*2] != -1: tp[i][lx*2] = 1 
            if tp[i][rx*2] != -1: tp[i][rx*2] = 1
        for j in range(lx*2, rx*2+1):
            if tp[ly*2][j] != -1: tp[ly*2][j] = 1
            if tp[ry*2][j] != -1: tp[ry*2][j] = 1
        for i in range(ly*2+1, ry*2):
            for j in range(lx*2+1, rx*2):
                tp[i][j] = -1

    return bfs(tp, characterY*2, characterX*2, itemX*2, itemY*2)//2

• visited가 0일 땐 방문하지 않은 정점, 0이 아닐 땐 거리에 해당하는 값을 가지도록 했다. 기존 격자에 적절한 값으로 마킹한다면 visited 없이도 가능할 수도 있겠다는 생각이 들었는데, 일단 발표 세션 시작 전에 빠르게 정답 코드를 짜기 위해 visited를 이용했다.
• 직사각형들을 2차원 리스트에 마킹하는 과정 또한 더 가독성 좋게 바꿔볼 수 있어 보인다. 처음엔 직사각형의 모든 테두리에 대해서 내/외부 구분 없이 1로 마킹했다가 내/외부 구분을 위해 코드를 덧붙이다 보니 위와 같이 짰었다.

---

Memo

• 누적된 수면 부족과,,, 약간의 감기기운까지 있는 바람에 오늘 컨디션이 너무 안 좋아서 코드 리팩터링은 미뤄뒀다. 일단 오늘 푹 쉬고, 내일 SQLD 공부한 다음 모레 시험을 잘 봐야 겠다.