Notion에서 작성한 글이라, 여기에서 더 깔끔하게 보실 수 있습니다! 😮😊

---

[Challenger] 도둑질

[도둑질]

접근 과정

• 집들이 동그랗게 배치되어 있으므로 첫 번째 집과 마지막 집이 인접해 있다는 것을 상태 전이에 어떻게 반영해야 할지 바로 생각이 안 나서, 일단 첫 번째 집과 마지막 집이 인접하지 않았다고 가정하고 문제에 대해 생각해 보았다.
• [BOJ 2579. 계단 오르기], [BOJ 2156. 포도주 시식] 과 유사한 방식으로 점화식을 짤 수 있다.

첫 번째 집, 마지막 집 인접하지 않았다고 가정

• $dp[i][0]$을 $i$번째 집까지 털었을 때 $i$번째 집을 털지 않고 훔칠 수 있는 돈의 최댓값, $dp[i][1]$을 $i$번째 집까지 털었을 때 $i$번째 집을 털고 훔칠 수 있는 돈의 최댓값이라 하자. 점화식은 다음과 같이 나타낼 수 있다.

  $dp[i][0] = \max(dp[i-1][0], dp[i-1][1]) \qquad i \ge 1$
  $dp[i][1] = dp[i-1][0]+money[i] \qquad i \ge 1$

  • $dp[i][0]$은 $i$번째 집을 털지 않고 훔칠 수 있는 돈의 최댓값이기 때문에, 이전 집을 털었든, 털지 않았든 상관없이 그 둘 중 큰 값이 훔칠 수 있는 돈의 최댓값이다.

  • $dp[i][1]$은 $i$번째 집을 털고 훔칠 수 있는 돈의 최댓값이기 떄문에, 이전 집을 털지 않았을 때의 값만을 이용할 수 있다.

    

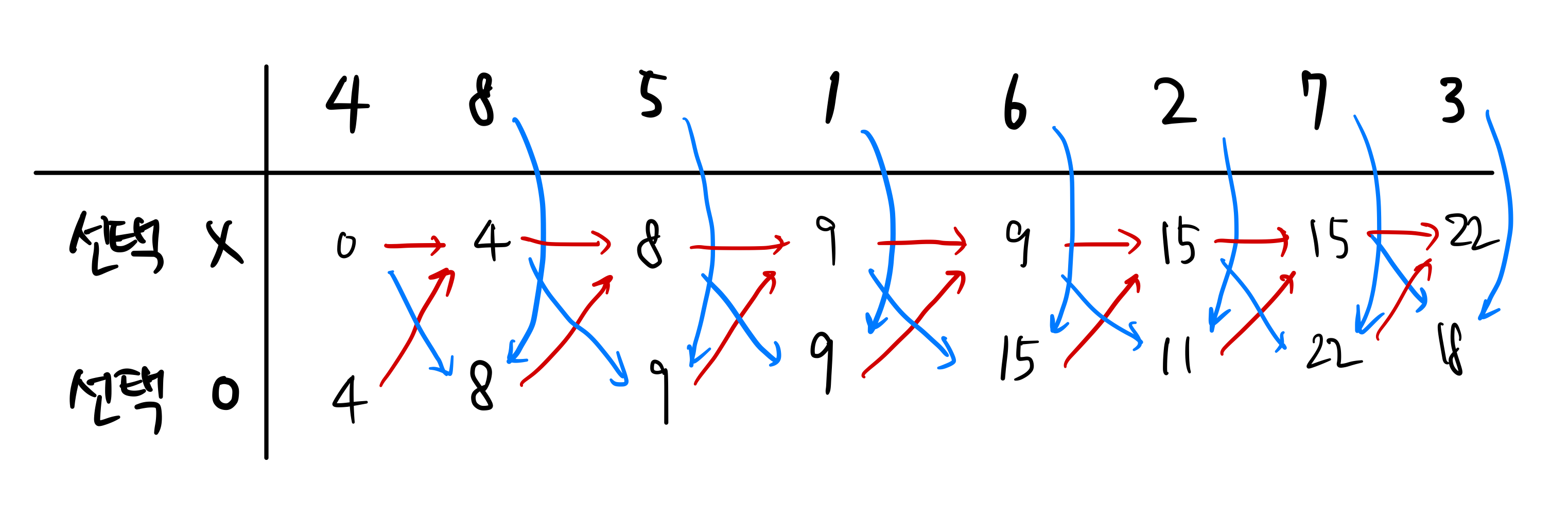
  • (위 점화식대로면 세로로 긴 형태의 테이블이지만 왼쪽에서 오른쪽으로 전이되는 게 눈으로 보기엔 더 직관적이라고 생각해서 transpose된 형태로 그렸다. cache hit rate 면에서도 위 그림과 같은 전이보다 $dp[i][0]$, $dp[i][1]$을 이용하여 전이하는 것이 더 유리하다.)

• 위 점화식을 이용하여 계속하여 전이시켜 나간 다음 $\max(dp[-1][0], dp[-1][1])$이 훔칠 수 있는 돈의 최댓값이다.

첫 번째 집, 마지막 집 인접

• 가장 먼저 생각한 방법(잘못된 생각)은 마지막 집을 털고 훔칠 수 있는 돈의 최댓값($dp[-1][1])$은 첫 번째 집을 털면 안되므로, 여기에서 첫 번째 집에 있는 돈을 빼주는 방법이었다. ($\max(dp[-1][0], dp[-1][1]-money[0])$

  • 하지만 이미 $money[0]$이 포함된 채로 $dp$의 값들이 계산되었으므로 이렇게 처리해주면 안 된다.

• $money[0]$이 포함된 채로 $dp$의 값들이 계산되었다는 점이 문제였다. 그래서 다음과 같이 두 가지 경우로 나누어 생각해볼 수 있었다.

  1. 마지막 집을 고려하지 않고 훔칠 수 있는 돈의 최댓값 (마지막 집을 배제)
  2. 첫 번째 집을 고려하지 않고 훔칠 수 있는 돈의 최댓값 (첫 번째 집을 배제)
  • 두 값 중 최댓값

Solution 1. $O(2n)$

def solution(money):
    
    a, b = 0, money[0]
    for i in range(1, len(money)-1):
        a, b = max(a, b), a+money[i]
    
    c = max(a, b)
    
    x, y = 0, money[1]
    for i in range(2, len(money)):
        x, y = max(x, y), x+money[i]
    
    z = max(x, y)
    
    return max(c, z)

• 더 깔끔하게 for문 한 번으로도 풀어볼 수 있을 것 같은데, 점심 먹고 생각해 보아야 겠다.

---