[백준] 13305 주유소 (C++ - 그리디 알고리즘)

💡 주유소 info

• 문제 제목 : 주유소
• 문제 번호 : 13305
• 레벨 : 실버 III

👀 문제 설명

N개의 도시가 있고, 각 도시엔 하나의 주유소만 있을 때, 가장 왼쪽 도시에서 오른쪽 도시로 갈 때 사용하는 최소의 금액을 찾으면 된다.

예시

위와 같이 4개의 도시가 있고, 각 도시의 주유소 가격은 1L당 5원, 2원, 4원, 1원이다.
각 도시 사이의 거리는 2km, 3km, 1km일 때 최소한의 가격은?

• 1번 도시에서 다 주유하고 갈 때 : 5 x ( 2 + 3 + 1 ) = 30원
• 1번 도시에서 2만큼, 2번 도시에서 3만큼, 3번 도시에서 1만큼 주유할 때
  : 5 x 2 + 2 x 3 + 4 x 1 = 20원
• 그리디 알고리즘 적용 : 1번 도시에서 2만큼, 2번 도시에서 모두 주유하고 갈 때
  : 5 x 2 + 2 x ( 3 + 1 ) = 18원

입력 : 도시의 개수를 나타내는 정수 N(2 ≤ N ≤ 100,000), 인접한 두 도시를 연결하는 도로의 길이(모든 합은 1 ≤ N ≤ 1,000,000,000), 각 주유소의 리터당 가격(1 ≤ N ≤ 1,000,000,000)
출력 : 제일 왼쪽 도시에서 제일 오른쪽 도시로 가는 최소 비용

🚨 주의 사항

• 거리와 비용의 자료형은 long long으로 정의해야한다! (1 ≤ N ≤ 1,000,000,000)
  -> 문제를 제대로 못 보고 int로 했다가 48점을 맞았다 ................ :(
• 첫 번째 도시에선 무조건 주유해햐 한다는 것!
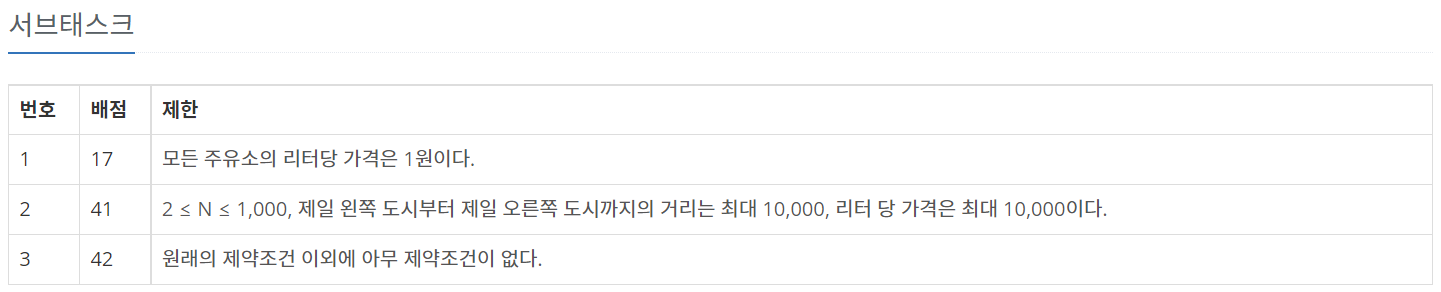
• 서브 태스크를 잘 봐야한다!
  

🔨 해결 방법

너무 쉽게 해결해서 이게 맞나.. 했는데 맞는 것 같다! :)

• if에 해당되지 않아도 total += cost[k] * distance[k]인 것을 볼 수 있다!
  때문에 해당 코드로 첫 번째 주유소에서 무조건 주유할 것!이라는 조건을 만족시킬 수 있다.
• 현재 주유소의 기름값과 다음 주유소의 기름값을 비교했을 때, 현재 주유소의 기름값이 더 크다면 다음 주유소로 가는 거리만큼만 주유하면 된다!
• 다음 주유소의 기름값이 더 크다면 다음 주유소의 기름값을 현재 주유소의 기름값으로 설정하여, 현재 주유소에서 해당 거리만큼 주유하는 것처럼 사용할 수 있다.

#include <iostream>
#include <algorithm>
using namespace std;
#define endl "\n"

int main(){
    cin.tie(0); cout.tie(0);
    int N; // 도시의 개수
    cin >> N;
    
    long long* distance = new long long[N - 1]; // 도시 간의 거리
    for (int i = 0; i < N - 1; i++) {
        cin >> distance[i];
    }

    long long* cost = new long long[N]; // 1리터당 가격
    for (int j = 0; j < N; j++) {
        cin >> cost[j];
    }

    long long total = 0;
    for (int k = 0; k < N-1; k++) {
        if (cost[k] < cost[k+1]) {
            cost[k+1] = cost[k];
        }
        total += cost[k] * distance[k];
    }
    cout << total;
    return 0;
}