[Python3] Knapsack Problem(Dynamic Programming)

진짜 지옥이다,,, 나는 왜케 이게 이해가 안될까....ㅠㅠ
계속 서칭 하다가 도움이 많이된 글이 있어 첨부합니다.ㅠㅠ

평범한 배낭

이 문제는 아주 평범한 배낭에 관한 문제이다.

한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다닐 배낭 또한 최대한 가치 있게 싸려고 한다.

준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다. 아직 행군을 해본 적이 없는 준서는 최대 K만큼의 무게만을 넣을 수 있는 배낭만 들고 다닐 수 있다. 준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값을 알려주자.

입력

첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)가 주어진다.

입력으로 주어지는 모든 수는 정수이다.

출력

한 줄에 배낭에 넣을 수 있는 물건들의 가치합의 최댓값을 출력한다.

예제 입력 1

4 7
6 13
4 8
3 6
5 12

예제 출력 1

14

배낭 문제(Knapsack problem)

배낭 문제: 조합 최적화 문제의 일종이다.
간략하게 말하자면, 담을 수 있는 최대 무게가 정해진 배낭과 함께 각각의 무게와 가치가 주어진 아이템의 집합이 주어졌을 때,배낭에 담은 아이템들의 가치의 합이 최대가 되도록 하는 아이템들의 부분집합을 찾는 문제이다.

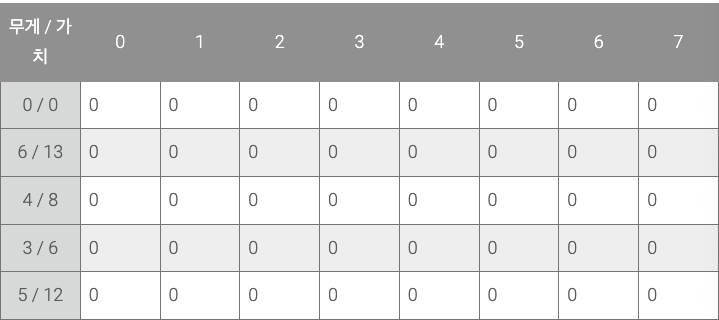
진한 회색으로 나타난 윗쪽의 열 이름(0~7)은 확인할 무게를 뜻한다.
문제에서 주어진 예제에서 준서가 버틸 수 있는 무게를 7로 줬기 때문에 7까지 나타낸 것이다.

연한 회색으로 나타난 왼쪽의 행 이름은 (무게 / 가치) 를 의미한다.

중요

표의 내용은 예를 들어 표의 2행(4 / 8) 3열의 값이 의미하는 것은 그 이전에 등장한 행들(6 / 13)의 경우를 포함해 3kg까지 담을 수 있을 때 얼만큼의 가치를 담을 수 있는지를 저장한다.

즉, 점점 누적이 되어 마지막 행에서는 모든 물품을 담을 수 있는 경우(모든 물품을 담는 다는 것은 아니다)를 구할 수 있고, 마지막 열이 되면 최대 담을 수 있는 7kg까지 모든 물품을 담아서 얻을 수 있는 최대 가치를 구할 수 있다.

첫 번째 물품(6/13)

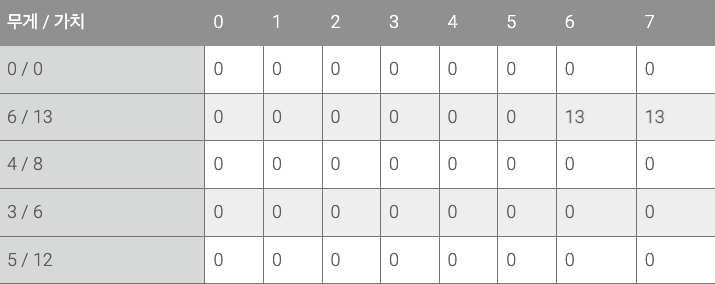
첫 번째 물품은 6kg에 가치가 13이다. 0~5kg 까지는 이 물품을 담을 수 없기 때문에 갱신되지 않고 6kg일 때와 7kg일떄 이 물품을 담아서 13의 가치가 된다.

두 번째 물품(4/8)

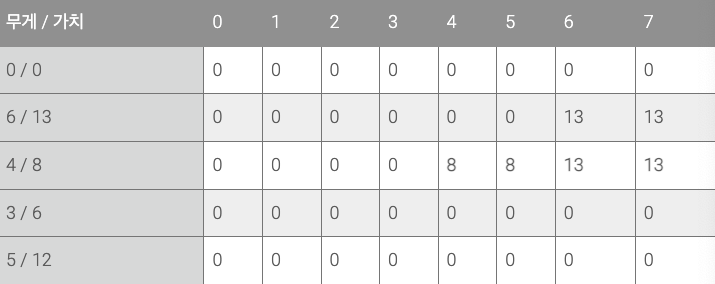
중요!!!!

두 번째 물품은 4kg에 가치가 8이다. 0~3kg 까지는 이 물품을 담을 수 없고, 4~7kg일때 담을 수 있다. 그런데 6kg와 7kg에서는 두 번째 물품을 담는것 보다 첫번째 물품을 담는 것이 더 가치가 높다. 물론 두개 다 담으면 좋겠지만, 7kg를 초과하기 대문에 둘 중 하나만 담을 수 있다.!

세 번째 물품(3/6)

중요!!!!

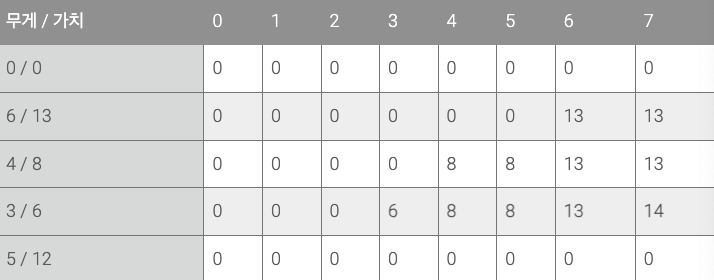
세 번째 물품은 3kg에 가치가 6이다.
Key 1.
3kg일 때 이 물품을 담을 수 있고, 4~6kg 일 때는 이 물품의 가치보다 이전에 4~6kg에 담을 수 있던 물품의 가치가 더 높기 때문에 이전의 값을 저장한다.

Key 2.
7kg에서는 드디어 2개를 동시에 담을 수 있는 상황이 발생한다. 현재 이전(4/8) 물품을 담을 수 있는 경우다. 이때 두 물품의 가치 6 + 8 을해서 14만큼의 가치를 담을 수 있게 된다.

네 번째 물품(5/12)

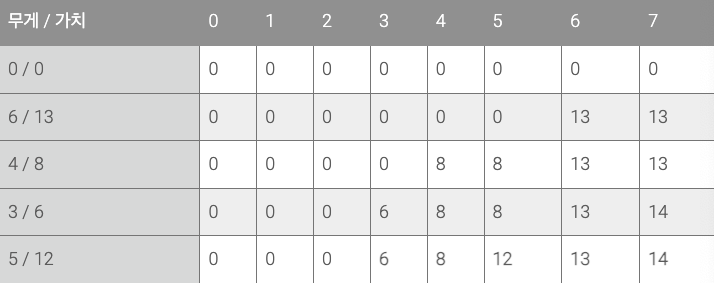
마지막 네 번째 물품은 5kg에 가치가 12이다. 2kg까지는 이전의 어떤 물품도 담을 수 없지만 3kg에서는 세 번쨰 물품을 담을 수 있다. 4kg에서도 마찬가지로 이전의 최대 가치를 가져온다.

5kg에서는 이전에 담을 수 있었던 가치보다 현재 물품을 담는 가치가 더 높기 때문에 현재 물품을 담는다.

6,7kg에서는 현재 물품 5kg와 같이 담을 수 있는 1,2kg 짜리 물품이 없기 때문에 현재 물품만 담거나 이전의 물품을 담아야하는데 이전의 물품의 가치가 13(무게 6짜리 가치),14(3kg + 4kg의 가치)로 더 높기 대문에 이전의 물품들의 가치를 가져온다.

결과적으로 표의 마지막에 담긴 14가 물건들의 가치합의 최대값이 된다.

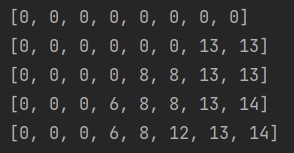
코드로 풀기

표를 채우기 위해 각 물품을 순회하고, 1~ 최대무게(7kg)를 순회해야 한다.

위에서 설명한 상황을 일반화 하자면

1. 현재 확인 중인 무게(y축)보다 현재 확인 중인 물품의 무게(x축)가 더 가볍다면 다른 물품을 추가로 담을 수 있는 상황이다.

   • 이때는 현재 가치 + 이전에 구한의 가치
     (확인 중인 무게 - 현재 무게 == (y축의 무게 - x축의 무게)의 가치
     와 지금까지 구한 현재 확인 중인 무게의 가치의 최댓값
     (y축 -1 의 값 == 이 전까지 파악한 확인중인 무게의 최대값) 중 큰 값을 선택한다.
   • 예를 들어 현재 물품이 (3/6)이고, 현재 확인 중인 무게가 7kg일때 [3kg의 현재 가치(6) + 이전에 구한 4kg에 담을 수 있는 최대 가치 (8)] 와 이전에 구한 7kg에 담을 수 있는 최대 가치(13) 중 큰 값을 구해야한다.

2. 현재 확인 중인 무게보다 현재 확인 중인 물품의 무게가 더 무거운 경우 현재 물품을 담을 수 없기 때문에 이전에 구한 가치 (x축 -1 의 위치의 가치)를 가져온다.

n, max_weight = map(int, input().split())
things = [(0, 0)]
for _ in range(n):
    weight, value = map(int, input().split())
    if weight > max_weight: continue
    things.append((weight, value))

dp = [[0] * (max_weight + 1) for _ in range(len(things))]

for i in range(1, len(things)):  # things[i][0] : 무게, things[i][1] : 가치
    for j in range(1, max_weight + 1):  # j : 현재 확인하는 무게
        dp[i][j] = max(things[i][1] + dp[i - 1][j - things[i][0]], dp[i - 1][j]) if j - things[i][0] >= 0 else dp[i - 1][j]

print(dp[-1][-1])

참조