BOJ #5 : [G4 | 21923] 곡예비행 (python)

문제

동헌이는 모형 비행기 조종 대회에 참가하였다. 이 대회에서는 격자 모양의 공간에서 모형 비행기를 조종하여 얻는 비행 점수로 순위를 매긴다. 격자의 각 칸에는 점수가 부여되어 있고, 비행 점수는 "상승 비행을 할 때 지나간 칸에 부여된 점수의 총합"과 "하강 비행을 할 때 지나간 칸에 부여된 점수의 총합"을 더한 값이다. 출발한 칸과 도착한 칸도 지나간 칸으로 간주한다.

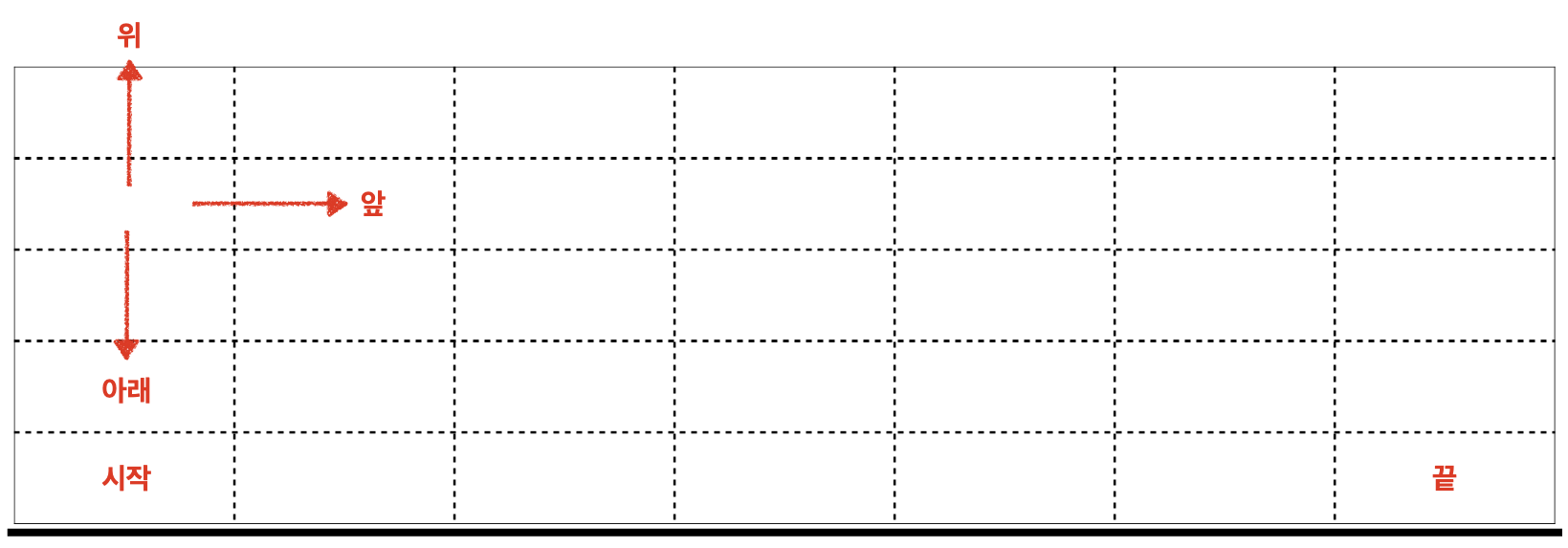
<그림 1> 시작과 끝 칸 및 가능한 이동 방향

모형 비행기는 맨 왼쪽 아래 칸에서 상승 비행으로 비행을 시작해야 하고, 중간에 상승 비행에서 하강 비행으로 변경한 후, 맨 오른쪽 아래 칸에서 하강 비행으로 비행을 종료해야 한다. 상승 비행에서 하강 비행으로 변경할 때에는 다른 칸으로 이동할 수 없다. 즉, 상승 비행이 끝난 칸에서 하강 비행을 시작해야 한다.

모형 비행기는 상승 비행 중에는 앞 또는 위로만 이동할 수 있고, 하강 비행 중에는 앞 또는 아래로만 이동할 수 있다.

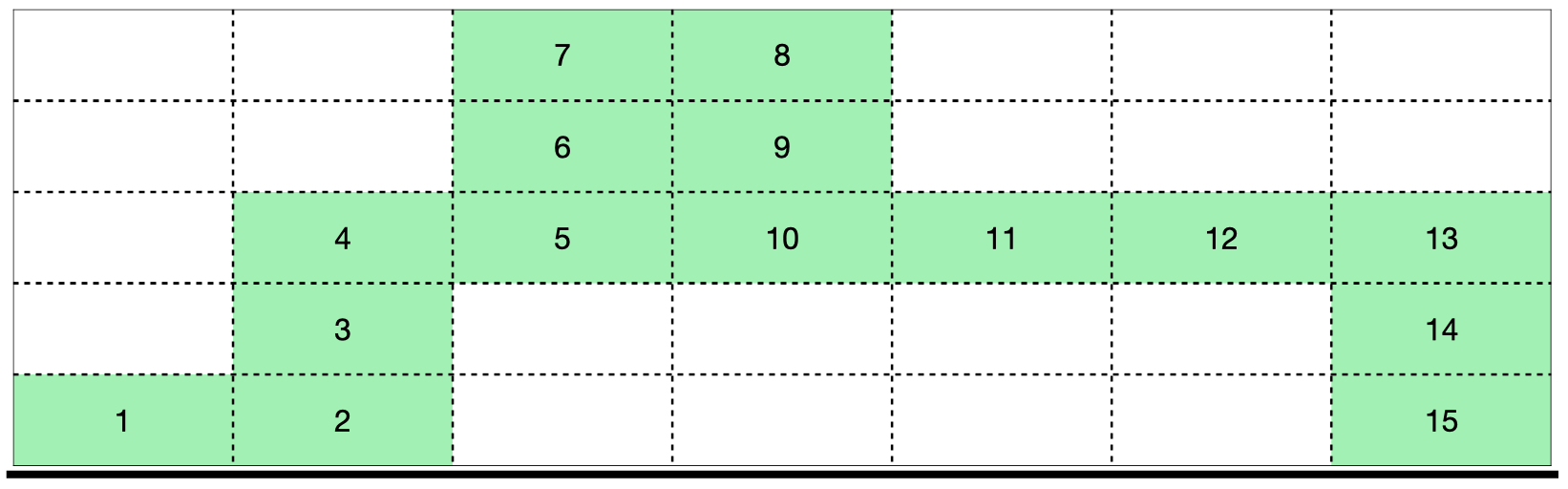
<그림 2> 모형 비행기의 이동 경로

위의 예시에서, 각 칸에 적힌 수는 그 칸에 부여된 점수이고, 수가 적혀 있지 않은 칸의 점수는 0이라고 가정하자. 그리고 모형 비행기가 1, 2, ..., 15의 순서대로 비행을 했다고 가정하자.

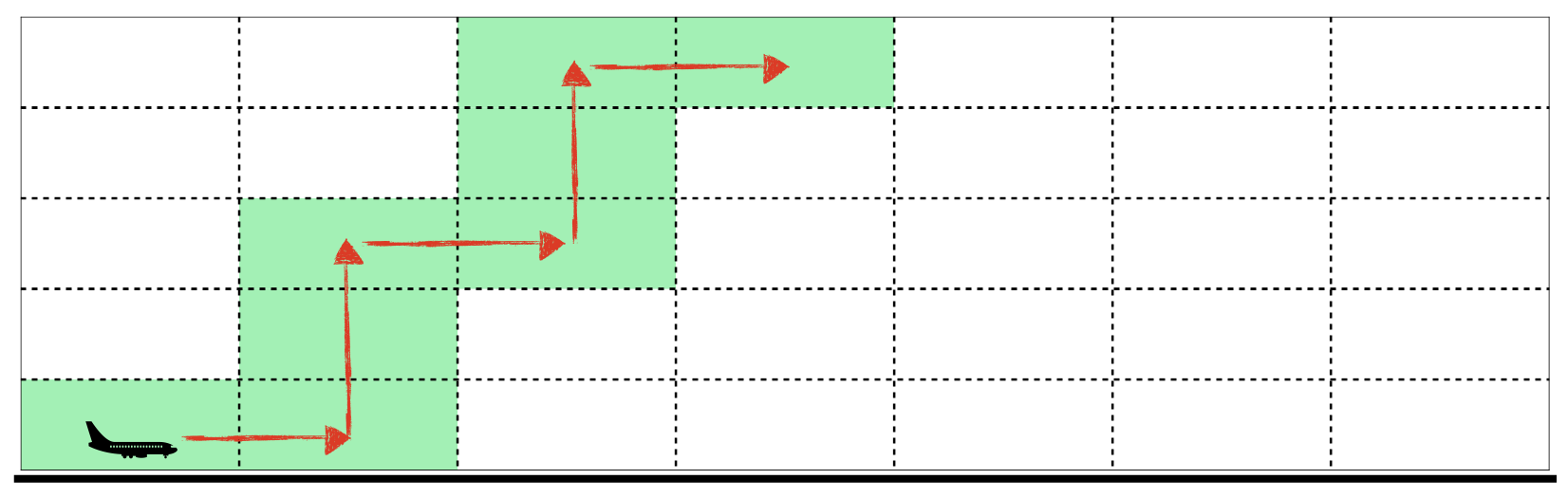
<그림 3> 상승 비행의 이동 경로

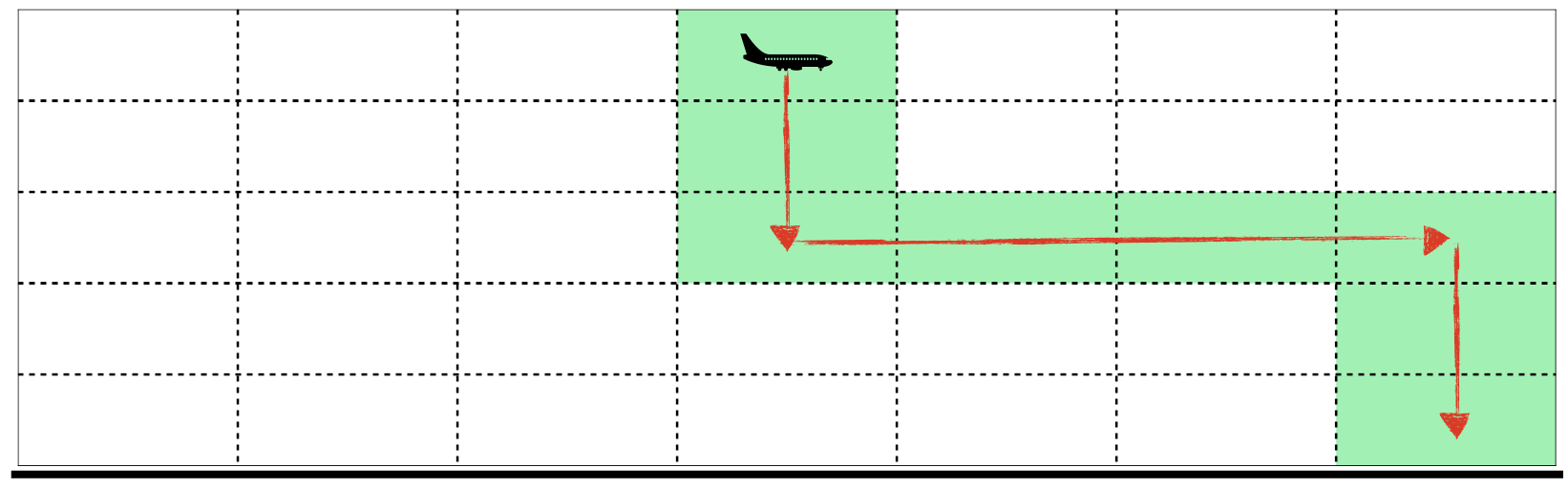
<그림 4> 하강 비행의 이동 경로

이 경우, 상승 비행은 1이 적힌 칸에서 시작하고 8이 적힌 칸에서 끝난다. 하강 비행은 8이 적힌 칸에서 시작하고 15가 적힌 칸에서 끝난다. 이와 같이 비행을 하였을 때 얻는 점수는 (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8) + (8 + 9 + 10 + 11 + 12 + 13 + 14 + 15) = 128 이다.

동헌이는 이 대회에서 얻을 수 있는 최대 비행 점수가 궁금하다. 동헌이를 위해 얻을 수 있는 최대 비행 점수를 구해주자.

입력

첫째 줄에 심사위원들이 나눠놓은 구역(격자)의 세로 길이
$N$, 가로 길이
$M$이 공백과 함께 주어진다.

두 번째 줄부터
$N+1$번째 줄까지, 각 칸에 해당하는 점수가 한 줄에 한 행씩 공백과 함께 주어진다.

출력

동헌이가 얻을 수 있는 최대 점수를 출력하라.

문제 설명

• 비행기는 기본적으로 두가지 상태(상승, 하강)가 존재한다.
• 상승 경로와 하강 경로의 점수의 합의 최대값을 출력한다.
• 상승의 마지막 경로와 하강의 처음 경로는 중복된다.

사고 과정

각 구역까지의 최대 점수를 DP를 이용해 저장하면 될 것으로 보인다.
dp는 상승구간(0) 과 하강구간(1)로 두가지로 저장한다.

이때 상승구간을 먼저 계산한 후에 하강구간을 저장한다.

• 상승구간 점수는 현재의 점수에 다음 경우들중 최대값을 더한 값이다
  • 현재 칸에서 왼쪽 점수 (왼쪽에서 이동한 경우) : dp[i][j-1][0]
  • 현재 칸에서 아래쪽의 점수 (아래에서 위로 올라간 경우) : dp[i+1][j][0]
• 하강구간 점수는 현재의 점수의 다음 경우들중 최대값을 더한 값이다.
  • 현재 칸의 상승구간 점수 (상승-> 하강 변화) : dp[i][j][0]
  • 현재 칸에서 위의 점수 (위에서 아래로 내려간 경우) : dp[i-1][j][1]
  • 현재 칸에서 왼쪽의 점수 (왼쪽에서 이동한 경우) : dp[i][j-1][1]

코드

import sys

input = sys.stdin.readline


def solve():
    N, M = map(int, input().split())
    score_table = [list(map(int, input().split())) for _ in range(N)]

    # DP 테이블, 0 : 상승 1 : 하강
    DP = [[[None for _ in range(2)] for _ in range(M)] for _ in range(N)]

    # 상승 구간 계산
    DP[N - 1][0][0] = score_table[N-1][0]
    # 가장 왼쪽 열을 계산
    for i in range(N - 2, -1, -1):
        DP[i][0][0] = score_table[i][0] + DP[i + 1][0][0]
    # 가장 아래 행을 계산
    for j in range(1, M):
        DP[N-1][j][0] = DP[N-1][j - 1][0] + score_table[N-1][j]
    # 나머지 구역 계산
    for i in range(N - 2, -1, -1):
        for j in range(1, M):
            DP[i][j][0] = max(DP[i][j - 1][0], DP[i + 1][j][0]) + score_table[i][j]

    # 하강 구간 계산
    DP[0][0][1] = DP[0][0][0] + score_table[0][0]
    # 가장 윗 행 계산
    for j in range(1, M):
        DP[0][j][1] = max(DP[0][j][0], DP[0][j - 1][1]) + score_table[0][j]
    # 가장 왼쪽 행 계산
    for i in range(1, N):
        DP[i][0][1] = max(DP[i][0][0], DP[i-1][0][1]) + score_table[i][0]
    # 나머지 구역 계산
    for i in range(1, N):
        for j in range(1,M):
            DP[i][j][1] = max(DP[i][j][0], DP[i - 1][j][1], DP[i][j-1][1]) + score_table[i][j]

    print(DP[N-1][M-1][1])
solve()