[Algorithm] BackTracking 백트래킹, 백준 9663 N-Queen 문제

Madeline👩🏻‍💻·2023년 6월 14일

Backtracking 백준 백트래킹 알고리즘

코테준비

목록 보기

3/7

😈 백트래킹

1. 백트래킹이 뭐야

제약조건 만족문제에서 사용하는 방법이다.

DFS vs Backtracking

DFS는 가능한 모든 경로(후보군)을 탐색한다. 불필요한 후보군을 제외하지 않아서, 경우의 수를 최적으로 줄이지 못한다.
-> N! 의 경우의 수를 가지는 문제는 DFS로 처리하지 못한다.

백트래킹은 해를 찾는 과정에서, 불필요한 루보군은 제외한다. 따라서 DFS보다 효율적이다. 하지만, N!의 경우의 수를 가지는 문제에서 시간복잡도 때문에 처리 불가능할 수 있다. 그래서 가지치기를 잘해야 한다.

=> Backtracking = DFS + 조건문 인듯 하다!

2. Logic

1) 해를 찾기 위해, 트리 구조 기반으로 후보군에 대해 제약 조건을 점진적으로 체크하다가(DFS),
-> 각 후보군은 DFS 방식으로 체크(Promising)
2) 해당 후보군이 제약 조건을 만족하지 않으면, backtrack(퇴각)!
3) 다시는 그 후보군을 체크하지 않게 표시(가치지기 - Pruning)
4) 다른 후보군으로 넘어가면서, 최적의 해를 찾는 방법

Promising: 해당 루트가 조건에 맞는지를 검사하는 기법
Pruning (가지치기): 조건에 맞지 않으면 포기하고 다른 루트로 바로 돌아서서, 탐색의 시간을 절약하는 기법

N-Queen 문제

https://www.acmicpc.net/problem/9663

문제
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다.

N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.

입력
첫째 줄에 N이 주어진다. (1 ≤ N < 15)

출력
첫째 줄에 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 출력한다.

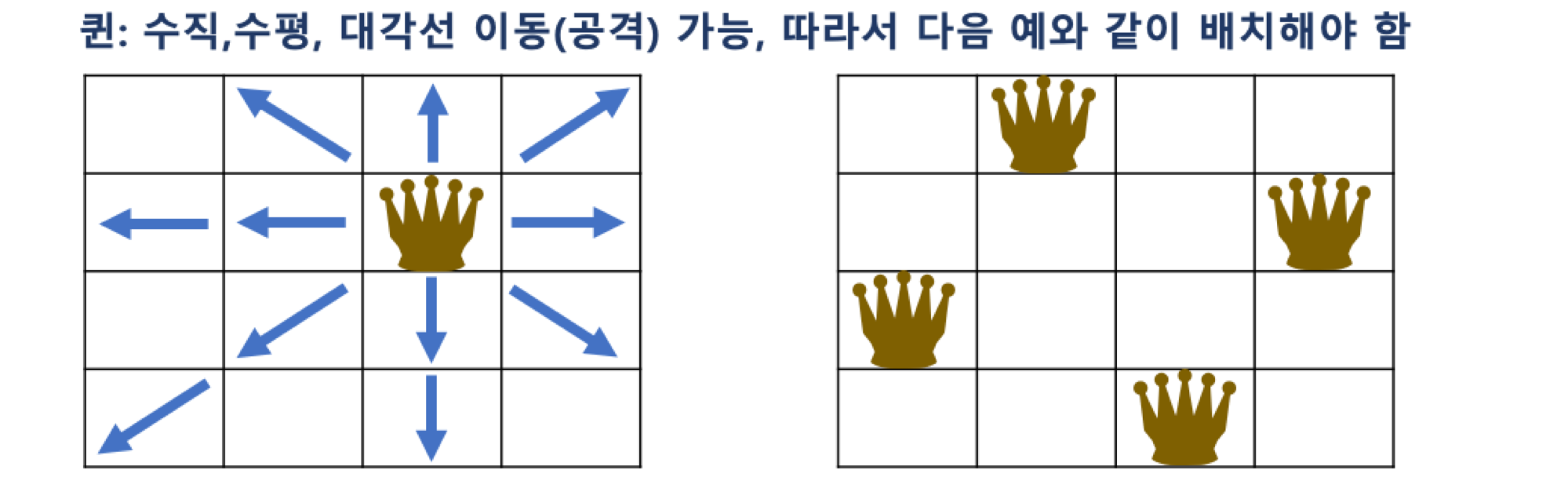
대표적인 백트래킹 문제
NxN 크기의 체스판에 N개의 퀸을 서로 공격할 수 없도록 배치하는 문제
🤐 조건 : 퀸이 놓였을 때 퀸 자신을 기준으로 일직선상(가로 및 세로)과 대각선 방향에는 아무것도 놓여있으면 안 된다. 배치된 퀸이 공격할 수 없는 위치로 배치해야 함

Logic

1) Promising 인지 체크하는 함수
퀸이 서로 공격을 하지 못할려면, 같은 가로, 세로, 대각선 상에 있으면 안 된다.

다른 행, 열에 있는지
대각선에 없는지

2) 크기가 N인 일차원 배열을 만든 후, 각 행의 몇 번째 열에 퀸이 있는지를 저장하는 방식
예를 들어 N = 4일때, 일차원 배열 row [] 에 아래와 같이 저장하면 된다.
row[0] = 2
0행 2열에 퀸 존재
row[1] = 0
1행 0열에 퀸 존재

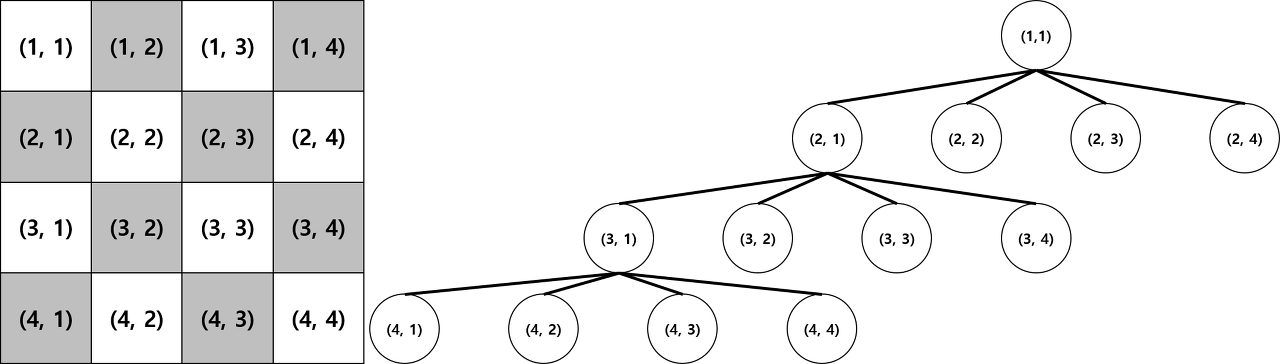
(1,1) 을 시작 지점으로 보고 DFS 를 진행

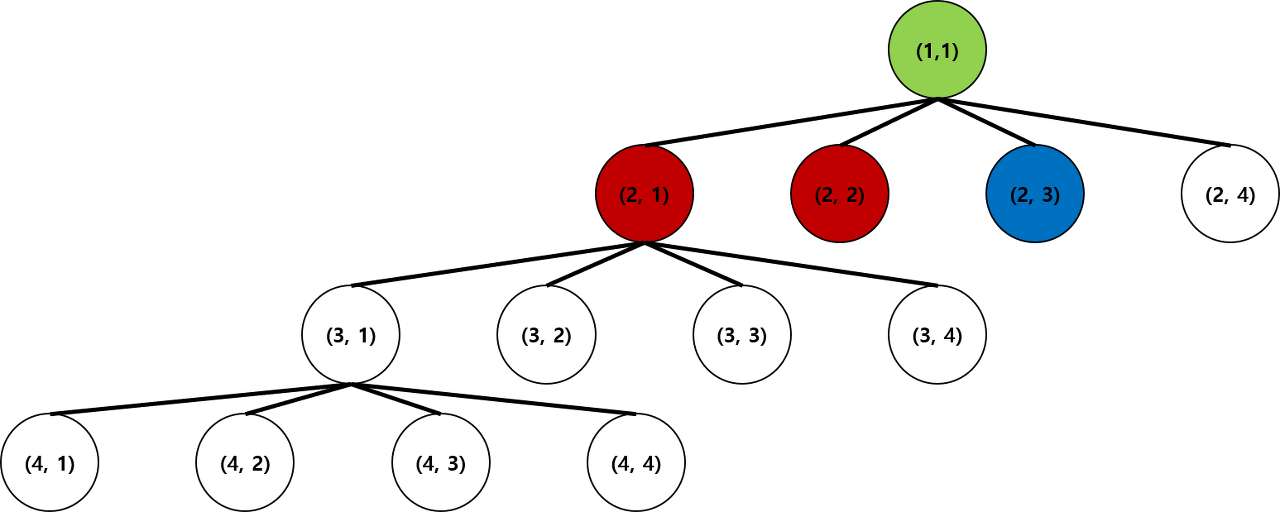
-> (2,1) : (1,1)에 있는 퀸이 공격할 수 있음 -> Pruning
-> (2,2) : 퀸이 공격할 수 있음 -> Pruning
-> (2,3) : 조건에 부합(퀸이 공격 못함) -> DFS 진행

//
//  9663.cpp
//  Backtracking
//  BOJ 9663 N-Queen 문제
//

#include <iostream>
#include <vector>

using namespace std;

int N;//크기가 NxN인 체스판
int answer = 0;//퀸을 놓는 경우의 수
int loc[15];// (1 ≤ N < 15)

bool isPromising(int row){//조건을 만족하는지
    for(int i=0;i<row;i++){
        //같은 행,열인지 or 대각선인지 검사
        if((loc[i] == loc[row]) || (row-i)==(abs(loc[row]-loc[i]))){
            return 0;
        }
    }
    return 1;
}

void NQueen(int row){
    if(row == N){//N번째 행까지 다 돌았음
        answer += 1;
        return;
    }
    else{
        for(int i=0;i<N;i++){
            loc[row] = i;// row[0] = 2 -> 0행 2열에 퀸 존재
            
            if (isPromising(row)){
                NQueen(row+1);// 다음 행
            }
        }
    }
}

int main() {
    cin>> N;
    NQueen(0);//0번째 행부터 시작
    cout<< answer;
    
    return 0;
}