잊지말자 알고리즘,,

위상 정렬이 뭐야

순서가 정해져있는 작업을 차례로 수행해야할 때, 그 순서를 결정해주기 위해 사용하는 알고리즘!

-> 그래프의 흐름 = 조건

• 위상정렬은 여러개의 답이 존재할 수 있다는 점에서 매력적임 😎

• DAG(Directed Acyclic Graph)에만 적용 가능 -> cycle이 있다면 위상정렬 적용 x
  - 왜냐면 위상정렬은 시작점이 있어야함

• 그래서 위상정렬을 쓰면 알 수 있는게 1) 위상 정렬이 가능한 그래프인지? 2) 가능하면 그 결과가 뭔지?

위상 정렬을 수행하는 알고리즘

1. 스택
2. 큐

큐를 이용해서 위상정렬

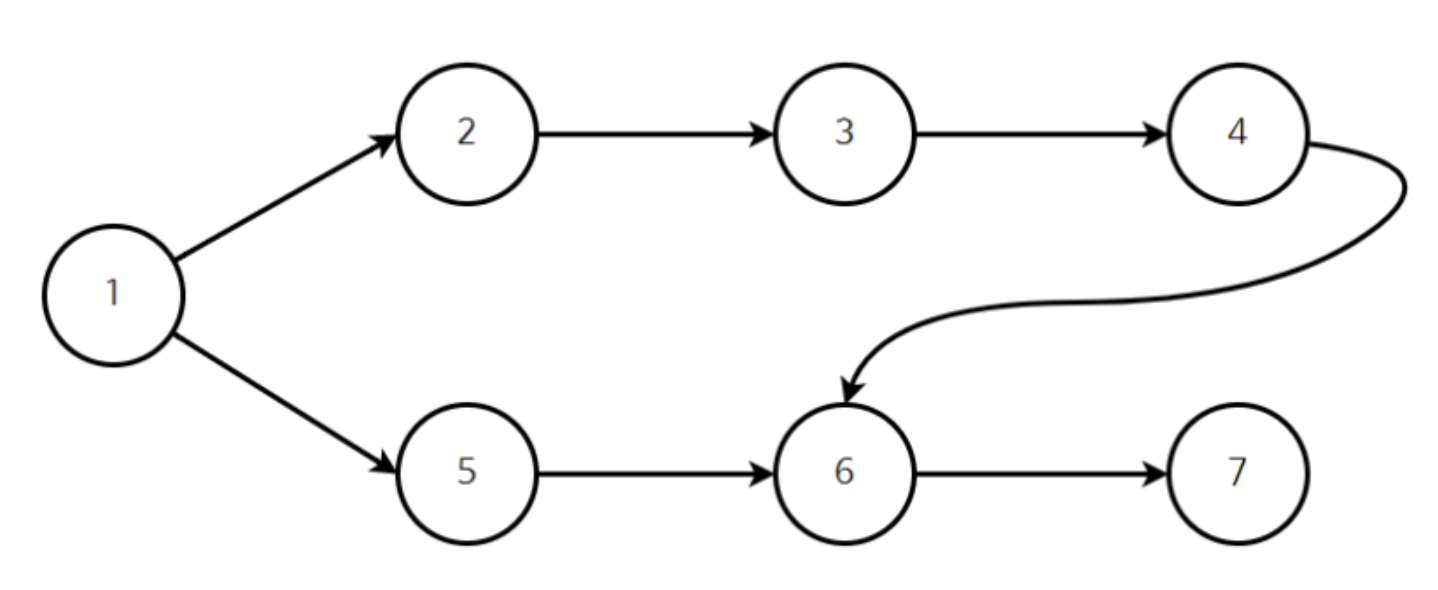
1) 진입차수가 0인 정점을 큐에 삽입 (==시작점)
2) 큐에서 원소를 꺼내 연결된 모든 간선을 제거
3) 진입차수가 0이 된 정점을 큐에 삽입
4) 2~3번 반복 - 큐가 빌 때까지!
- 만약에 모든 원소를 돌기 전에 큐가 비어? 그러면 사이클이 존재하는 것임
- 모든 원소를 다 돌았어? 그러면 큐에서 꺼낸 순서가 위상 정렬의 결과

//
//  main.cpp
//  topologyTrial
//
//  Created by 신정연 on 2023/07/26.
//

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

int n;
int inDegree[10];//진입차수
vector<int> a[10];//진입차수와 연결된 노드 담아

void topologySort(){
    int result[10];
    queue<int> q;
    //진입 차수가 0인 노드 -> 큐
    for(int i=1;i<=n;i++){
        if(inDegree[i]==0){
            q.push(i);
        }
    }
    //n개의 노드를 방문 == 위상정렬임
    for(int i=1;i<=n;i++){
        //그 전에 큐가 비어? == 사이클임
        if(q.empty()){
            cout << "cycle";
            return;
        }
        int x = q.front();
        q.pop();//원소 제거
        result[i] = x;//그걸 result에 담아 -> 결과적으로 위상정렬 순서
        //연결된 모든 간선을 제거 == 진입차수를 1빼줌
        for(int i=0;i<a[x].size();i++){
            int y = a[x][i];
            inDegree[y]--;
            //진입차수가 0인거 큐에 삽입
            if(inDegree[y]==0){
                q.push(y);
            }
//            if(--inDegree[y] == 0){
//                q.push(y);
//            }
        }
    }
    for(int i=1;i<=n;i++){
        cout << result[i];
    }
}

int main(){
    n=7;
    a[1].push_back(2);
    inDegree[2]++;
    a[1].push_back(5);
    inDegree[5]++;
    a[2].push_back(3);
    inDegree[3]++;
    a[3].push_back(4);
    inDegree[4]++;
    a[4].push_back(6);
    inDegree[6]++;
    a[5].push_back(6);
    inDegree[6]++;
    a[6].push_back(7);
    inDegree[7]++;
    topologySort();
}

출력: 1253467

시간복잡도

위상정렬의 시간복잡도는 O(V+E)
정점의 개수 + 간선의 개수만큼 소요되므로 아주 빠름~

레퍼런쓰
https://m.blog.naver.com/ndb796/221236874984