예제: 드래곤 커브
문제
재현시의 시장 구재현은 지난 몇 년간 게리맨더링을 통해서 자신의 당에게 유리하게 선거구를 획정했다. 견제할 권력이 없어진 구재현은 권력을 매우 부당하게 행사했고, 심지어는 시의 이름도 재현시로 변경했다. 이번 선거에서는 최대한 공평하게 선거구를 획정하려고 한다.재현시는 크기가 N×N인 격자로 나타낼 수 있다. 격자의 각 칸은 구역을 의미하고, r행 c열에 있는 구역은 (r, c)로 나타낼 수 있다. 구역을 다섯 개의 선거구로 나눠야 하고, 각 구역은 다섯 선거구 중 하나에 포함되어야 한다. 선거구는 구역을 적어도 하나 포함해야 하고, 한 선거구에 포함되어 있는 구역은 모두 연결되어 있어야 한다. 구역 A에서 인접한 구역을 통해서 구역 B로 갈 수 있을 때, 두 구역은 연결되어 있다고 한다. 중간에 통하는 인접한 구역은 0개 이상이어야 하고, 모두 같은 선거구에 포함된 구역이어야 한다.
선거구를 나누는 방법은 다음과 같다.
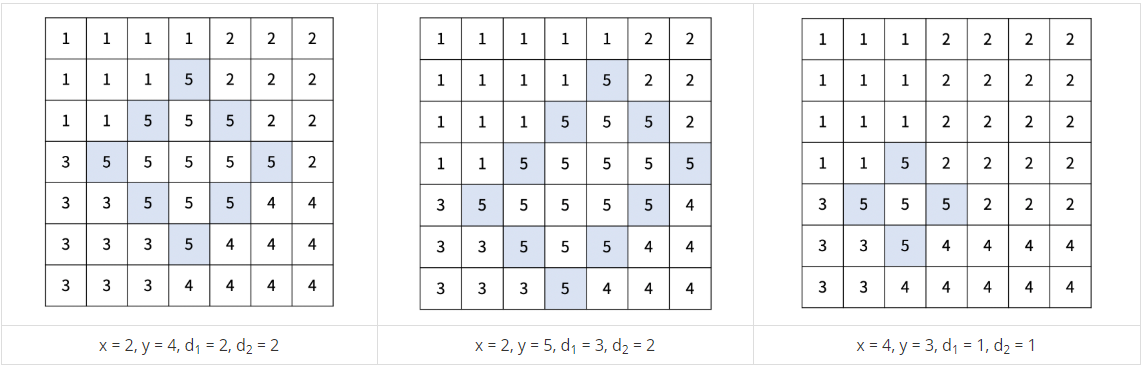
- 기준점 (x, y)와 경계의 길이 d1, d2를 정한다. (d1, d2 ≥ 1, 1 ≤ x < x+d1+d2 ≤ N, 1 ≤ y-d1 < y < y+d2 ≤ N)
- 다음 칸은 경계선이다.
1) (x, y), (x+1, y-1), ..., (x+d1, y-d1)
2) (x, y), (x+1, y+1), ..., (x+d2, y+d2)
3) (x+d1, y-d1), (x+d1+1, y-d1+1), ... (x+d1+d2, y-d1+d2)
4) (x+d2, y+d2), (x+d2+1, y+d2-1), ..., (x+d2+d1, y+d2-d1)- 경계선과 경계선의 안에 포함되어있는 5번 선거구이다.
- 5번 선거구에 포함되지 않은 구역 (r, c)의 선거구 번호는 다음 기준을 따른다.
1) 1번 선거구: 1 ≤ r < x+d1, 1 ≤ c ≤ y
2) 2번 선거구: 1 ≤ r ≤ x+d2, y < c ≤ N
3) 3번 선거구: x+d1 ≤ r ≤ N, 1 ≤ c < y-d1+d2
4) 4번 선거구: x+d2 < r ≤ N, y-d1+d2 ≤ c ≤ N아래는 크기가 7×7인 재현시를 다섯 개의 선거구로 나눈 방법의 예시이다.
구역 (r, c)의 인구는 A[r][c]이고, 선거구의 인구는 선거구에 포함된 구역의 인구를 모두 합한 값이다. 선거구를 나누는 방법 중에서, 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이의 최솟값을 구해보자.
입력
첫째 줄에 재현시의 크기 N이 주어진다.둘째 줄부터 N개의 줄에 N개의 정수가 주어진다. r행 c열의 정수는 A[r][c]를 의미한다.
출력
첫째 줄에 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이의 최솟값을 출력한다.제한
5 ≤ N ≤ 20 1 ≤ A[r][c] ≤ 100예제 입력 1
6 1 2 3 4 1 6 7 8 9 1 4 2 2 3 4 1 1 3 6 6 6 6 9 4 9 1 9 1 9 5 1 1 1 1 9 9예제 출력 1
18예제 입력 2
6 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5예제 출력 2
20예제 입력 3
8 1 2 3 4 5 6 7 8 2 3 4 5 6 7 8 9 3 4 5 6 7 8 9 1 4 5 6 7 8 9 1 2 5 6 7 8 9 1 2 3 6 7 8 9 1 2 3 4 7 8 9 1 2 3 4 5 8 9 1 2 3 4 5 6예제 출력 3
23
풀이
문제 이해는 그렇게 어렵지 않았지만, 일반적인 x, y의 좌표계 방향의 변경, 까다롭게 보이는 수학식 등이 풀이를 크게 방해하는 요소였다.
또한, 문제에 주어져있는 범위조건을 x, y, d1, d2를 선정하는데에 잘 녹아들게 해야하는 점이 어려웠다.
필자는 처음에
1. 조건에 따라 x, y, d1, d2 설정(4중 for문)
2. 5번 구역 marking
3. 1~4번 구역 marking
4. 인구수 총합 차의 최소값 구하기
의 알고리즘으로 풀었는데, 생각보다 속도가 느렸다. 그래서
- 조건에 따라 x, y, d1, d2 설정(4중 for문)
- x, y를 따라가며(2중 for문) 선거구에 해당하는 부분에서 각 선거부 인구수를 합산
- 인구수 총합 차의 최소값 구하기
로 바꿨는데, 생각보다 많이 빨라지지 않더라..
전체적인 소스코드는 아래와 같다.
소스 코드
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int INF = 987654321;
int N;
int map[21][21];
int diff(int x, int y, int d1, int d2) {
vector<int> population(5, 0);
for (int r = 1; r <= N; r++) {
for (int c = 1; c <= N; c++) {
//1번 선거구
if (r < x + d1 && c <= y && !(r >= x && c >= y - (r - x))) {
population[0] += map[r][c];
}
//2번 선거구
else if (r <= x + d2 && c > y && !(r >= x && c <= y + (r - x))) {
population[1] += map[r][c];
}
//3번 선거구
else if (r >= x + d1 && c < y - d1 + d2 && !(r <= x + d1 + d2 && c >= (y - d1 + d2 - (x + d1 + d2 - r)))) {
population[2] += map[r][c];
}
//4번 선거구
else if (r > x + d2 && c >= y - d1 + d2 && !(r <= x + d1 + d2 && c <= (y - d1 + d2 + (x + d1 + d2 - r)))) {
population[3] += map[r][c];
}
//5번 선거구
else {
population[4] += map[r][c];
}
}
}
sort(population.begin(), population.end());
return population[4] - population[0];
}
int minDiff() {
int res = INF;
for (int x = 1; x <= N - 2; x++) {
for (int y = 2; y <= N - 1; y++) {
for (int d1 = 1; d1 <= y - 1 && d1 <= N - x - 1; d1++) {
for (int d2 = 1; d2 <= N - y && d2 <= N - x - 1; d2++) {
res = min(res, diff(x, y, d1, d2));
}
}
}
}
return res;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cin >> N;
for (int x = 1; x <= N; x++) {
for (int y = 1; y <= N; y++) {
cin >> map[x][y];
}
}
cout << minDiff() << endl;
return 0;
}풀이 후기
몇 사람의 풀이 결과를 보니 0ms도 있던데, 필자는 16ms가 최대였다.
인구수 합산하는 로직일수도 있고, 적당히 break 등으로 걸러주는 과정이 더 필요할 것 같다.
근시일 내에 꼭 다시 풀어봐야 할 문제이다.