예제: Lowest Common Ancestor of a Binary Search Tree
문제
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
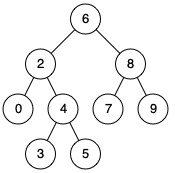
Given binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]
Example 1:
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 Output: 6 Explanation: The LCA of nodes 2 and 8 is 6.Example 2:
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 Output: 2 Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
풀이
이진 탐색 트리에서 두 노드의 주소가 주어질 때, lowest common ancestor (LCA) 라는 것을 찾으라는 문제이다. 즉, 공통이 되는 부모 노드의 주소를 찾으라는 것이다. 유의할 점은, 주어진 두 노드중 하나가 LCA 일 수도 있다는 것이다.
필자는 이를 재귀함수로 풀었는데, 로직은 다음과 같다.
p > q 이라고 할 때(->val 생략),
root node가 LCA인 경우는 아래 3가지이다.
1) p < root < q;
2) p <= root < q;
3) q < root <= q;
위의 3가지 경우 중 하나가 나올 때까지 재귀함수를 호출하면 되겠다.
전체적인 소스코드는 아래와 같다.
소스 코드
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (p->val > q->val)
return solve(root, q, p);
else
return solve(root, p, q);
}
TreeNode* solve(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root->val == p->val && root->val < q->val) {
return root;
}
else if (root->val == q->val && root->val > p->val) {
return root;
}
else if (root->val > p->val && root->val < q->val) {
return root;
}
if (root->val > q->val) {
return lowestCommonAncestor(root->left, p, q);
}
else {
return lowestCommonAncestor(root->right, p, q);
}
}
};풀이 후기
꼭 초심을 되찾고 열심히 하려고 마음을 먹은 다음날에는 핵야근이 기다리고 있다.
시련인가.. 지지않아!😤