다음 큰 숫자

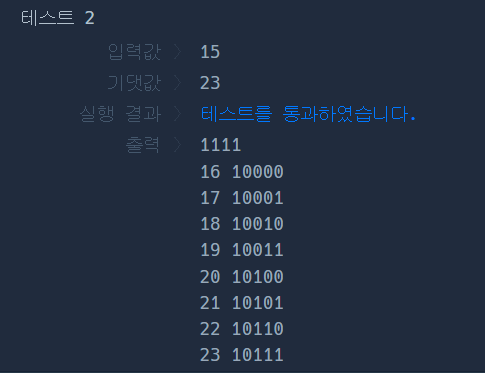
아니나 다를까 너무 정직한 풀이라서 시간이 오래 걸린다.

다른 사람 풀이를 보니 bitCount()라는 메소드가 있다.

Integer.bitCount(int x) : 입력된 32비트 정수의 1의 개수를 계산합니다.
Long.bitCount(long x) : 입력된 64비트 정수의 1의 개수를 계산합니다.
하드웨어 수준에서 최적화된 거라 수행속도도 빠르다고 한다.

1차 풀이

class Solution {
    public int solution(int n) {
        int answer = 0;
        String binaryString = Integer.toBinaryString(n);
        int count = 0, temp;
        int i, j;
        
        System.out.println(binaryString);
        //이렇게 하면 시간이 너무 오래 걸릴거 같은데....
        for(i = 0; i < binaryString.length(); i++){
            if(binaryString.charAt(i) == '1'){
                count++;
            }
        }
        
        while(true){
            n++;
            String tempBinaryString = Integer.toBinaryString(n);
            temp = 0;
            
            System.out.println(n + " " + tempBinaryString);
            for(i = 0; i < tempBinaryString.length(); i++){
                if(tempBinaryString.charAt(i) == '1'){
                    temp++;
                }
            }
            if(temp == count){
                answer = n;
                break;
            }
        }
        
        return answer;
    }
}

2차 풀이

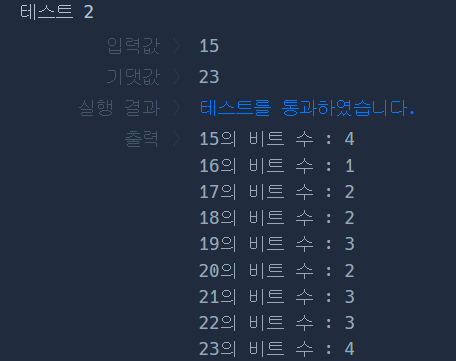
확실히 조금 더 빠르긴 하다.

class Solution {
    public int solution(int n) {
        int answer = 0;
        int count = 0, temp = 0;
        
        count = Integer.bitCount(n);
        System.out.println(n + "의 비트 수 : " + count);
        
        while(temp != count){
            n++;
            temp = Integer.bitCount(n);
            System.out.println(n + "의 비트 수 : " + temp);
        }
        answer = n;
        
        return answer;
    }
}