백준 17087 java : 유클리드 호제법

유클리드 호제법을 사용해 최대공약수 구하기

수빈이의 위치에서 동생들을 찾아야 하는데 동일한 거리만 이동할 수 있고 배수는 상관 없음. -> 동생들 위치에서 수빈이 위치를 뺀 것이 동생과 수빈이의 거리 -> 각 거리의 최대공약수를 구하면 수빈이는 동일한 거리로 배수 상관없이 모든 동생을 찾을 수 있음.

유클리드 호제법

while (b != 0){
   temp = a % b;
   a = b;
   b = temp;
}
return a;

a가 a와 b의 최대공약수이다.

import java.util.Scanner;

public class BJ17087 {
    static Scanner sc = new Scanner(System.in);
    static int N, S;
    static int [] brothers;

    public static void main(String[] args) {
        inputData();
        System.out.println(findAnswer());
    }

    public static void inputData(){
        int i;

        N = sc.nextInt();
        S = sc.nextInt();
        brothers = new int[N];
        for(i = 0; i < N; i++){
            brothers[i] = sc.nextInt();
        }

        sc.close();
    }

    public static int findAnswer(){
        int answer = 0;
        int i, gcd = 0, a, b;

        //동생이 한명인 경우
        if(brothers.length == 1){
            return Math.abs(S - brothers[0]);
        }

        //동생들 위치에서 수빈이 위치 빼기
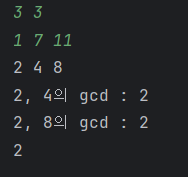
        for(i = 0; i < brothers.length; i++){
            brothers[i] = Math.abs(S - brothers[i]);
            System.out.print(brothers[i] + " ");
        }
        System.out.println();

        //원소들의 최대공약수 구하기
        a = brothers[0];
        for(i = 1; i < brothers.length; i++){
            b = brothers[i];
            gcd = GCD(a, b);
            System.out.println(a + ", " + b + "의 gcd : " + gcd);
            a = gcd;
        }

        return gcd;
    }

    public static int GCD(int a, int b){
        int temp;

        while (b != 0){
            temp = a % b;
            a = b;
            b = temp;
        }

        return a;
    }
}