레드블랙트리-1(개요와 삽입까지)

Mr.뉴트리아·2020년 10월 18일
알고리즘자료구조
2

자료구조 이것저것

목록 보기
2/2

저번에 이진 탐색 알고리즘을 진행하면서, 이진 탐색 트리(BST)의 균형이 무너진 모양과 간단한 예시를 들어봤습니다. 그렇다면 이는 어떻게 처리해야할까요? 사실 이진 탐색 알고리즘 자체만으로는 힘들다고 말할 수 있습니다. BST의 Remove_node함수를 균형을 유지하는쪽으로 작성했지만, 불균형의 근본적인 원인은 BST의 삽입에 있으니까요.
그러면 이를 어떻게 처리해야할까요?

균형의 수호자 닥터 레드블랙트리

혹시 마블영화 좋아하시나요? 마블 세계관은요? 수많은 매력적인 영웅들이 있지만, 저는 그 중에서 닥터 스트레인지를 제일 좋아합니다. 눈이 휘둥그레지는 마법으로 우주의 질서와 균형을 지키는 모습은 정말 멋지죠!(베네딕트 컴버배치 배우를 제일 좋아하는 것도 있습니다 ㅎㅎ)

                              	      우와... 쩐다..

그런데 그거 아시나요? 자료구조에도 닥터 스트레인지같이 균형의 수호자가 있단 것을요?
그것이 바로 "레드블랙 트리"입니다.

물론 닥터 스트레인지보다는 한없이 초라한 모습입니다.

레드 블랙 트리 노드의 구조체는 대략 이런 모습입니다.

enum Color{ RED, BLACK };
struct RBTNode
{
	struct RBTNode* parent;
	struct RBTNode* left;
	struct RBTNode* right;

	int data;
	enum Color color;
	
};

저번 BST노드에는 보이지 않았던 두 친구가 있죠? color와 parent 포인터 말이에요.

enum이라는 타입을 가진 color 변수는 열거형 변수라고 부릅니다. 우리는 저 값을 바탕으로 해당 노드의 색깔을 구분할 수 있습니다.
Parent포인터는 이름 그대로 부모 노드를 가리키는 포인터인데, 삽입과 삭제 처리를할때 편리할 뿐더러, 레드블랙트리의 핵심 기능 중 하나인 회전에 필요하기 때문입니다.

레드블랙 트리가 균형을 유지하는 비결

레드블랙트리에는 다소 생소한 규칙이 존재합니다.

  1. 모든 노드는 빨간색 또는 검은색의 색을 가진다.
  2. 루트 노드는 검은색이다.
  3. 잎 노드는 검은색이다.
  4. 빨간 노드의 자식은 모두 검은색이다, 하지만 검은색 노드의 자식이 빨강일 필요는 없다.
    (즉, 레드 노드는 연달아 나타날 수 없으며, 블랙 노드만이 레드 노드의 부모 노드가 될 수 있다)
  5. 루트 노드에서 모든 잎 노드 사이에 존재하는 검은색 노드의 수는 모두 동일하다.


5번 규칙이 이해가 안가실 수 있습니다. 저말은 즉, 모든 잎 노드들은 자신의 위치에서부터 루트까지 올라가는데 만나는 검은색 노드의 수가 같다는 말입니다.
레드 블랙 트리의 잎 노드들은 모두 NIL로 표시되어있네요.이 NIL노드는 아무 데이터도 가지고 있지 않지만, 색깔만 검은색인 더미 노드입니다. 굳이 더미 노드를 할당해가며 사용하는 이유는, 레드블랙트리 구현에 용이하기 때문입니다. 저렇게 하면 "모든 잎 노드는 검은색이다." 라는 규칙은 항상 유지시킬 수 있거든요.

레드블랙 트리의 기본연산

탐색은 기존의 BST의 탐색을 사용하시면 됩니다. 하지만 문제는 노드의 삽입과 삭제에 있습니다. 삽입과 삭제가 이루어지면서 규칙이 무너지게 되거든요. 트리의 균형을 유지하는 규칙이 무너지게 되면 더 이상 레드블랙 트리를 사용할 이유가 없게 되는거죠. 그래서 대부분의 코드가 이 삽입과 삭제를 한뒤에 있는 뒤처리에 관한 것입니다.

회전.

회전은 부모와 자식 노드의 위치를 바꾸는 것입니다. 방향에 따라 우회전과 좌회전으로 나뉩니다. 우회전은 왼쪽 자식과 위치를 바꾸는 것을 말하고 좌회전은 오른쪽 자식과 위치를 바꾸는 것을 말합니다.

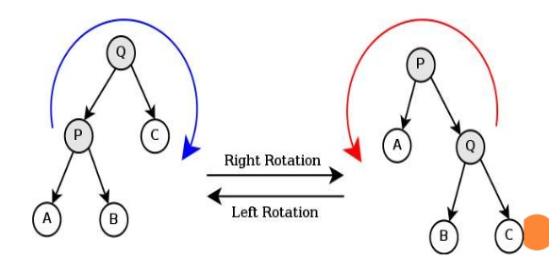
그냥 바꾸면 될 것 같지만, 회전은 그렇게 만만한 친구가 아닙니다.

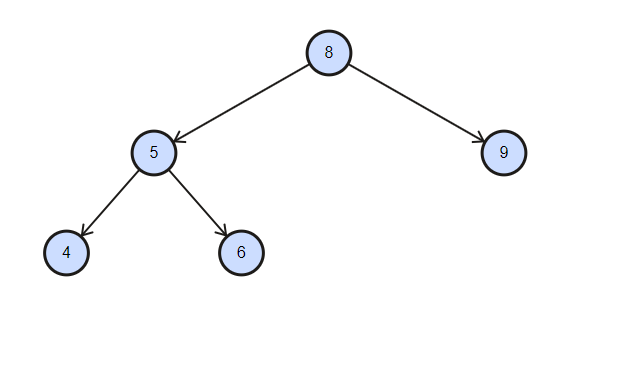
5노드와 8노드를 회전한다고 생각해봅시다.
이진 탐색 트리의 특성상 왼쪽 자식 노드는 부모보다 작고, 오른쪽 자식 노드는 부모보다 커야 하는데, 8노드가 5노드의 왼쪽 자식으로 들어가있습니다. 이렇게 단순히 자식과 부모 둘의 위치만 바꿔버리면 레드블랙 트리의 규칙은 물론 이진 탐색 트리의 규칙 또한 무너지게 되는겁니다.
그렇기 때문에 회전에는 특수한 처리가 같이 따라붙습니다.

우회전을 할 때에는 왼쪽 자식 노드의 오른쪽 자식 노드를 부모 노드의 왼쪽 자식으로 연결시켜줘야합니다. 위 그림에서는 6노드가 8 노드의 왼쪽 자식으로 붙는 겁니다.

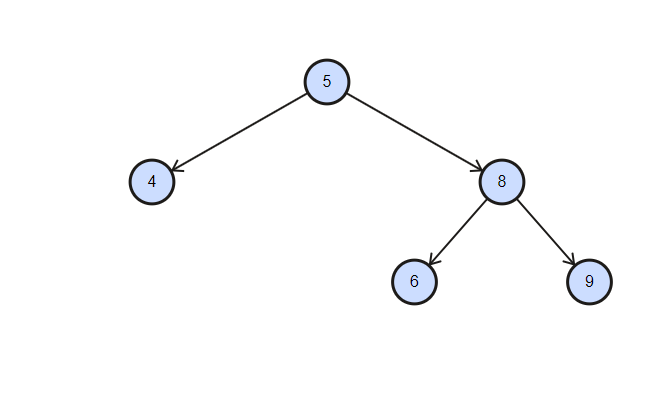
좌회전을 할 때에는 오른쪽 자식 노드의 왼쪽 자식 노드를 부모 노드의 오른쪽 자식으로 연결합니다. 위 그림에서는 6노드가 5 노드의 오른쪽에 붙는겁니다.


그러면 이제 코드를 한번 작성해봅시다 RBT.h 파일을 만들어주세요

//RBT.h
enum Color{ RED, BLACK };

struct RBTNode
{
	struct RBTNode* parent;
	struct RBTNode* left;
	struct RBTNode* right;

	int data;
	enum Color color;
	
};

static RBTNode* NIL;

void RBT_SET();

void RBT_RotateRight(RBTNode** root, RBTNode* parent);
void RBT_RotateLeft(RBTNode** root, RBTNode* parent);

이어서 RBT.c 파일도 만들어봅시다

#include "RBT.h"
#include <stdlib.h>
void RBT_SET()
{
	NIL = (RBTNode*)malloc(sizeof(RBTNode));
	NIL->color = BLACK;
}

void RBT_RotateRight(RBTNode** root, RBTNode* parent)
{
	RBTNode* leftChild = parent->left;

	parent->left = leftChild->right;//왼쪽 자식의 오른쪽 자식 노드를 부모 노드의 왼쪽으로 등록
	
	if (leftChild->right != NIL)
		leftChild->right->parent = parent;

	leftChild->parent = parent->parent;

	if (parent->parent == NULL)//부모가 NULL일 경우 왼쪽 자식을 루트로 변경
		(*root) = leftChild;
	else
	{
		if (parent == parent->parent->left)//왼쪽 자식 노드를 부모가 있던 곳에 위치시킴.
			parent->parent->left = leftChild;
		else
			parent->parent->right = leftChild;
	}
	leftChild->right = parent;
	parent->parent = leftChild;

}

void RBT_RotateLeft(RBTNode** root, RBTNode* parent)
{
	RBTNode* rightChild = parent->right;

	parent->right = rightChild->left;//왼쪽 자식의 오른쪽 자식 노드를 부모 노드의 왼쪽으로 등록

	if (rightChild->left != NIL)
		rightChild->left->parent = parent;

	rightChild->parent = parent->parent;

	if (parent->parent == NULL)//부모가 NULL일 경우 오른쪽 자식을 루트로 변경
		(*root) = rightChild;
	else
	{
		if (parent == parent->parent->right)//오른쪽 자식 노드를 부모가 있던 곳에 위치시킴.
			parent->parent->right = rightChild;
		else
			parent->parent->left = rightChild;
	}
	rightChild->left = parent;
	parent->parent = rightChild;

}

삽입

레드 블랙 트리의 삽입의 기반은 BST와 유사하지만, 다른 면이 있습니다. BST의 경우 탐색한 위치에 값을 삽입하면 그만이지만, 레드블랙 트리는 노드의 삽입 후 무너졌을지 모르는 규칙들을 살펴봐야 합니다.

레드블랙 트리에 노드가 삽입되고 나면, 이 노드를 빨간색으로 칠하고 양쪽 자식에 NIL노드를 붙여줘야 합니다. 그리고 현재 트리가 레드 RBT_InsertNode함수에 이 순서가 들어있습니다.

void RBT_InsertNode(RBTNode** root, RBTNode* newNode)
{
	//BST처럼 재귀를 통해 노드 삽입
	RBT_InsertNodeHelper(root, newNode);

	//새 노드에 색을 칠하고 자식에 NIL을 연결
	newNode->color = RED;
	newNode->left = NIL;
	newNode->right = NIL;

	//무너진 RBT 규칙 조정
	RBT_RebuildAfterInsert(root, newNode);
}

헤더에 RBT_InsertNode함수 및 두개의 함수의 프로토타입을 작성해주세요. 모든 함수의 매개변수는 InsertNode 함수의 매개변수와 동일합니다. RBT_InsertNodeHelper함수는 Parent포인터를 지정해주어야 한다는 것 말고는 BST에서 했던 삽입과 동일합니다. 다만, BuildAfterInsert의 newNode는 이름을 node로 변경해주세요. 후에 있을 처리에서 헷갈릴 수 있습니다.

void RBT_InsertNodeHelper(RBTNode** root, RBTNode* newNode)
{
	RBTNode* tree = (*root);
	if (tree->data < newNode->data)//자식의 값이 루트보다 큰 경우
	{
		if (tree->right == NULL)
		{
			tree->right = newNode;
			newNode->parent = tree;
		}
		else
			RBT_InsertNodeHelper(&tree->right, newNode);
	}
	else if (tree->data > newNode->data)//자식의 값이 루트보다 작은 경우
	{
		if (tree->left == NULL)
		{
			tree->left = newNode;
			newNode->parent = tree;
		}
		else
			RBT_InsertNodeHelper(&tree->left, newNode);
	}
}

간단하죠? 그러면 다시 InsertNode함수로 돌아와서 NIL을 살펴봅시다. 자식에 NIL을 붙여주는 부분을 보다보면 한가지 의문점이 듭니다. 왜 각각의 노드를 할당해주지않고, 전역변수 NIL을 공유해서 쓰는걸까요?
이 이유는 NIL노드는 단순히 구현의 편의를 위해서 도입된 개념으로 실질적으로 데이터를 담는 노드의 역할을 수행하지는 않기 때문입니다. 데이터를 담지도 않는 NIL노드를 여러 개 할당해서 사용하는 것은 비효율적이죠. 그러므로 하나의 전역변수 NIL을 공유해서 사용합니다.

우리은 이제 현재 삽입한 노드가 RBT의 규칙에 맞는지를 검사해야합니다. 규칙을 다시 한번 봅시다.

  1. 모든 노드는 빨간색 또는 검은색의 색을 가진다.
  2. 루트 노드는 검은색이다.
  3. 잎 노드는 검은색이다.
  4. 빨간 노드의 자식은 모두 검은색이다, 하지만 검은색 노드의 자식이 빨강일 필요는 없다.
    (즉, 레드 노드는 연달아 나타날 수 없으며, 블랙 노드만이 레드 노드의 부모 노드가 될 수 있다)
  5. 루트 노드에서 모든 잎 노드 사이에 존재하는 검은색 노드의 수는 모두 동일하다.

지금 상황에서 1,3번 규칙은 절대로 위배될 일이 없습니다. 5번의 규칙 또한 새 노드가 삽입될 때 부모 노드에 연결되어있던 NIL노드를 떼어내고 그 자리에 연결합니다. 그러므로 위반될 수 있는 규칙은.

2.루트 노드는 검은색이다.
4. 빨간 노드의 자식은 모두 검은색이다.

이 두가지로 좁혀집니다. 이 두가지 중에서 "루트 노드는 검은색이다"는 뒤처리가 간단합니다. 루트 노드를 검은색으로 칠해주면 되니까요. 그러면 이제 위반되는 규칙은 딱 하나 남았습니다.

빨간 노드의 자식은 모두 검은색이다

이 규칙이 위반되었다는 것은 삽입한 노드와 부모 노드의 색이 모두 빨간색이라는 사실을 의미합니다. 이 상황은 삽입한 노드의 삼촌, 즉 부모 노드와의 형제 노드가 어떤 색이냐에 따라 그 경우가 세가지로 다시 나뉘어집니다.
참고로 레드블랙트리는 이진트리이기에 삼촌은 하나만 존재할 수 있습니다

1.삼촌도 빨간색인 경우
2.삼촌이 검은색이며 새로 삽입한 노드가 부모 노드의 오른쪽 자식인 경우
3.삼촌이 검은색이며 새로 삽입한 노드가 부모 노드의 왼쪽 자식인 경우

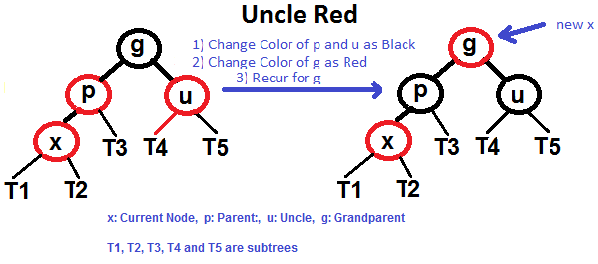
1번 삼촌이 빨간색인 경우에는, 사진처럼 부모와 삼촌을 검은색으로 칠한 후, 할아버지 노드를 빨간색으로 칠하면 됩니다. 이 작업으로 인해 생긴 규칙의 오점은 없는지 다시 한번 살펴봐야 합니다. 할아버지 노드가 빨간색으로 칠해지면서, 할아버지의 할아버지가 빨간색 노드일 경우 또 4번 규칙이 위협받기 때문입니다. 그렇게 계속 타고 올라가 부모 노드가 검은색이거나, 루트 노드에 도달하는 경우까지 검사를 진행해야합니다.

2번의 경우에는 부모 노드를 왼쪽으로 회전시켜, 3번의 상황으로 바꿉니다. 이 방식은 문제의 유형을 바꾼 것이지, 문제가 해결된 것은 아니라는 점을 주의해야 합니다.
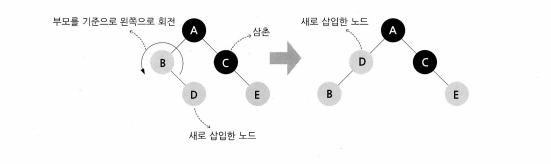(위에 레드블랙 트리는 규칙의 보완을 간략하게 보여드리기 위해 만들어진 트리이지, 정상적인 경우의 레드블랙 트리가 아님을 알려드립니다.)

3번의 경우에는 부모노드를 검은색, 할아버지 노드를 빨간색으로 칠한 후 할아버지 노드를 오른쪽으로 회전시킵니다.

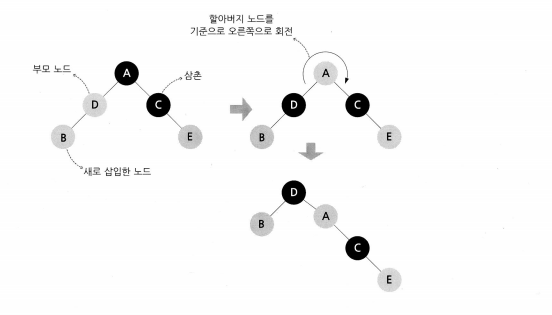
이렇게 처리한 뒤에는 4번 규칙에 위배되지 않습니다. 삽입된 노드 B의 부모가 검은색이기 때문입니다. D의 부모가 빨간색이라고 해도 D가 검은색이기에 4번 규칙에 어긋나지 않습니다.

이 끔찍한 처리를 해주는 코드를 한번 작성해보죠. 

void RBT_RebuildAfterInsert(RBTNode** root, RBTNode* node)
{
	//부모 노드가 루트가 아니거나 빨간색일 경우, while문을 반복한다.
	while (node != (*root) && node->parent->color == RED)
	{

		if (node->parent == node->parent->parent->left)
		{
			//삽입된 노드의 아빠의 아빠의 오른쪽 = 오른쪽 삼촌을 의미한다.
			RBTNode* uncle = node->parent->parent->right;
			if (uncle->color == RED)
			{
				//1번 작업
				node->parent->color = BLACK;
				uncle->color = BLACK;
				node->parent->parent->color = RED;
			}
			else
			{
				//2번 케이스
				if (node == node->parent->right)
				{
					node = node->parent;
					RBT_RotateLeft(root, node);
				}
				node->parent->color = BLACK;
				node->parent->parent->color = RED;
				RBT_RotateRight(root, node->parent->parent);
			}
		}
		else // 위에 있는 구문과 방향만 정반대로 바꾸면 된다.
		{
			//삽입된 노드의 아빠의 아빠의 왼쪽 = 왼쪽 삼촌을 의미한다.
			RBTNode* uncle = node->parent->parent->left;
			if (uncle->color == RED)
			{
				//1번 작업
				node->parent->color = BLACK;
				uncle->color = BLACK;
				node->parent->parent->color = RED;
			}
			else
			{
				//2번 케이스
				if (node == node->parent->left)
				{
					node = node->parent;
					RBT_RotateRight(root, node);
				}
				node->parent->color = BLACK;
				node->parent->parent->color = RED;
				RBT_RotateLeft(root, node->parent->parent);
			}
		}
	}
	(*root)->color = BLACK;
}

코드가 많아서 복잡할 수 있지만, 찬찬히 뜯어보면 그래도 볼만 합니다.

이제 레드블랙 트리의 가장 어려운 문제인 삭제가 남았습니다. 삭제 연산의 경우, 상황의 가짓수로 많을 뿐더러 처리해야 하는 코드의 수도 길기 때문에 이번 강좌에 한번에 나가는 것은 무리라고 생각되어 다음 포스팅으로 미루려고 합니다. 그때까지 회전과 삽입, 리빌딩에 관한 내용을 열심히 복습하자고요!!

해당 글은
"뇌를 자극 하는 알고리즘"
Geeksforgeeks 의 Red Black Tree의 내용을 참고했습니다.

profile
Mr.뉴트리아
뉴트리아는 가시쥐과에 속하는 설치류의 일종이다. 오랫동안 뉴트리아과의 유일종으로 분류했지만, 현재는 가시쥐과에 포함시킨다. 늪너구리, 해리서 또는 코이푸라고도 한다. 뉴트리아는 스페인어로 수달을 의미하고, 출생지 남미에서는 이 종류를 코이푸라고 부른다.
이전 포스트

이진 트리와 이진 탐색 트리

3개의 댓글

comment-user-thumbnail
박시현
2021년 6월 1일

할아버지 노드를 오른쪽으로 회전시켜준 이후에 트리 모형이 5번 규칙에 위배되고 있는것같은데 아닌가요...?

1개의 답글