이진 트리란?
어떠한 것이든, 이름이 왜이렇게 지어졌는지 알아야 한다고 생각합니다.
이진트리, 영어로 binary tree인 이유는 해당 자료구조에 모습에서 따왔습니다.
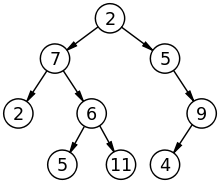
각 노드가 최대 두개의 값을 가질 수 있고,
어때요? 마치 모습이 나무를 뒤집어 놓은 모습과 같지 않나요?
이진 트리에 대해 더 설명을 해드려야겠으나,,,,

자세한 것은 위키피디아가 모두 설명해 줄 것이라 믿습니다.
오늘은 이진 탐색트리를 중요하게 알아볼 것이니까요!
https://ko.wikipedia.org/wiki/%EC%9D%B4%EC%A7%84_%ED%8A%B8%EB%A6%AC
이진트리의 구성
간단하게 이진트리의 구성을 짜보겠습니다.
#include <stdio.h>
#include <stdlib.h>
struct bNode
{
char* data;
bNode* left;
bNode* right;
};
bNode* CreateBinaryNode(const char* str)
{
bNode* node;
if (!(node = (bNode*)malloc(sizeof(bNode))))
return NULL;
node->data = (char *)str;
node->left = NULL;
node->right = NULL;
return (node);
}
void DeleteNode(bNode* node)
{
node->data = NULL;
node->left = NULL;
node->right = NULL;
free(node);
}
void PrintTree(bNode* root, int level)
{
int i = -1;
while (i++ < level)
printf(" ");
printf("%s\n", root->data);
if (root->left)
PrintTree(root->left, level + 1);
if (root->right)
PrintTree(root->right, level + 1);
}
void DestroyTree(bNode* root)
{
if (root->left)
DestroyTree(root->left);
if (root->right)
DestroyTree(root->right);
DeleteNode(root);
}
int main()
{
bNode* node = CreateBinaryNode("A");
bNode* node1 = CreateBinaryNode("B");
bNode* node2 = CreateBinaryNode("C");
bNode* node3 = CreateBinaryNode("D");
bNode* node4 = CreateBinaryNode("E");
node->left = node1;
node->right = node2;
node1->left = node3;
node1->right = node4;
PrintTree(node, 0);
DestroyTree(node);
}한번 컴파일을 돌려볼까요?

나름대로 괜찮게 나옵니다.
이진 탐색 트리란?
위에서 간단하게 이진 트리의 구조를 알아보았습니다. 그러면 이진 탐색 트리는 무엇일까요?
이진 탐색 트리. 영어로는 binary search tree입니다. 여기서 중요한 부분은 "탐색"에 있습니다. 이진 탐색 트리는 어떠한 값을 찾는것에 특화된 자료구조입니다.
즉, '이진 탐색'을 위한 트리이자, 탐색을 위한 '이진 트리'라는 말이 됩니다.
이진 탐색 트리는 이진 트리와 별반 다를게 없지만, 특수한 규칙을 하나 가지고 있습니다.
"왼쪽 자식 노드는 나보다 작고, 오른쪽 자식 노드는 나보다 크다"
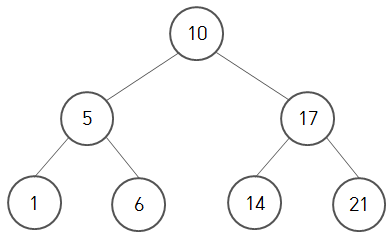
위는 이진 탐색트리의 예시입니다. 보시다시피 왼쪽 자식노드는 부모보다 작고, 오른쪽 자식노드는 부모보다 큰 값을 가지고 있습니다.
이진 탐색 트리의 구성
위에서 만든 이진트리와 별 다를게 없지만, 노드의 삽입 부분이 추가됩니다.
#include <stdio.h>
#include <stdlib.h>
struct bstNode
{
int data;
bstNode* left;
bstNode* right;
};
bstNode* CreateNode(int num)
{
bstNode* node;
if (!(node = (bstNode*)malloc(sizeof(bstNode))))
return NULL;
node->data = num;
node->left = NULL;
node->right = NULL;
return (node);
}
void Insert_Node(bstNode** root, bstNode* child)
{
bstNode* tree = (*root);
if (tree->data < child->data)//자식의 값이 루트보다 큰 경우
{
if (tree->right == NULL)
tree->right = child;
else
Insert_Node(&tree->right, child);
}
else if (tree->data > child->data)//자식의 값이 루트보다 작은 경우
{
if (tree->left == NULL)
tree->left = child;
else
Insert_Node(&tree->left, child);
}
}
void DeleteNode(bstNode* node)
{
node->data = NULL;
node->left = NULL;
node->right = NULL;
free(node);
}
void PrintTree(bstNode* root, int level)
{
int i = -1;
while (i++ < level)
printf(" ");
printf("%d\n", root->data);
if (root->left)
PrintTree(root->left, level + 1);
if (root->right)
PrintTree(root->right, level + 1);
}
void DestroyTree(bstNode* root)
{
if (root->left)
DestroyTree(root->left);
if (root->right)
DestroyTree(root->right);
DeleteNode(root);
}
int main()
{
bstNode* root;
root = CreateNode(30);
Insert_Node(&root, CreateNode(15));
Insert_Node(&root, CreateNode(45));
Insert_Node(&root, CreateNode(70));
Insert_Node(&root, CreateNode(3));
Insert_Node(&root, CreateNode(79));
Insert_Node(&root, CreateNode(64));
Insert_Node(&root, CreateNode(55));
PrintTree(root, 0);
}Insert_Node라는 함수가 새로 생겼습니다. 들어온 child의 값을 판별해서 부모 노드보다 크다면 오른쪽, 작으면 왼쪽 노드로 계속해서 이동시켜, 자식이 없는 노드에 추가시키는 코드입니다.
한번 실행화면을 봐볼까요?

PrintTree에서 왼쪽,오른쪽 순으로 출력했으니까 값이 정상적으로 들어간 것을 확인할 수 있습니다.
그러면 이걸 활용해서 특정 값을 가진 노드를 찾는 함수를 만들어봅시다. 아주 간단해요!
bstNode* Search(bstNode* root, int num)
{
if (root == NULL)
return NULL;
if (root->data == num)
return root;
if (root->left == NULL && root->right == NULL)
{ //자식 노드가 다 없고, 자신이 찾으려는 값이 아닌경우
printf("트리에 찾으려는 값이 없습니다.");
return NULL;
}
if (root->data < num)
return Search(root->right, num);
else
return Search(root->left, num);
}어때요? 생각보다 쉽죠. 그런데 이제 가장 어려운 친구가 남았습니다. "삭제"함수죠.
대개 무언가를 없애는 일이 만드는 것보다 쉬운 편이지만, 자료구조에서는 무언가를 없애는 일이 만드는 일보다 "훨씬" 어렵습니다. 솔직히 말하면, 없애는 일이라기보다는 없애고 난 후에 뒷정리가 어려운 것이죠.
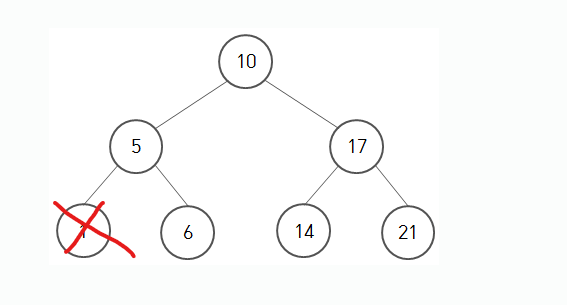
저기 자식이 없는 빨간줄 쳐진 친구(트리에서는 이를 잎 노드라고 부릅니다)를 지우는 것은 괜찮습니다. Search함수로 해당 노드만 제거하면 되니까요. 조금 더 복잡한 경우를 생각해볼까요?
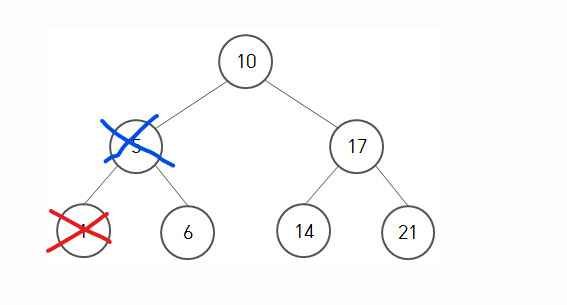
빨간줄 쳐진 노드가 삭제된 후에, 파란줄 쳐진 노드를 지운다고 생각해봅시다. 이 경우도 생각하면 그렇게 어렵지는 않습니다. 6이 들어간 노드를 루트와 연결해주고, 파란 줄 쳐진 노드를 지우면 되는거니까요.
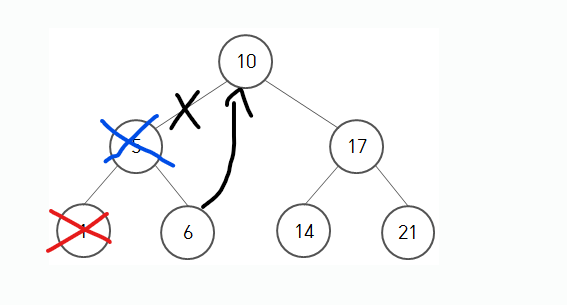
이제 제일 골치아픈 경우를 만나봅시다.
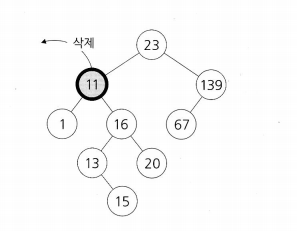
아.... 보기만 해도 머리가 아파옵니다. 그래도 한번 고민을 해봅시다.
11노드가 제거된 빈자리에 어떤 노드를 연결해야할까요?
이진 탐색트리의 규칙을 효율적으로 유지하려면, 어떤 노드를 삭제된 자리에 놓아야할까요?
답은 "삭제될 노드의 오른쪽 하위트리에서 가장 작은 노드 " 입니다.
저 노드의 경우 기존 왼쪽 하위트리의 노드들보다는 크지만, 오른쪽 하위 트리의 노드들보다는 작으니까 중간 노드의 값으로 적합하죠.
이를 최소값 노드라고 지정하겠습니다. 그러면 최소값 노드를 기준으로 하는 함수를 짜봅시다.
bstNode* Remove_Node(bstNode* tree, bstNode* parent, int num)
{
/*
parent라는 매개변수를 하나 더 둔 이유는,
부모 노드쪽에서 자식의 위치를 새로 정해야 하기 때문입니다.
*/
bstNode* rNode = NULL;
if (tree == NULL)
return NULL;
if (tree->data > num)
rNode = Remove_Node(tree->left, tree, num);
else if (tree->data < num)
rNode = Remove_Node(tree->right, tree, num);
else//삭제할 값을 찾은 경우
{
rNode = tree;
if (tree->left == NULL && tree->right == NULL)
{ //잎 노드인 경우 바로 삭제
if (parent->left == tree)
parent->left = NULL;
else
parent->right = NULL;
}
else
{
//자식이 둘다 있는 경우
if (tree->left != NULL && tree->right != NULL)
{
bstNode* minNode = tree->right;
while (minNode->left != NULL)
minNode = minNode->left;
rNode = Remove_Node(tree, NULL, minNode->data);
tree->data = minNode->data;
}
else//자식이 하나인 경우
{
bstNode* temp = NULL;
if (tree->left != NULL)
temp = tree->left;
else
temp = tree->right;
if (parent->left == tree)
parent->left = temp;
else
parent->right = temp;
}
}
}
return rNode;
}후... 드디어 끝이 났습니다. 그러면 한번 써볼까요?
int main()
{
bstNode* root;
root = CreateNode(23);
Insert_Node(&root, CreateNode(11));
Insert_Node(&root, CreateNode(1));
Insert_Node(&root, CreateNode(16));
Insert_Node(&root, CreateNode(13));
Insert_Node(&root, CreateNode(20));
Insert_Node(&root, CreateNode(15));
Insert_Node(&root, CreateNode(139));
Insert_Node(&root, CreateNode(67));
PrintTree(root, 0);
}remove함수를 쓰기 전 트리 구조입니다.
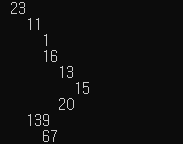
그러면 이제 Remove_Node 함수를 써볼까요?
int main()
{
bstNode* root;
root = CreateNode(23);
Insert_Node(&root, CreateNode(11));
Insert_Node(&root, CreateNode(1));
Insert_Node(&root, CreateNode(16));
Insert_Node(&root, CreateNode(13));
Insert_Node(&root, CreateNode(20));
Insert_Node(&root, CreateNode(15));
Insert_Node(&root, CreateNode(139));
Insert_Node(&root, CreateNode(67));
//Remove_Node는 구조 상 지울 노드를 반환하는 함수이기에
//추가적으로 함수를 제거해주어야 합니다.
DeleteNode(Remove_Node(root, root, 11));
PrintTree(root, 0);
}
효과적으로 11노드가 제거되고, 13노드의 하위 노드로 16이 올라온 것을 확인할 수 있습니다.
이진 트리의 문제점.....
언뜻 보면 이진트리가 완전무결의 자료구조같지만, 실은 엄청난 문제가 하나 있습니다. 탐색의 시간이 트리의 모양과 직결된다는 것이죠. 간혹 트리가 한쪽 방향으로만 길어 늘어져 있다면, 탐색의 효율을 극단적으로 떨어트릴 수 있습니다. 밑에 나온 이진 탐색트리가 그 예입니다.
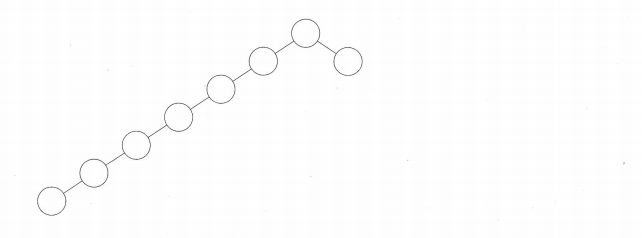
그리고 현실에서는 꽤나 이런상황이 많이 발생할 여지가 존재합니다. 예를 들어봅시다. mmorpg에서 어떤 보스의 타임어택 시간을 이진 탐색트리로 구현한다고 생각해봅시다. 처음에는 유저들의 스펙이 평균적이니까 어느정도 균형잡힌 트리가 유지될껍니다. 하지만 1년..2년... 업데이트가 진행되면 진행될수록 유저들의 스펙은 올라가 있을것이고, 점점 왼쪽으로 쏠리는 모양의 트리가 나올겁니다.
이럴 거면 그냥 리스트를 쓰고말지
이런 문제를 해결하기 위해 레드 블랙 트리라는 것이 존재합니다. 그건 나중에 알아봅시다.
