문제

https://www.acmicpc.net/problem/1285

N^2개의 동전이 N행 N열을 이루어 탁자 위에 놓여 있다. 그 중 일부는 앞면(H)이 위를 향하도록 놓여 있고, 나머지는 뒷면(T)이 위를 향하도록 놓여 있다. <그림 1>은 N이 3일 때의 예이다.

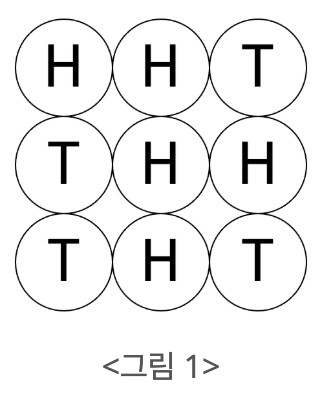
이들 N^2개의 동전에 대하여 임의의 한 행 또는 한 열에 놓인 N개의 동전을 모두 뒤집는 작업을 수행할 수 있다. 예를 들어 <그림 1>의 상태에서 첫 번째 열에 놓인 동전을 모두 뒤집으면 <그림 2>와 같이 되고, <그림 2>의 상태에서 첫 번째 행에 놓인 동전을 모두 뒤집으면 <그림 3>과 같이 된다.

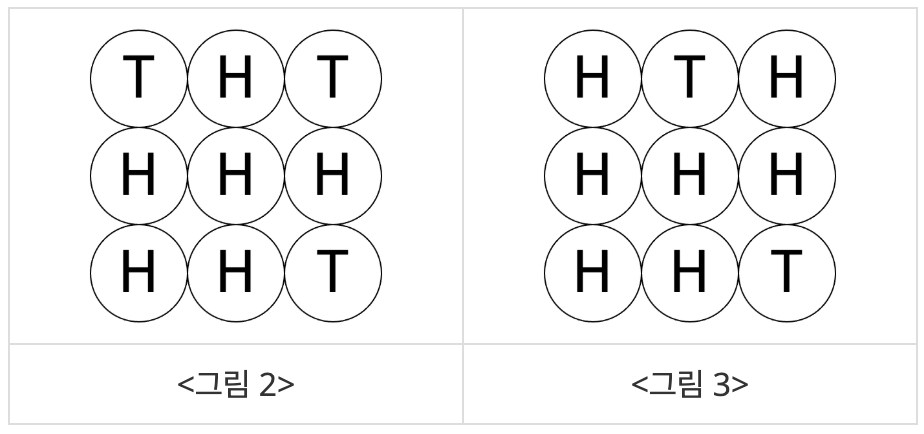
<그림 3>의 상태에서 뒷면이 위를 향하여 놓인 동전의 개수는 두 개이다. <그림 1>의 상태에서 이와 같이 한 행 또는 한 열에 놓인 N개의 동전을 모두 뒤집는 작업을 계속 수행할 때 뒷면이 위를 향하도록 놓인 동전의 개수를 2개보다 작게 만들 수는 없다.

N^2개의 동전들의 초기 상태가 주어질 때, 한 행 또는 한 열에 놓인 N개의 동전을 모두 뒤집는 작업들을 수행하여 뒷면이 위를 향하는 동전 개수를 최소로 하려 한다. 이때의 최소 개수를 구하는 프로그램을 작성하시오.

접근

당연히 안 될 걸 알지만 완전 탐색으로 한 번 해봤다가 시간 초과를 봤고ㅎ...
그리디 문제라길래 T가 더 많은 행이나 열만 다 뒤집으면 되나? 생각했는데 또 그러자니 매 시행마다 모든 행과 열을 확인하는 것도 오버헤드가 클 것 같았다. 확인했다고 해도 하나를 뒤집으면 다른 행, 열의 T 개수에 영향을 주게 되니까 썩 맞는 풀이 같지 않아서.. 다른 블로그에서 풀이 방식을 약간 참고했다.

행만 뒤집거나, 열만 뒤집을 때는 각 뒤집기가 독립적이기 때문에 문제가 없다. 그런데 행을 뒤집었다가 열을 뒤집었다가 또 행을 뒤집었다가 하는 순간 문제가 생기는 거다.
그러니까 일단 행을 뒤집을 수 있는 모든 경우의 수를 다 구해서 행은 딱 고정을 시킨 상태로 각 열들을 순회하며 T의 개수가 더 많은 열을 뒤집으면 문제가 해결된다. 어차피 N의 최댓값이 20으로 매우 작기 때문에 행을 뒤집을 수 있는 모든 경우의 수를 다 구하는 브루트포스를 적용해도 시간 초과가 나지 않는다.
(문제를 보고 시간 내에 이런 접근 방식을 떠올릴 자신이 아직까진 솔직히 없다....)

구현

행을 뒤집을 수 있는 모든 경우의 수를 어떻게 탐색할 것인가에 따라 백트래킹으로도, 비트마스킹으로도 구현할 수 있다.

백트래킹을 이용한 구현

행을 뒤집을 수 있는 모든 경우를 백트래킹을 통해 탐색하는 풀이이다.

import java.io.*;

class Main {
    static int N;
    static boolean[][] isHead;
    static int result = 400;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        isHead = new boolean[N][N];
        for (int i = 0; i < N; i++) {
            String input = br.readLine();
            for (int j = 0; j < input.length(); j++) {
                isHead[i][j] = (input.charAt(j) == 'H');
            }
        }

		// limit: 뒤집을 행의 총 개수. (0개~N개)
        for (int limit = 0; limit <= N; limit++) {
            dfs(0, 0, limit);
        }
    }

    private static void dfs(int bit, int rowNum, int limit) {
    	// 모든 행에 대해 탐색이 끝난 경우 종료
        if (rowNum == N) {
            return;
        }
		
        // limit개만큼의 행이 모두 선택되었다면 getSum() 호출해 T의 개수 구하고 종료
        if (Integer.bitCount(bit) == limit) {
            result = Math.min(result, getSum());
            return;
        }

		// rowNum번째 행을 선택하지 않고 다음 행으로 이동해 탐색
        dfs(bit, rowNum + 1, limit);
		
        // rowNum번째 행 선택 -> 뒤집기
        changeRow(rowNum);
        // rowNum번째 행 마스킹
        bit |= (1 << rowNum);
        // rowNum번째 행을 선택한 상태로 다음 행으로 이동해 탐색
        dfs(bit, rowNum + 1, limit);
        // rowNum번째 행을 뒤집은 경우에 대한 탐색이 끝나면 해당 행을 다시 원래대로 되돌리기
        changeRow(rowNum);
    }

    private static void changeRow(int rowNum) {
    	// isHead[rowNum][col]의 값을 반전시킴.
        for (int col = 0; col < N; col++) {
            isHead[rowNum][col] = !(isHead[rowNum][col] == true);
        }
    }

    private static int getSum() {
        int sum = 0;
        for (int col = 0; col < N; col++) {
            int headCount = 0;
            for (int row = 0; row < N; row++) {
                if (isHead[row][col]) {
                    headCount++;
                }
            }
            // 현재 열에 H의 개수가 더 많다면 뒤집지 않고 현재 T의 개수 (N-headCount)를 취하기.
            // 현재 열에 T의 개수가 더 많다면 뒤집어서 현재 H의 개수를 취하기.
            sum += Math.min(headCount, N - headCount);
        }
        return sum;
    }
}

비트마스밍을 이용한 구현

각 행을 그대로 두거나 혹은 뒤집거나 하는 두 가지의 상태만 존재하기 때문에, 각 경우의 수를 비트마스킹으로 나타낼 수도 있다.
예를 들어, N이 5이고 비트가 10011로 마스킹이 되어 있다면 0번째, 3번째, 4번째 행을 뒤집었다는 뜻이 된다.

import java.io.*;

class Main {
    static int N;
    static boolean[][] isHead;
    static int result = 400;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        isHead = new boolean[N][N];
        for (int i = 0; i < N; i++) {
            String input = br.readLine();
            for (int j = 0; j < input.length(); j++) {
                isHead[i][j] = (input.charAt(j) == 'H');
            }
        }
	
    	// 행을 선택하는 모든 경우의 수 순회
        for (int bit = 0; bit < (1 << N); bit++) {
            int sum = 0;
            for (int col = 0; col < N; col++) {
                int headCount = 0;
                for (int row = 0; row < N; row++) {
                	// 현재 위치가 T이지만 행이 반전된 상태인 경우 -> 현재 H라는 뜻.
                    if (((bit & (1 << row)) != 0 && !isHead[row][col])
                    // 현재 위치가 H이고 행이 반전되지 않은 경우. -> 현재 H라는 뜻.
                    || ((bit & (1 << row)) == 0 && isHead[row][col])) {
                    	// H의 개수를 1 증가
                        headCount++;
                    }
                }
                // 현재 열에 H의 개수가 더 많다면 뒤집지 않고 현재 T의 개수 (N-headCount)를 취하기.
            	// 현재 열에 T의 개수가 더 많다면 뒤집어서 현재 H의 개수를 취하기.
                sum += Math.min(headCount, N - headCount);
            }
            result = Math.min(result, sum);
        }

        System.out.println(result);
    }
}

정말 놀랍게도 비트마스킹을 사용한 풀이가 훨씬 느렸다.

if (((bit & (1 << row)) != 0 && !isHead[row][col])
    || ((bit & (1 << row)) == 0 && isHead[row][col])) {
    headCount++;
 }

위 조건문을 반복하는 오버헤드가 생각보다 큰 것 같다.