BOJ 13334 철로 (Java)

사람·2025년 9월 4일

BOJ

목록 보기

64/74

문제

https://www.acmicpc.net/problem/13334

집과 사무실을 통근하는 n명의 사람들이 있다. 각 사람의 집과 사무실은 수평선 상에 있는 서로 다른 점에 위치하고 있다. 임의의 두 사람 A, B에 대하여, A의 집 혹은 사무실의 위치가 B의 집 혹은 사무실의 위치와 같을 수 있다. 통근을 하는 사람들의 편의를 위하여 일직선 상의 어떤 두 점을 잇는 철로를 건설하여, 기차를 운행하려고 한다. 제한된 예산 때문에, 철로의 길이는 d로 정해져 있다. 집과 사무실의 위치 모두 철로 선분에 포함되는 사람들의 수가 최대가 되도록, 철로 선분을 정하고자 한다.

양의 정수 d와 n 개의 정수쌍, (hi, oi), 1 ≤ i ≤ n,이 주어져 있다. 여기서 hi와 oi는 사람 i의 집과 사무실의 위치이다. 길이 d의 모든 선분 L에 대하여, 집과 사무실의 위치가 모두 L에 포함되는 사람들의 최대 수를 구하는 프로그램을 작성하시오.

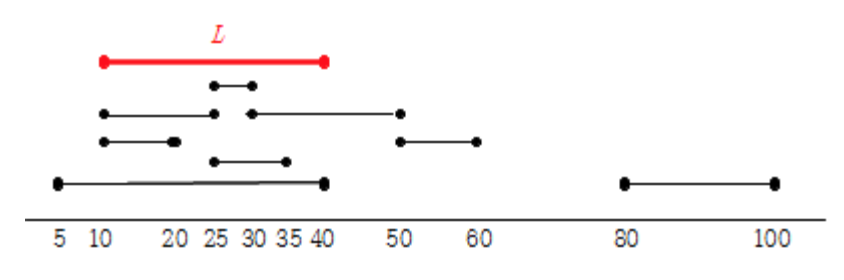
그림 1. 8 명의 집과 사무실의 위치

그림 1 에 있는 예를 고려해보자. 여기서 n = 8, (h1, o1) = (5, 40), (h2, o2) = (35, 25), (h3, o3) = (10, 20), (h4, o4) = (10, 25), (h5, o5) = (30, 50), (h6, o6) = (50, 60), (h7, o7) = (30, 25), (h8, o8) = (80, 100)이고, d = 30이다. 이 예에서, 위치 10 과 40 사이의 빨간색 선분 L이, 가장 많은 사람들에 대하여 집과 사무실 위치 모두 포함되는 선분 중 하나이다. 따라서 답은 4 이다.

입력
입력은 표준입력을 사용한다. 첫 번째 줄에 사람 수를 나타내는 양의 정수 n (1 ≤ n ≤ 100,000)이 주어진다. 다음 n개의 각 줄에 정수 쌍 (hi, oi)가 주어진다. 여기서 hi와 oi는 −100,000,000이상, 100,000,000이하의 서로 다른 정수이다. 마지막 줄에, 철로의 길이를 나타내는 정수 d (1 ≤ d ≤ 200,000,000)가 주어진다.

출력
출력은 표준출력을 사용한다. 길이 d의 임의의 선분에 대하여, 집과 사무실 위치가 모두 그 선분에 포함되는 사람들의 최대 수를 한 줄에 출력한다.

예제 입력 1
8
5 40
35 25
10 20
10 25
30 50
50 60
30 25
80 100
30
예제 출력 1
4

예제 입력 2
4
20 80
70 30
35 65
40 60
10
예제 출력 2
0

예제 입력 3
5
-5 5
30 40
-5 5
50 40
5 -5
10
예제 출력 3
3

슬라이딩 윈도우 이용

접근

예전에 풀다가 너무 열받아서 때려쳤던 2018 카카오 신입 공채 1차 추석 트래픽 문제랑 비슷한 느낌인 것 같다고 생각했다.
결국 그 문제를 제대로 못 풀긴 했지만 해설에서 윈도우를 사용해 풀 수 있다고 했던 걸 봤던 기억이 있어서 이 문제도 그런 식으로 접근해봤다. 좌표 전체 범위 내에서 윈도우를 1씩 이동시키면서 윈도우에 들어오는 입력은 넣고, 범위에서 벗어난 입력은 빼는 식이다.
h와 o 중 더 작은 값을 start, 더 큰 값을 end라고 해보자.

윈도우 범위 내에 들어온 새로운 원소 추가
문제에 따르면 start와 end 값 둘 다 철로 선분 안에 들어와 있어야 유효한 상태이기 때문에 end 값까지 윈도우 안에 들어와야 유효한지 판단할 가치가 생긴다. 그래서 아직 윈도우 안에 안 들어오고 대기 중인 입력들을 waiting이라는 우선순위 큐에 넣어두고, end 값이 작을수록 높은 우선순위를 갖도록 했다. 윈도우를 1 이동시킬 때마다 waiting에 있는 입력들 중 end 값이 윈도우 내에 있는 애들을 차례로 하나씩 확인하고, start까지 윈도우 내에 있으면 inRange(현재 윈도우에 있는 입력들을 저장하는) 우선순위 큐에 넣었다. start 값이 윈도우를 벗어나 있으면 그냥 버리고.
윈도우 범위에서 벗어난 원소 삭제
inRange 내에서는 end 값이 아직 윈도우 범위 내에 있더라도 start 값이 윈도우를 벗어났다면 더 이상 유효하지 않다. 따라서 inRange는 start 값이 작을수록 높은 우선순위를 갖도록 했다. 윈도우를 1 이동시킬 때마다 inRange에 있는 입력들을 하나씩 확인하고, start 값이 윈도우를 벗어났다면 inRange에서 삭제했다.

위와 같은 식으로 우선순위 큐 2개를 이용해 구현을 했다.

구현

import java.io.*;
import java.util.*;

class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        PriorityQueue<Route> waiting = new PriorityQueue<>((r1, r2) -> r1.end - r2.end);
        int under = Integer.MAX_VALUE;
        int upper = Integer.MIN_VALUE;
        for (int i = 0; i < n; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int h = Integer.parseInt(st.nextToken());
            int o = Integer.parseInt(st.nextToken());
            if (h < o) {
                under = Math.min(under, h);
                upper = Math.max(upper, o);
            } else {
                under = Math.min(under, o);
                upper = Math.max(upper, h);
            }
            waiting.offer(new Route(h, o));
        }

        int d = Integer.parseInt(br.readLine());
        PriorityQueue<Route> inRange = new PriorityQueue<>((r1, r2) -> r1.start - r2.start);
        while (!waiting.isEmpty()) {
            Route next = waiting.peek();
            if (next.end > under + d) {
                break;
            }
            waiting.poll();
            if (next.start >= under) {
                inRange.offer(next);
            }
        }
        int result = inRange.size();
        for (int i = under + 1; i + d <= upper; i++) {
        	// 윈도우를 벗어난 입력 제거
            while (!inRange.isEmpty() && inRange.peek().start < i) {
                inRange.poll();
            }
            // 새롭게 윈도우에 추가된 입력을 inRange에 추가
            while (!waiting.isEmpty()) {
                Route next = waiting.peek();
                if (next.end > i + d) {
                    break;
                }
                waiting.poll();
                if (next.start >= i) {
                    inRange.offer(next);
                }
            }
            result = Math.max(result, inRange.size());
        }

        System.out.println(result);
    }

    static class Route {
        int start;
        int end;
        Route (int h, int o) {
            if (h < o) {
                this.start = h;
                this.end = o;
            } else {
                this.start = o;
                this.end = h;
            }
        }
    }
}

시간 복잡도

이렇게 해서 정답 처리되긴 했는데,

java 11로 제출한 사람 중 뒤에서 3등이라는 좀 불미스러운 실행 시간이 나왔다.

시간 복잡도를 생각해보면 윈도우 좌표를 1씩 이동시키고, 그때마다 우선순위 큐의 힙 연산(O(logN))을 수행하기 때문에 최종적으로 O((좌표범위) log n)이 된다.
문제에서 주어진 좌표 범위의 최솟값은 -1억, 최댓값은 +1억이기 때문에 최악의 경우 시간 복잡도가 O(2억logN)이 될 수도 있다.
그래서 시간 복잡도를 개선할 수 있는 다른 풀이를 찾아보았고, 그것이 아래에 있는 스위핑을 이용한 풀이이다.

스위핑 이용

접근

나는 윈도우를 한 칸씩 밀며 모든 가능한 철로 선분의 경우를 다 확인했는데, 사실 그럴 필요가 없었다.
왜냐하면 이 문제에서 윈도우 내 원소 개수가 바뀌는 지점은 어떤 입력 선분이 끝나는 순간에 한정되어 있기 때문이다. 철도 선분의 끝점이 변할 때만 윈도우 포함 여부가 달라지는 것이다. 그렇기 때문에 각 입력별 end 값을 윈도우 끝 경계로 하는 경우만 확인을 해줘도 충분하다.
그러니까 기본적인 흐름은 다음과 같다.

입력쌍 중 start와 end 사이의 거리가 d를 초과하는 입력은 미리 버린다.
입력을 end 값을 기준으로 오름차순 정렬해 리스트에 저장한다.
리스트에 저장된 입력을 하나씩 확인한다.
현재 확인하고 있는 입력을 기준으로 [end - d, end]라는 윈도우 사이에 몇 개의 집과 사무실 쌍이 있는지를 확인한다. (end값으로부터 스위핑)

1번에서 입력을 end 값 기준으로 오름차순 정렬하는 이유가 3번에서[end - d, end] 사이에 있는 입력쌍의 개수를 찾기 위함이다. 입력이 end 값 기준 오름차순 정렬되어 있으니 앞에서 확인한 입력은 현재 확인하고 있는 입력보다 end 좌표가 더 앞에 있었을 것이고, 이후에 확인할 입력은 end 좌표가 더 뒤에 있을 것이다.
그러니 [end - d, end] 범위 내의 입력들은 이전에 확인한 입력쌍들 중에 있을 것이다.

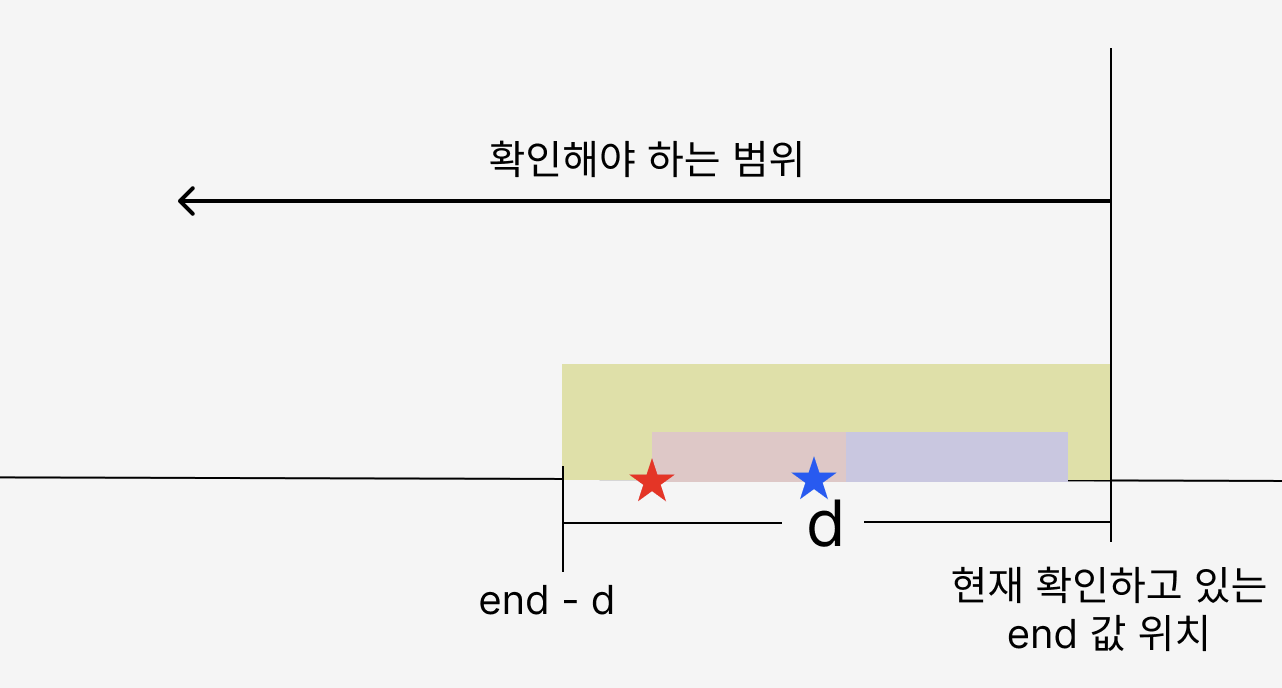
이전에 확인한 입력쌍들 중에서도 start 값 역시 이 범위 내에 있는 입력이라면 윈도우 범위 내에 있음을 알 수 있다. 위 사진에서 별 표시된 부분이 이전에 확인한 입력의 start 값이다. 두 start 값 모두 범위 내에 있고, 이전에 확인한 입력이니 end 값도 당연히 현재 end 값보다 작을 수밖에 없기에 현재 윈도우 내에 있는 입력쌍임을 알 수 있다.

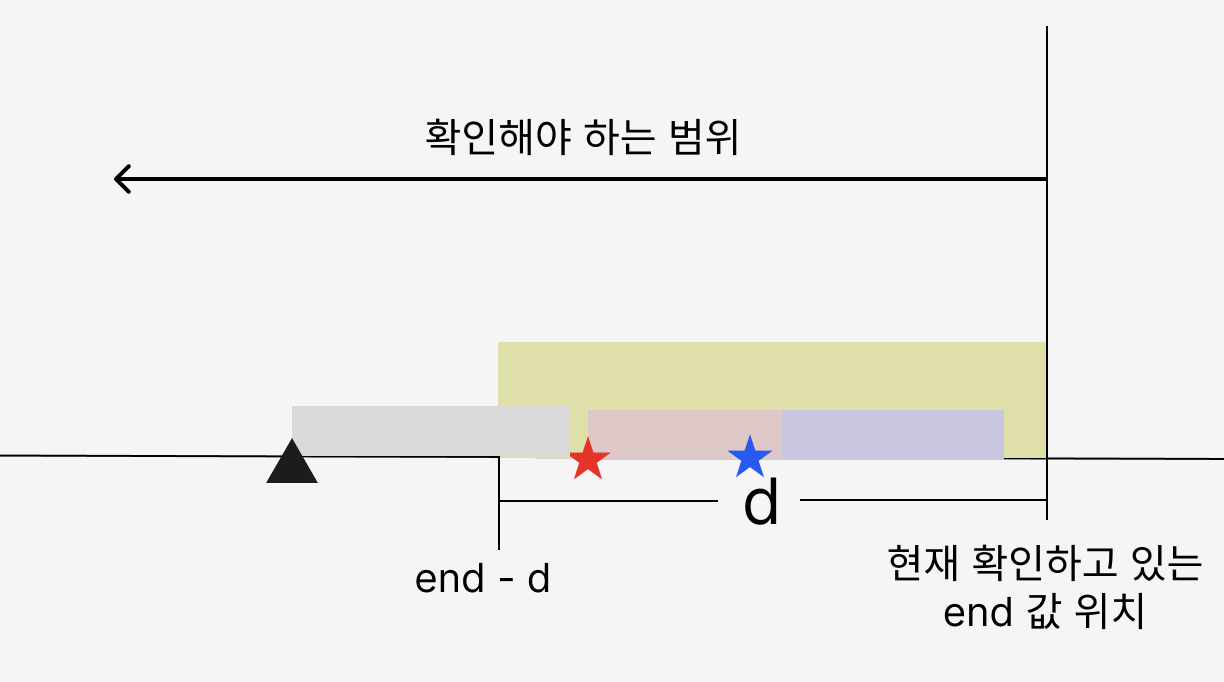
end 값은 리스트를 순회할수록 커지기 때문에, 윈도우도 점점 뒤로 간다. 그러니 한 번 start 범위를 벗어난 입력이 다시 윈도우 내로 돌아올 수는 없다. 위 사진에서 세모에 해당하는 start 값은 윈도우 범위를 벗어났기 때문에 end 값이 범위 내에 있는지와 상관 없이 이후에도 더 이상 유효할 수 없다. 따라서 이 입력은 제거해주면 된다.

정리하면, 이후에 확인하게 될 입력쌍들은 신경을 안 써도 되고, 이전에 확인한 입력쌍들 중에서 start 값이 범위 내에 있는 게 몇 개인지만 확인하면 된다. 이를 위해서는 이미 확인한 입력쌍의 start 값만을 우선순위 큐에 저장하고, start 값이 작은 순으로 하나씩 확인하며 그 값이 [end - d, end] 범위에 있는지 확인하면 될 것이다.

구현

import java.io.*;
import java.util.*;

class Main {
    static class Interval {
        int s, e;
        Interval(int a, int b) {
            if (a <= b) { s = a; e = b; }
            else { s = b; e = a; }
        }
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());

        List<Interval> list = new ArrayList<>(n);
        for (int i = 0; i < n; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int h = Integer.parseInt(st.nextToken());
            int o = Integer.parseInt(st.nextToken());
            list.add(new Interval(h, o));
        }
        int d = Integer.parseInt(br.readLine());

        // 길이 d 초과는 제거
        List<Interval> cand = new ArrayList<>();
        for (Interval it : list) {
            if (it.e - it.s <= d) cand.add(it);
        }
        if (cand.isEmpty()) {
            System.out.println(0);
            return;
        }

        // end 오름차순, tie 시 start 오름차순
        cand.sort((a, b) -> {
            if (a.e != b.e) return Integer.compare(a.e, b.e);
            return Integer.compare(a.s, b.s);
        });

        PriorityQueue<Integer> pq = new PriorityQueue<>(); // 시작점 최소힙
        int ans = 0;
        for (Interval it : cand) {
            pq.offer(it.s);
            int threshold = it.e - d;
            while (!pq.isEmpty() && pq.peek() < threshold) {
                pq.poll();
            }
            ans = Math.max(ans, pq.size());
        }
        System.out.println(ans);
    }
}

시간 복잡도

앞서 설명했듯 확인해야 하는 경우의 수가 입력의 개수로 한정된다. 그리고 각 입력에 대해 우선순위 큐의 힙 연산(O(logN))을 수행한다.
따라서 최종적인 시간 복잡도는 O(nlogN)이 된다. 여기서 n은 입력 값의 개수인데, 슬라이딩 윈도우를 사용했을 때에는 logN에 곱해지는 값이 최악의 경우 2억까지 될 수 있는 반면 n은 최대 10만에 불과하므로 보다 효율적이라고 할 수 있다.