문제

https://www.acmicpc.net/problem/22866

일직선으로 다양한 높이의 건물이 총
$N$개가 존재한다. 각 건물 옥상에서 양 옆에 존재하는 건물의 옆을 몇 개 볼 수 있는지 궁금해졌다.

$i$번째 건물 기준으로
$i - 1$,
$i - 2$, ...,
$1$번째 건물은 왼쪽에,
$i + 1$,
$i + 2$, ...,
$N$번째 건물은 오른쪽에 있다. 각 건물 사이의 거리는 다 동일하다.

현재 있는 건물의 높이가
$L$이라고 가정하면 높이가
$L$보다 큰 곳의 건물만 볼 수 있다.

바라보는 방향으로 높이가
$L$인 건물 뒤에 높이가
$L$이하인 건물이 있다면 가려져서 보이지 않는다.

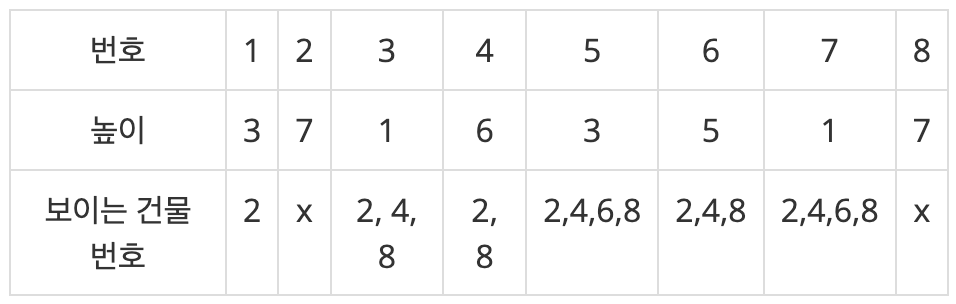
각 건물에서 볼 수 있는 건물들이 어떤것이 있는지 구해보자.

입력
첫번째 줄에 건물의 개수
$N$이 주어진다.

두번째 줄에는
$N$개의 건물 높이가 공백으로 구분되어 주어진다.

출력
$i(1 \le i \le N)$번째 건물에서 볼 수 있는 건물의 개수를 출력한다.

만약 볼 수 있는 건물의 개수가 1개 이상이라면
$i$번째 건물에서 거리가 가장 가까운 건물의 번호 중 작은 번호로 출력한다.

제한
$1 \le N \le 100,000$ 
$1 \le L \le 100,000$ 

예제 입력 1
8
3 7 1 6 3 5 1 7
예제 출력 1
1 2
0
3 2
2 2
4 4
3 4
4 6
0
3번째 건물에서 볼 수 있는 건물은 2, 4, 8번째 건물로 총 3개를 볼 수 있다. 그 중 3번째 건물과 가장 가까운 건물은 2, 4번째 있는 건물로 이 중 번호가 작은 번호인 2가 답이 된다.

접근

일단 누가 봐도 단조 스택 문제였는데, 약간의 응용이 필요했다.

1. 왼쪽 방향과 오른쪽 방향을 모두 고려해야 함.
2. 현재 건물에서 볼 수 있는 건물의 개수를 모두 찾아야 함.

일단 1번의 경우 왼쪽에서 오른쪽으로, 오른쪽에서 왼쪽으로 총 2번 배열을 순회한 후 두 결과를 합하면 될 거라고 생각했다.
2번에서 약간 고민을 했다. 지금까지 봤던 단조 스택 문제는 자신보다 높이가 높으면서 가장 가까운 건물을 찾으면 끝이었는데, 이 문제는 현재 건물에서 가려지지 않고 보이는 모든 건물의 수를 구해야 했기 때문이었다.

1차 시도 (시간 초과)

내가 생각해낸 방법은, 일단 일반적인 단조 스택 문제에서 했던 것처럼 자신보다 높이가 높으면서 가장 가까운 건물을 찾은 다음, 체인을 돌듯이 그 뒤에 보이는 건물을 찾는 거였다.

단조 스택을 통해 자신보다 높이가 높으면서 가장 가까운 건물을 찾는 방법은 다음과 같다.

1. 건물의 높이가 저장된 배열을 차례대로 순회한다.
   • 왼쪽 -> 오른쪽으로 순회 시 자신의 오른쪽 방향에 있는 건물들만 확인.
   • 오른쪽 -> 왼쪽으로 순회 시 자신의 왼쪽 방향에 있는 건물들만 확인.
2. 스택이 비어 있거나, 스택 맨 위에 있는 건물의 높이가 현재 건물의 높이보다 낮으면 스택에 현재 건물 번호를 push한다.
3. 스택 맨 위에 있는 건물의 높이가 현재 건물의 높이보다 높거나 같으면 작아질 때까지 스택에서 pop한다.
   • 현재 건물이 pop된 건물보다 높으면서 가장 가까이 있는 건물이 된다.
4. pop이 모두 완료되면 현재 건물 번호를 스택에 push 한다.

문제에 주어진 테스트 케이스로 예를 들어보자. 일단 자신보다 오른쪽에 있는 건물들만 본다고 가정하고 왼쪽 -> 오른쪽으로 순회하면 다음과 같은 결과가 나온다.

번호	높이	자신의 오른쪽에 보이는 가장 가까운 건물 번호
1	3	2
2	7	없음 (0)
3	1	4
4	6	8
5	3	6
6	5	8
7	1	8
8	7	없음 (0)

3번 건물에서 오른쪽을 봤을 때, 몇 개의 건물을 볼 수 있을까?
일단 3번 건물에서 볼 수 있는 가장 가까운 건물은 4번이다.
그리고 4번 건물에서 볼 수 있는 가장 가까운 건물은 8번이다.
8번 건물에서는 더 이상 볼 수 있는 건물이 없다.
이렇게 3번 건물에서 시작해 0이 나올 때까지 가장 가까운 건물 번호를 계속 타고 들어가면 3 -> 4 -> 8, 총 2개의 건물이 보임을 알 수 있는 것이다.

같은 방식으로 오른쪽 -> 왼쪽으로 순회해 왼쪽에 보이는 건물의 수도 구하고, 두 결과를 서로 더하면 양 방향에서 보이는 모든 건물 개수를 구할 수 있다.

import java.io.*;
import java.util.*;

class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        StringBuilder sb = new StringBuilder();
        int[] heights = new int[N + 1];
        int[] rightClosest = new int[N + 1];
        int[] leftClosest = new int[N + 1];
        int[] counts = new int[N + 1];
        String[] input = br.readLine().split(" ");
        
        for (int i = 1; i <= N; i++) {
            heights[i] = Integer.parseInt(input[i - 1]);
        }

        Stack<Integer> stack = new Stack<>();
        for (int i = 1; i <= N; i++) {
            if (stack.isEmpty() || heights[stack.peek()] >= heights[i]) {
                stack.push(i);
                continue;
            }
            while (!stack.isEmpty() && heights[stack.peek()] < heights[i]) {
                int num = stack.pop();
                rightClosest[num] = i;
            }
            stack.push(i);
        }

        stack = new Stack<>();
        for (int i = N; i > 0; i--) {
            if (stack.isEmpty() || heights[stack.peek()] >= heights[i]) {
                stack.push(i);
                continue;
            }
            while (!stack.isEmpty() && heights[stack.peek()] < heights[i]) {
                int num = stack.pop();
                leftClosest[num] = i;
            }
            stack.push(i);
        }

        for (int i = 1; i <= N; i++) {
            int idx = i;
            while (rightClosest[idx] > 0) {
                counts[i]++;
                idx = rightClosest[idx];
            }
            idx = i;
            while (leftClosest[idx] > 0) {
                counts[i]++;
                idx = leftClosest[idx];
            }
        }

        for (int i = 1; i <= N; i++) {
            if (counts[i] == 0) {
                sb.append(0);
            } else if (leftClosest[i] == 0) {
                sb.append(counts[i]).append(' ').append(rightClosest[i]);
            } else if (rightClosest[i] == 0) {
                sb.append(counts[i]).append(' ').append(leftClosest[i]);
            } else if (rightClosest[i] - i < i - leftClosest[i]) {
                sb.append(counts[i]).append(' ').append(rightClosest[i]);
            } else {
                sb.append(counts[i]).append(' ').append(leftClosest[i]);
            }
            sb.append('\n');
        }

        System.out.print(sb.toString());
    }
}

하지만 이 방식은 80%쯤에서 시간 초과가 났다.
자신보다 높으면서 가장 가까운 건물을 계속 타고 타고 들어가야 하다 보니 그 체인의 깊이가 깊어지는 경우에는 $O(N^2)$까지 걸리는 게 문제였다.
시도는 좋았지만, 보다 최적화할 수 있는 방법이 필요했고 풀이를 참고했다.

정답 풀이

볼 수 있는 건물의 개수는 생각보다 허무할 정도로 쉽게 구하는 방법이 있었다.

단조 스택의 특성상, 스택의 위쪽에 있는 건물일수록 높이가 낮고, 아래쪽에 있는 건물일수록 높이가 높다. 즉 정렬이 되어 있다.
그러니 현재 건물을 스택에 push하기 직전에는, 현재까지 지나온 건물들 중 자신보다 높은 건물들이 순서대로 쌓여 있는 상태일 것이다.
그러니까 현재 건물을 push하기 전 스택의 크기가 현재까지 지나온 건물들 중 볼 수 있는 건물들의 총 개수가 되는 것이다.
그리고 그 중에서도 스택의 맨 위에 있는 건물이 현재 건물에서 볼 수 있는 건물 중 가장 가까운 건물일 것이다.

한 마디로, 그냥 양방향 순회 총 2번이면 모든 결과를 구할 수가 있었다.
즉 시간 복잡도가 $O(N)$이다.

왼쪽에서 오른쪽으로 순회하면 오른쪽 방향으로만 본다고 생각했지, 이미 지나온 반대 방향의 건물 정보를 알 수 있을 거라고 생각을 못한 것 같다.

import java.io.*;
import java.util.*;

class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        StringBuilder sb = new StringBuilder();
        int[] heights = new int[N + 1];
        int[] rightClosest = new int[N + 1];
        int[] leftClosest = new int[N + 1];
        int[] counts = new int[N + 1];
        String[] input = br.readLine().split(" ");
        
        for (int i = 1; i <= N; i++) {
            heights[i] = Integer.parseInt(input[i - 1]);
        }

        Stack<Integer> stack = new Stack<>();
        for (int i = 1; i <= N; i++) {
            while (!stack.isEmpty() && heights[stack.peek()] <= heights[i]) {
                stack.pop();
            }
            counts[i] = stack.size();
            if (!stack.isEmpty()) {
                leftClosest[i] = stack.peek();
            }
            stack.push(i);
        }

        stack.clear();
        for (int i = N; i > 0; i--) {
            while (!stack.isEmpty() && heights[stack.peek()] <= heights[i]) {
                stack.pop();
            }
            counts[i] += stack.size();
            if (!stack.isEmpty()) {
                rightClosest[i] = stack.peek();
            }
            stack.push(i);
        }

        for (int i = 1; i <= N; i++) {
            if (counts[i] == 0) {
                sb.append(0);
            } else if (leftClosest[i] == 0) {
                sb.append(counts[i]).append(' ').append(rightClosest[i]);
            } else if (rightClosest[i] == 0) {
                sb.append(counts[i]).append(' ').append(leftClosest[i]);
            } else if (rightClosest[i] - i < i - leftClosest[i]) {
                sb.append(counts[i]).append(' ').append(rightClosest[i]);
            } else {
                sb.append(counts[i]).append(' ').append(leftClosest[i]);
            }
            sb.append('\n');
        }

        System.out.print(sb.toString());
    }
}

---

단조 스택을 조금 더 이해하는 계기가 된 것 같다.