문제

https://www.acmicpc.net/problem/2668
세로 두 줄, 가로로 N개의 칸으로 이루어진 표가 있다. 첫째 줄의 각 칸에는 정수 1, 2, …, N이 차례대로 들어 있고 둘째 줄의 각 칸에는 1이상 N이하인 정수가 들어 있다. 첫째 줄에서 숫자를 적절히 뽑으면, 그 뽑힌 정수들이 이루는 집합과, 뽑힌 정수들의 바로 밑의 둘째 줄에 들어있는 정수들이 이루는 집합이 일치한다. 이러한 조건을 만족시키도록 정수들을 뽑되, 최대로 많이 뽑는 방법을 찾는 프로그램을 작성하시오. 예를 들어, N=7인 경우 아래와 같이 표가 주어졌다고 하자.

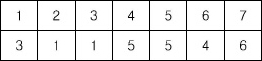
이 경우에는 첫째 줄에서 1, 3, 5를 뽑는 것이 답이다. 첫째 줄의 1, 3, 5밑에는 각각 3, 1, 5가 있으며 두 집합은 일치한다. 이때 집합의 크기는 3이다. 만약 첫째 줄에서 1과 3을 뽑으면, 이들 바로 밑에는 정수 3과 1이 있으므로 두 집합이 일치한다. 그러나, 이 경우에 뽑힌 정수의 개수는 최대가 아니므로 답이 될 수 없다.

입력
첫째 줄에는 N(1≤N≤100)을 나타내는 정수 하나가 주어진다. 그 다음 줄부터는 표의 둘째 줄에 들어가는 정수들이 순서대로 한 줄에 하나씩 입력된다.

출력
첫째 줄에 뽑힌 정수들의 개수를 출력하고, 그 다음 줄부터는 뽑힌 정수들을 작은 수부터 큰 수의 순서로 한 줄에 하나씩 출력한다.

예제 입력 1
7
3
1
1
5
5
4
6

예제 출력 1
3
1
3
5

접근

그렇게까지 어려운 문제가 아닌 것 같은데 내가 너무 접근을 난해하게 한 건지.. 계속 안 풀려서 엄청 애먹었다.
재귀 호출을 해야 된다는 건 알겠는데 구현을 못해내겠더라...

첫째 줄에서 a라는 수를 골랐으면 둘째 줄에서 a 바로 밑에 있는 수도 골라야 한다. 그 수를 b라고 하면 또 첫째 줄에서도 b를 골라야 하고... 이런 식으로 두 줄을 교차해 가며 재귀 호출을 했다.
더 나은 풀이가 있을 것 같아서 조만간 찾아봐야 할 듯...

구현

import java.io.*;
import java.util.*;
import java.util.stream.Collectors;

class Main {
    static int[] table;
    static int[] isSelected;
    static Set<Integer>[] reversed;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        table = new int[N + 1];
        isSelected = new int[N + 1];
        reversed = new Set[N + 1];
        for (int i = 1; i <= N; i++) {
            reversed[i] = new HashSet<>();
        } 
        for (int i = 1; i <= N; i++) {
            table[i] = Integer.parseInt(br.readLine());
            reversed[table[i]].add(i);
        }

        Set<Integer> answer = new HashSet<>();
        for (int i = 1; i <= N; i++) {
            if (dfs(i, new HashSet<>(), true)) {
                answer.add(i);
            }
        }
        
        StringBuilder sb = new StringBuilder();
        sb.append(answer.size()).append("\n");
        for (int num : answer.stream().sorted().collect(Collectors.toList())) {
            sb.append(num).append("\n");
        }
        System.out.print(sb.toString());
    }
    
    private static boolean dfs(int idx, Set<Integer> path, boolean isUpper) {
        if (isUpper) {
            if (isSelected[idx] == 1) {
                return true;
            }
            if (isSelected[idx] == -1) {
                return false;
            }
            if (reversed[idx].isEmpty()) {
                isSelected[idx] = -1;
                return false;
            }

            path.add(idx);
            Set<Integer> tempSet;
            boolean flag = false;
            for (int e : reversed[idx]) {
                tempSet = new HashSet<>(path);
                if (path.contains(e) || dfs(e, tempSet, true)) {
                    flag = true;
                    path.addAll(tempSet);
                }
            }

            if (flag && (path.contains(table[idx]) || dfs(idx, path, false))) {
                for (int e : path) {
                    isSelected[e] = 1;
                }
                return true;
            }
            isSelected[idx] = -1;
            return false;
        }

        if (isSelected[table[idx]] == 1) {
            return true;
        }
        if (isSelected[table[idx]] == -1) {
            return false;
        }

        path.add(table[idx]);
        if (path.contains(table[table[idx]]) || dfs(table[table[idx]], path, true)) {
            if (path.contains(idx) || dfs(idx, path, true)) {
                for (int e : path) {
                    isSelected[e] = 1;
                }
                return true;
            }
        }
        return false;
    }
}