트리(Tree)

References

아래 링크의 강의 중 Section 25. Building a Tree의 내용을 추려 이번 글을 작성하였습니다.
The Coding Interview Bootcamp: Algorithms + Data Structures on Udemy

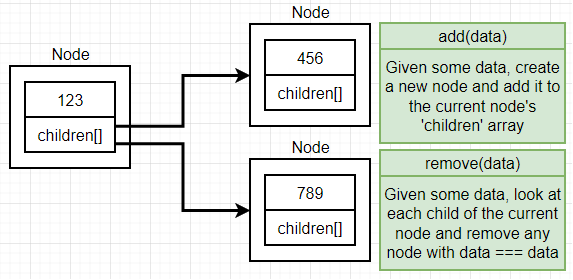
Node

class Node {
  constructor(data) {
    this.data = data;
    this.children = [];
  }
  // node의 입력값 data를 배열로 children에 push
  add(data) {
    const node = new Node(data);
    this.children.push(node);
  }
 // filter() method로써 특정값을 제외한 배열을 반환
  remove(data) {   
    this.children = this.children.filter((node) => {
      return node.data !== data;
    });
  }
}

Tree

class Tree {
  constructor() {
    this.root = null;
  }

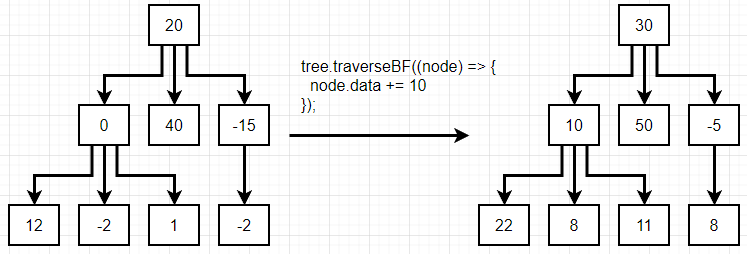
  traverseBF(fn) {
    const arr = [this.root];
    while (arr.length) {
      const node = arr.shift();
      // 그냥 node.children을 push하면 array로 들어가서 nested array 되기 때문에 하나씩 꺼내어 push
      arr.push(...node.children);
      //   for (let child of node.children) {
      //     arr.push(child);
      //   }
      fn(node);
    }
  }

  traverseDF(fn) {
    const arr = [this.root];
    while (arr.length) {
      const node = arr.shift();

      arr.unshift(...node.children);
      fn(node);
    }
  }
}

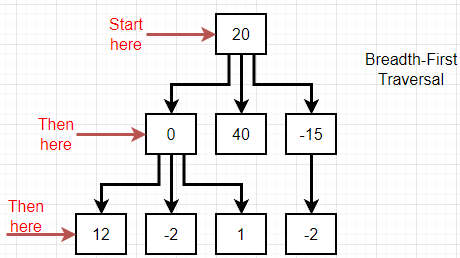
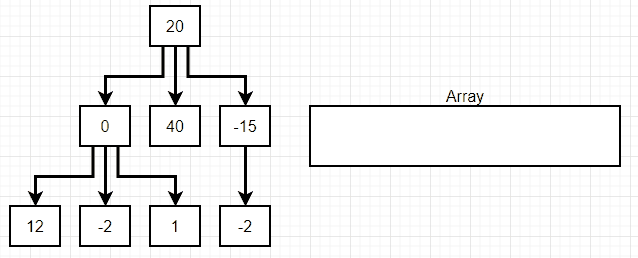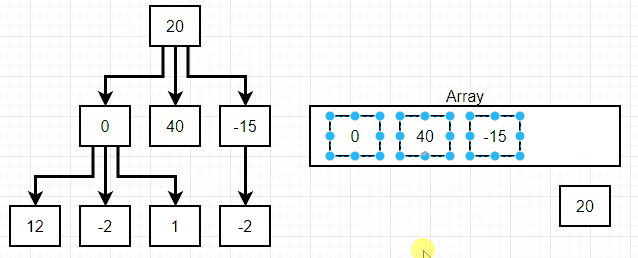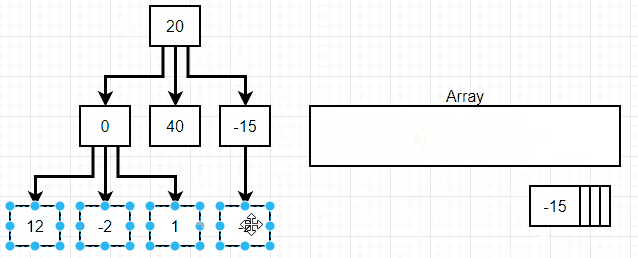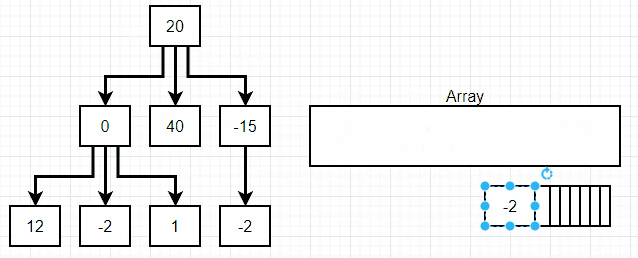
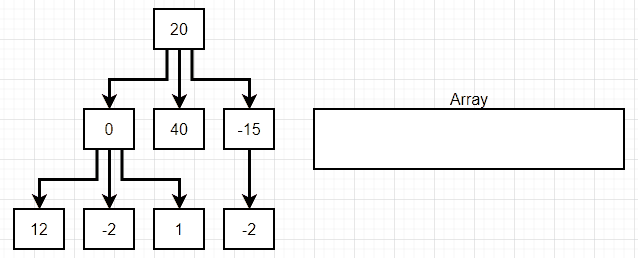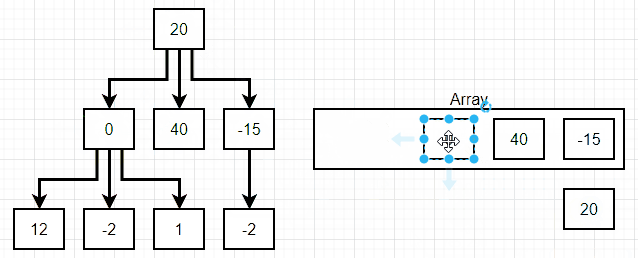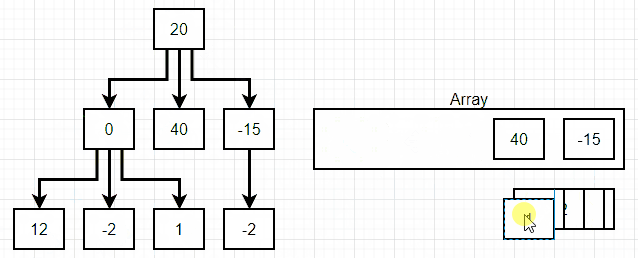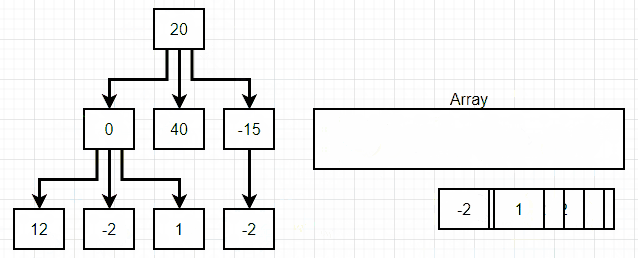
너비 탐색(breadth first search)

위 그림에서 볼 수 있듯 너비 탐색(breadth first search)에서는 linked list의 맨 상위 단계에서 맨 하위 단계로 내려가면서, 각 단계별 첫 값에서 끝 값까지를 탐색한다.

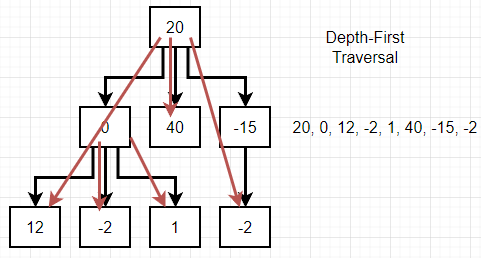
깊이 탐색(depth first search)

위 그림에서 볼 수 있듯 깊이 탐색(depth first search)의 경우 linked list의 맨 상위 단계에서 맨 하위 단계로 내려가면서 각 단계의 맨 첫 값에 하위값이 있다면 그 하위값들부터 우선 탐색을 하고, 다시 상위 단계로 돌아와 하위값들을 탐색하는 과정을 반복한다.

Entire Code

class Node {
  constructor(data) {
    this.data = data;
    this.children = [];
  }
  
  add(data) {
    const node = new Node(data);
    this.children.push(node);
  }

  remove(data) {
    this.children = this.children.filter((node) => {
      return node.data !== data;
    });
  }
}

class Tree {
  constructor() {
    this.root = null;
  }

  traverseBF(fn) {
    const arr = [this.root];
    while (arr.length) {
      const node = arr.shift();
      
      arr.push(...node.children);
      //   for (let child of node.children) {
      //     arr.push(child);
      //   }
      fn(node);
    }
  }

  traverseDF(fn) {
    const arr = [this.root];
    while (arr.length) {
      const node = arr.shift();

      arr.unshift(...node.children);
      fn(node);
    }
  }
}