백준 / 2565 / 전깃줄 / java

package backjun.H동적계획;

import java.util.Scanner;
import java.util.Arrays;

public class 전깃줄 {
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);

        int n = sc.nextInt();
        int[][] arr = new int[n][2];
        int[] dp = new int[n];

        for(int i=0; i<n; i++){
            int a = sc.nextInt(), b= sc.nextInt();
            arr[i][0] = a; arr[i][1] = b;
            dp[i] = 1;
        }
        sc.close();

        Arrays.sort(arr, (o1, o2) -> { return o1[1] - o2[1];});

        for(int i=0; i<n; i++){
            for(int j=i; j<n; j++){
                if(arr[j][0] > arr[i][0]){
                    dp[j] = Math.max(dp[j], dp[i]+1);
                }
            }
        }
        // Arrays.stream(dp).forEach(a->{System.out.print(a + " ");});
        System.out.println(n - Arrays.stream(dp).max().getAsInt());
    }
}

LIS(Longest Increasing Subsequence) - 최장 증가 부분 수열 알고리즘 응용 문제

우선 입력 받은 전깃줄을 a전봇대 혹은 b 전봇대를 기준으로 정렬한다.

a 전봇대를 기준으로 정렬했다면 LIS를 b 전봇대에서 구하면 되고
b 전봇대를 기준으로 정렬했다면 LIS를 a 전봇대에서 구하면 된다.

구한 LIS에를 n에서 뺌으로서 정답을 구할 수 있다.

이런 방식이 가능한 이유를 생각해보자

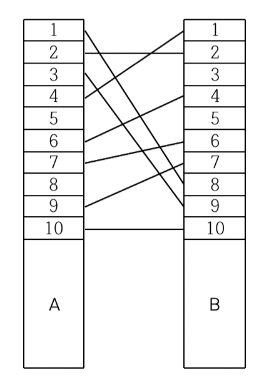
이 그림은 예제로 주어진 예제 입력에 대해 a 전봇대 기준으로 정렬한 그림이다. 이 그림에서 B 전봇대로 LIS를 생각해보면 1, 4, 6, 7, 10 혹은 2, 4, 6, 7, 10이다

이것을 다르게 생각해보면 LIS 1, 4, 6, 7, 10으로 생각했을 때 B 전봇대에서 전깃줄 2, 8, 9만 없으면 교차하지 않은 전깃줄을 만들 수 있다.

이렇기 때문에 LIS를 n에서 뺌으로서 정답을 구할 수 있는것이다.

---

정렬을 위해 처음으로 Java의 람다를 사용해봤다.

위 코드에서 일차원 배열 정렬과 비교 해보자

# 1차원 배열의 정렬
Arrays.sort(arr)

# 2차원 배열의 정렬
Arrays.sort(arr, (o1, o2) -> { return o1[1] - o2[1];});

-> 지금은 우선 사용법만 익히고 해당 코드의 의미는 다른 포스팅에서 쭉 살펴본다.