1. 선형 탐색 알고리즘(Linear Search Algorith)
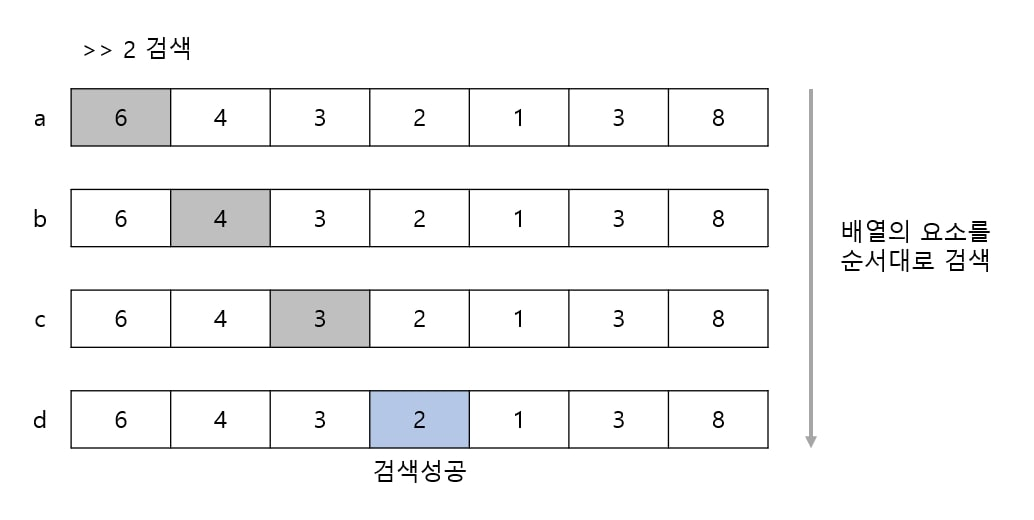
맨 앞 부터 순서대로 요소를 검색하는 알고리즘
1. 맨 끝부터 하나하나 원하는 값을 찾아본다.
2. 원하는 값을 찾으면 탐색을 종료한다.
a. 인덱스가 0인 요소 6을 선택, 검색하려는 값이 아닙니다.
b. 인덱스가 1인 요소 4을 선택, 검색하려는 값이 아닙니다.
c. 인덱스가 2인 요소 3을 선택, 검색하려는 값이 아닙니다.
d. 인덱스가 3인 요소 2을 선택, 검색하려는 값입니다. 검색 성공!
class LinearSearchAlg{
static int LinearSearchAlg(int[] a, int n, int key) {
int i = 0;
while(true) {
if(i==n)
return -1;
if(a[i] == key)
return i;
i++;
}
}
public static void main(String[] args){
Scanner stdIn = new Scanner(System.in);
System.out.print("요솟수 : ");
int num = stdIn.nextInt();
int[] x = new int[num];
for(int i = 0; i < num; i++){
System.out.print("x[" + i + "]: ");
x[i] = stdIn.nextInt();
}
System.out.print("검색할 값:");
int ky = stdIn.nextInt();
int idx = seqSearch(x, num, ky);
if(idx == -1)
System.out.println("그 값의 요소가 없습니다.");
else
System.out.println?("그 값은 x[" + idx + "]에 있습니다.");
}
}실행결과
요솟수: 7
x[0]: 6
x[1]: 4
x[2]: 3
x[3]: 2
x[4]: 1
x[5]: 2
x[6]: 8
검색할 값 : 2
그 값은 x[3]에 있습니다.시간 복잡도
static int LinearSearchAlg(int[] a, int n, int key) {
① int 1 = 0;
② while(i<n) {
③ if(a[i] == key)
④ return i;
⑤ i++;
}
⑥ return -1;
}| 단계 | 실행 횟수 | 복잡도 |
|---|---|---|
| ① | 1 | O(1) |
| ② | n/2 | O(n) |
| ③ | n/2 | O(n) |
| ④ | 1 | O(1) |
| ⑤ | n/2 | O(n) |
| ⑥ | 1 | O(1) |
2. 이진 탐색 알고리즘(Binary Search Algorith)
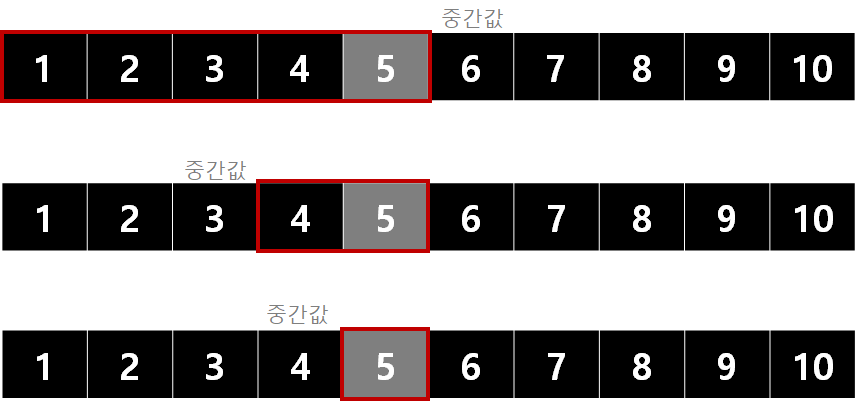
중간지점을 기준으로 데이터를 반씩 나눠서 탐색하는 알고리즘
1. 중간지점을 선택한 뒤, 중간지점을 기준으로 왼쪽 혹은 오른쪽 부분만 남긴다.
2. 남긴 부분 중에서 다시 중간지점을 선택한 뒤, 왼쪽 혹은 오른쪽만 남긴다.
3. 위 과정을 원하는 값을 찾을 때 까지 반복한다.
class BinSearch{
static int binSearch(int[] a, int n, int key){
int pl = 0;
int pr = n-1;
do{
int pc = (pl+pr) / 2;
if(a[pc] == key)
return pc;
else if(a[pc] < key)
pr = pc - 1;
} while(pl <= pr);
return -1;
}
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
Sytstem.out.print("요솟수: ");
int num = stdIn.nextInt();
int[] x = new int[num];
System.out.println("오름차순으로 입력하세요.");
System.out.print("x[0]: ");
x[0] = stdIn.nextInt();
for(int i = 0; i < num; i++){
do{
System.out.print("x["+ i +"]:");
x[i] = stdIn.nextInt();
}while(x[i] < x[i-1];
}
System.out.print("검색할 값: ");
int ky = stdIn.nextInt();
int idx = binSearch(x, num, ky);
if(idx == -1)
System.out.println("그 값의 요소가 없습니다.");
else
System.out.println("그 값은 x["+idx+"]에 있습니다.");
}
}
실행 결과
요솟수: 7
오름차순으로 입력하세요.
x[0]: 15
x[1]: 27
x[2]: 39
x[3]: 77
x[4]: 92
x[5]: 108
x[6]: 121
검색할 값: 39
그 값은 x[2]에 있습니다.시간 복잡도
static int binSearch(int[] a, int n, int key){
① int pl = 0;
② int pr = n -1;
do{
③ int pc = (pl+pr)/2;
④ if(a[pc] == key)
⑤ return pc;
⑥ else if(a[pc] < key)
⑦ pl = pc + 1;
else
⑧ pr = pc - 1;
⑨ } while(pl <= pr);
⑩ return -1;
}| 단계 | 실행 횟수 | 복잡도 |
|---|---|---|
| ① | 1 | O(1) |
| ② | log n | O(log n) |
| ③ | log n | O(log n) |
| ④ | 1 | O(1) |
| ⑤ | log n | O(log n) |
| ⑥ | log n | O(log n) |
| ⑦ | log n | O(log n) |
| ⑧ | log n | O(log n) |
| ⑨ | log n | O(log n) |
| ⑩ | 1 | O(1) |
3. 해시 탐색 알고리즘(Hash Search Algoritm)
값과 index를 미리 연결해 둠으로써 짧은 시간에 탐색할 수 있는 알고리즘
함수를 사용하여 데이터를 보관 후 사용된 함수를 사용하여 한 번에 데이터를 탐색
아이디어
1차 아이디어
처음에는 데이터와 같은 index에 저장
최소한 데이터의 종류 만큼의 index 필요
2차 아이디어
데이터에 함수(일정 계산)을 적용하여 나온 값을 index로 하여 보관하는 방법
해시 함수 : 어떤 값이 주어졌을 때, 그 값을 대표하는 값을 계산하는 함수
해시 값 : 해시 함수의 계산으로 나온 값
4. 이진 탐색 트리(BST/ Binary Search Tree)
트리 자료구조를 이용한 탐색 트리
왼쪽 서브트리의 키값들은 root의 키값보다 작다.
오른쪽 서브트리의 키값들은 root의 키값보다 크다.
왼쪽, 오른쪽 서브트리들을 각각 모두 BST 정의를 만족한다.
BST의 모든 node들의 키값은 unique
4가지를 모두 만족해야 한다.
탐색 알고리즘
어떠한 BST에서 원하는 값을 찾고자 할 때, root 값을 기준으로
- 원하는 값 > root 키 값 : 오른쪽 서브트리로 이동
- 원하는 값 < root 키 값 : 왼쪽 서브트리로 이동
- 원하는 값 = root 키 값 : 탐색 종료
삽입 알고리즘
어떠한 값을 삽입하고자 할 때
1. 탐색 알고리즘을 먼저 수행
2. 탐색 실패 시, 탐색이 종료된 위치에 해당 노드를 삽입
3. 탐색 성공 시, 이미 저장되어있는 키값이므로 삽입에 실패
삭제 알고리즘
어떠한 값을 삭제하고자 할 때,
1. 위의 탐색 알고리즘을 먼저 수행
2. 삭제하려는 노드의 차수에 따라
- 차수 : 0(leaf node) - 그냥 삭제
- 차수 : 1(한 개의 자식 존재) : 삭제하고 자식을 삭제한 자리에 붙인다.
- 차수 : 2(자신의 대체할 노드를 찾는다) :
삭제할 노드의 왼쪽 서브트리에서 가장 큰 값
오른쪽 서브트리에서 가장 작은 값
을 대체할 노드로 정한다.
Reference
https://bba-dda.tistory.com/21
https://product.kyobobook.co.kr/detail/S000001817897