#55. Jump Game

Jump Game

You are given an integer array nums. You are initially positioned at the array's first index, and each element in the array represents your maximum jump length at that position.

Return true if you can reach the last index, or false otherwise.

 

Example 1:

Input: nums = [2,3,1,1,4]
Output: true
Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.
Example 2:

Input: nums = [3,2,1,0,4]
Output: false
Explanation: You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
 

Constraints:

1 <= nums.length <= 10^4
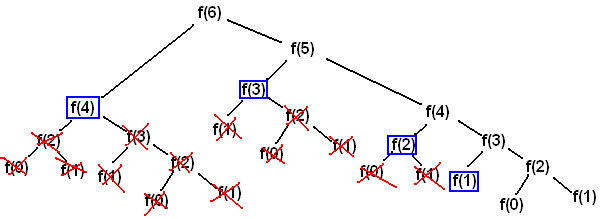
0 <= nums[i] <= 10^5

1st Try : brute force --> FAIL

class Solution {
public:
    bool canJump(vector<int>& nums) {
        if(nums.size() == 1) return true;
        int fst_val = *(nums.begin());
        for(int ix = 1; ix <= fst_val; ix++)
        {
            vector<int> copy_nums(nums.begin()+ix, nums.end());
            if(canJump(copy_nums)) return true;
        }
        return false;
    }

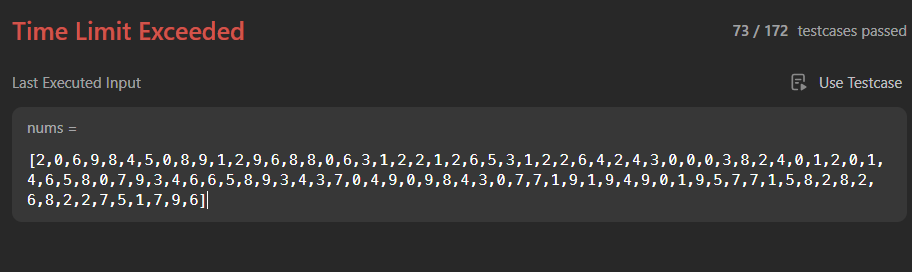
Unfortunately, only 73 cases work out and it gives me the time-out error. I forgot to keep in mind of meeting time complexity, which is O(N^M) in this case.

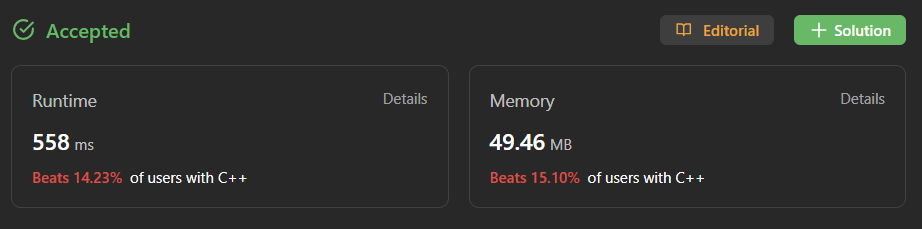
2nd Try : dynamic programming --> SUCCESS

class Solution {
public:
    int cache[10000];
    bool canJump(vector<int>& nums) {
        fill(begin(cache), end(cache), -1); 
        return canJump2(nums, 0);
    }
    int canJump2(vector<int>& nums, int idx)
    {
        if(cache[idx] == 1 || cache[idx] == 0) return cache[idx];
        if(idx > nums.size()) return 0;
        if(idx == nums.size()-1) return 1;
        for(int i = 1; i <= nums[idx]; i++)
        {
            if(canJump2(nums, idx+i) == 1)
            {
                cache[idx] = 1;
                return 1;
            }
        }
        cache[idx] = 0;
        return 0;
    }
};

I tried to optimize my first solution and it worked,but it gives me a disappointing result as you can see. The runtime takes more than 500ms and I guess if there was a tricky test case, then the solution might not work though. Anyway, the most important thing to be considered using dynamic programming in this case was in this part of the source code.

		for{...recursively function call...}
        cache[idx] = 0;
        return 0;

I initialized the cache memory array by -1 because of considering both success case(1) and fail cases(0). When we got to the end point, which is the success case, the functions called will return recursively. It means when we found out the way to go to the end point, then the program will be finished. For optimization, I marked the index as fail confirmation after looping all the possible cases, which means impossible to reach to the end point. Caching fail cases like above prevents the program from inefficiently calling the same functions.

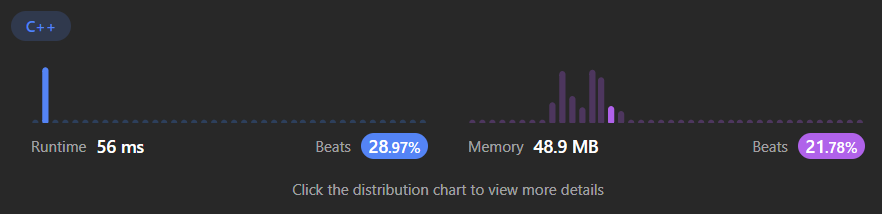
Most voted solution

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int size = nums.size();
        int i, reach = 0; 
        for(i = 0; i < size && i <= reach; i++)
        {
            reach = max(reach, i+nums[i]);
        }
        return i == size;
    }
};

This solution is very intuitive because it starts from the front, not backwards. And it starts from the simple fact that we can jump on certain element from 1 to numbers of the element. So, if there is a way to go to the end point of the array, then the before element should make possible for reaching there and it applies the same as for the element recursively. So, all we need to do is looping through the array and expanding the reachable point as possible. Reach point itself guarantees that every elements should be reachable before the element.