#169. Boyer-Moore Major Voting Algorithm

Majority Element

Given an array nums of size n, return the majority element.

The majority element is the element that appears more than ⌊n / 2⌋ times. You may assume that the majority element always exists in the array.

 

Example 1:

Input: nums = [3,2,3]
Output: 3
Example 2:

Input: nums = [2,2,1,1,1,2,2]
Output: 2
 

Constraints:

n == nums.length
1 <= n <= 5 * 10^4
-109 <= nums[i] <= 10^9

1st Try --> SUCCESS

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        return nums[nums.size()/2];
    }
}; 

This solution is the first one that comes up through my mind and it is very intuitive and easy-to-understand solution. However, the array should be sorted and the time complexity should be O(NlogN).

Boyer-Moore Voting Algorithm

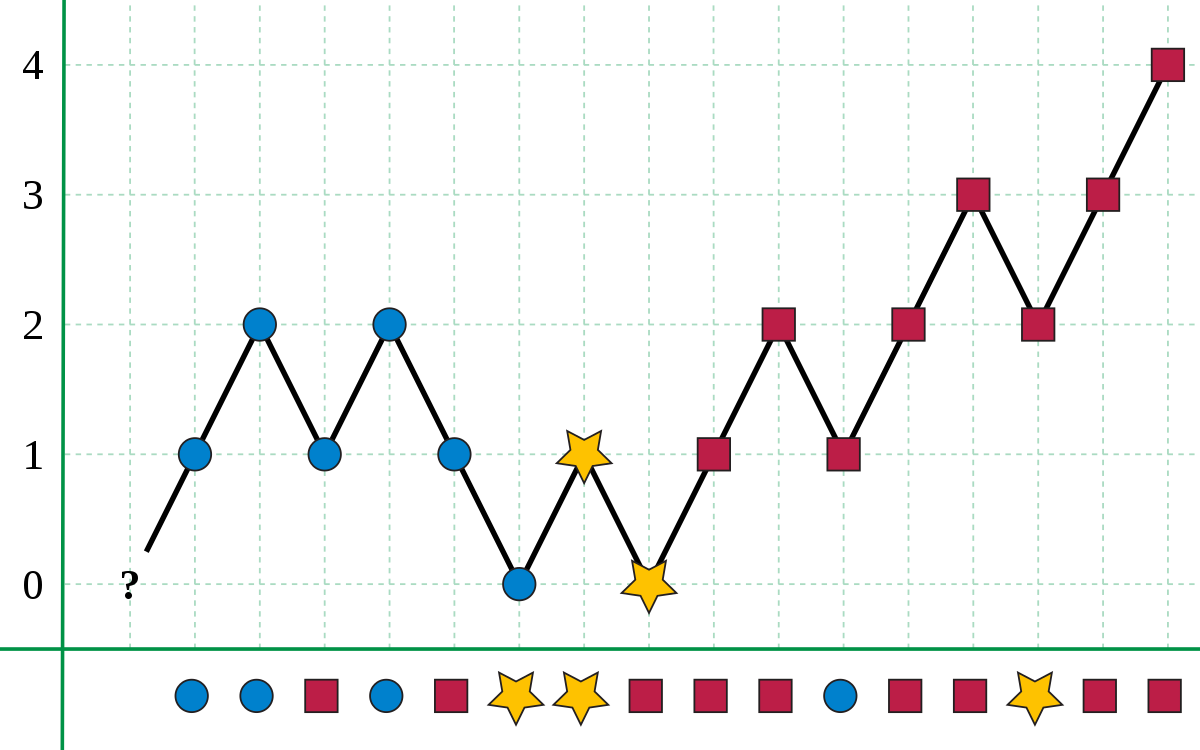
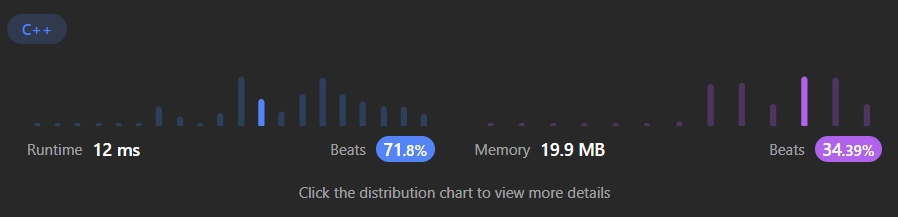
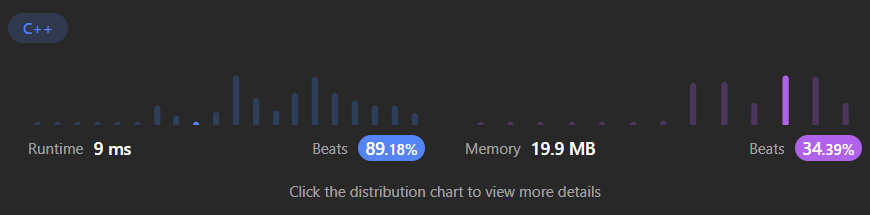
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int n = nums.size();
        int candidate;
        int votes = 0;
        for( auto e : nums )
        {
            // Finding Majority Candidate
            // This doesn't enough for guaranteeing that the candidate 
            // has more votes than half of the total in general case 
            // except for this problem because this problem guarantees 
            // that there is a majority candidate.
            if( votes == 0 )
            {
                candidate = e;
            }
            if( candidate == e )
            {
                votes++;
            }
            else
            {
                votes--;
            }
        }
        // Checking Majority Candidate by another traversal.
        int count = 0;
        for( auto e : nums )
        {
            if( candidate == e ) count++;
        }
        if( count > n/2 )
            return candidate;
        else 
            return -1;
        return candidate;
    }
};

when skip the checking Majority Candidate by another traversal

when include the checking Majority Candidate by another traversal

taking exactly 2 times than skip version.

This solution starts from the suppose that there should be a majority candidate. So, without the suppose, this algorithm should be fail. For understanding this algorithm intuitively, we can consider 2 points by thinking experiment.

1. line up the majority candidate at the front.
   'xxxxxxxabcdef'
   This should be look like above. Supposing there is a majority candidate, discounting votes of every other candidates from the majority candidate should be more than zero.

2. Worst case.
   'xyyxyyxxxyx'
   This should be look like above. It seems very competitive election by the way. We can see this kind of election in reality in occasion by the way. In this case, according to the Boyer-Moore Voting Alogrithm, the majority candidate continues to be changed. However, although the other candidate can take a leading position temporarily, the majority candidate will eventually get the leading position because it always has more votes than the others, so he can kill the others' votes.