기본 알고리즘 이론 (프로그래밍)

Flex·2022년 3월 14일

algorithm

알고리즘 모음

목록 보기

1/3

🧮 알고리즘 복잡도 (시간 복잡도)

입력 크기의 값에 대해 단위 연산을 몇 번 수행하는지 계산하여,
알고리즘의 수행시간을 평가하는 방법입니다.

아래와 같이 3가지 점근적 표현법이 있습니다.
1. 빅오 표기법 : 최악의 상황을 고려하여 성능 측정 결과 표현
2. 세타 표기법 : 평균적인 경우에서의 성능 측정 결과 표현
3. 오메가 표기법 : 최선의 상황일 때의 성능 측정 결과 표현

일반적으로 빅오(O) 표기법이 가장 많이 쓰입니다.

1. 알고리즘 평가 지표

알고리즘 성능 평가 지표 : 정확성, 작업량, 메모리 사용량, 최적성, 효율성(시간 복잡도 / 공간 복잡도)

많은 알고리즘 해결문제에서 메모리 사용량은 큰 제한을 두지 않습니다.
따라서 효율성 측면에서는 시간 복잡도가 가장 중요하다고 할 수 있습니다.

2. 시간 복잡도

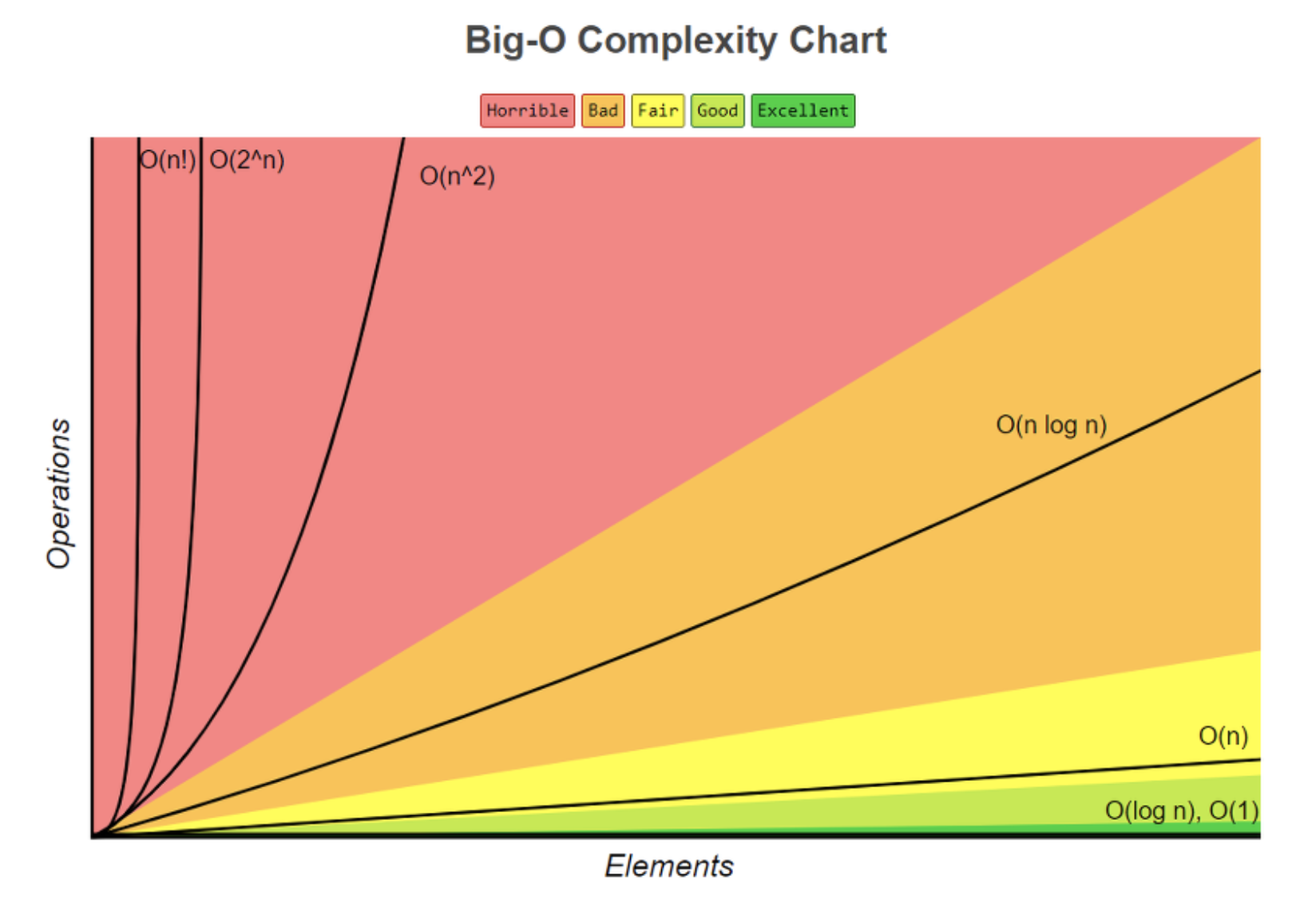
빅오(O) 표기법에 따른 시간 복잡도는 아래 차트와 같습니다.
아래쪽에 위치한 표기법일수록 요소가 늘어나도 시간에 큰 영향을 주지 않습니다.

3. 빅오(O) 표기법

반복문의 생김새에 따라 시간 복잡도가 달라지게 됩니다.

Example 1

function big_o(n) {
  let sum = 0; // 1회
  sum = n * 2; // 1회
  return sum; // 1회
}

위 예제는 각각 1회로써, 총 3회의 코드가 실행됩니다.
3 --> O(1) 으로 표시됩니다.

Example 2

function big_o(arr, n) {
  let sum = 0; // 1회
  
  for (let i = 0; i < n; i++) { // n회
    sum += arr[i];
  }
  
  return sum; // 1회
}

위 예제는 for문이 하나 있어 n회 실행하는 라인이 포함됩니다.
따라서 n + 2 --> O(N) 으로 표시됩니다.

Example 3

function big_o(arr, n) {
  let sum = 0; // 1회
  
  for (let i = 0; i < n; i++) { // n * n = n^2회
    for (let j = 0; j < n; j++) {
      sum += arr[i];
    }
  }
  
  return sum; // 1회

위 예제는 2중 for문을 사용하여 n * n 회 실행됩니다.
따라서 n2 + 2 --> O(N2) 으로 표시됩니다.
❗️ 시간복잡도의 엄청난 증가로 인해 2중 반복문은 사용하지 않는것이 바람직합니다.

Example 4

function big_o(arr, n) {
  let sum = 0; // 1회
  
  for (let i = 0; i < n; i *= 2) { // n/2 회
    sum += arr[i];
  }
  
  return sum; // 1회

위 예제는 for문의 i가 두배씩 증가하며 실행됩니다.
따라서 n/2 + 2 --> O(logN) 으로 표시됩니다.

🧮 경우의 수

어떤 사건 혹은 일이 일어날 수 있는 경우의 가짓수를 수로 표현합니다.

일상 생활에서의 경우의 수는 다음 예시들과 같습니다.
- 주사위 : 던지는 결과, 1~6 사이의 숫자이므로 경우의 수는 6
- 동전 : 던지는 결과, 앞 혹은 뒷면이므로 경우의 수는 2
- 가위바위보 : 가위, 바위, 보 중 하나를 낼 수 있으므로 경우의 수는 3
- 윷 : 도, 개, 걸, 윷, 모 중 하나이므로 경우의 수는 5
  ...
완전탐색으로 경우의 수를 푸는 알고리즘은 아래와 같습니다.
- 순열 : 서로 다른 n개의 원소 중에서 r을 중복없이 골라 순서에 상관 있게 나열하는 경우의 수
  (n P r)
- 조합 : 서로 다른 n개의 원소 중에서 r을 중복없이 골라 순서에 상관 없이 나열하는 경우의 수
  (n C r)
- 중복 순열 : 서로 다른 n개의 원소 중에서 r개를 중복 있게 골라 순서에 상관 있게 나열하는 경우의 수 (n H)

1. 순열 (Permutaion)

서로 다른 n개의 원소 중에서 r을 중복없이 골라 순서에 상관 있게 나열하는 경우의 수입니다.

3개의 알파벳(A, B, C)으로 단어를 만드는 경우의 수에 대한 예제 링크는 하단에 있습니다.

🔖 for문 중첩 예제
🔖 재귀함수 예제

2. 조합 (combination)

서로 다른 n개의 원소 중에서 r을 중복없이 골라 순서에 상관 없이 나열하는 경우의 수입니다.

4개의 숫자 카드에서 2개를 뽑는 경우의 수에 대한 예제 링크는 하단에 있습니다.

🔖 for문 중첩 예제
🔖 재귀함수 예제

🧮 점화식

점화식(재귀식) 이란?
수열에서 이웃하는 두 개의 항 사이에 성립하는 관계를 나타낸 관계식입니다.

대표적인 점화식은 아래와 같습니다.
- 등차 수열 : F(n) = F(n-1) + a
- 등비 수열 : F(n) = F(n-1) * a
- 팩토리얼 : F(n) = F(n-1) * n
- 피보나치 수열 : F(n) = F(n-1) + F(n-2)

프로그래밍으로는 재귀함수로 표현할 수 있습니다.
추후 Recursive, Dynamic 프로그래밍에 쓰일 수 있습니다.

재귀함수 구현시 고려할 점

Stop 조건

반복할 부분

✅ 두 개만 완벽하게 구분할 수 있다면 재귀함수로 쉽게 변환시킬 수 있습니다.

💵 오늘을 살자

다음 포스트