머신러닝, 딥러닝에 필요한 기초 수학 - 편미분

TS2·2021년 7월 22일
도함수로지스틱 시그모이드미분소프트맥스야코비안편미분
0

기초 수학 with 파이썬

목록 보기
5/7

1. 편미분의 정의

일변수 스칼라함수에서 이제, 다변수 함수로 확장한다.

다변수 함수에서 순간변화율(평균변화율의 극한값)을 정의할 때 문제가 생긴다. 예로 이변수 함수의 특정 점을 기준으로 변화율을 계산할 때, 어느 방향으로 움직였느냐에 따라 평균변화율이 달라진다. 이래서는 순간변화율을 정의할 수 없다.

그러나, 다변수함수 미분시엔 '편미분'을 통해 기존 일변수 스칼라함수 처럼 손쉽게 계산할 수 있게 할 수 있다. 다른 변수는 고정하고 나머지 변수에 대한 순간변화율을 계산하는 것.

아래 주소에서 시각적으로 확인해보자.

https://metamath1.github.io/noviceml/partial.html

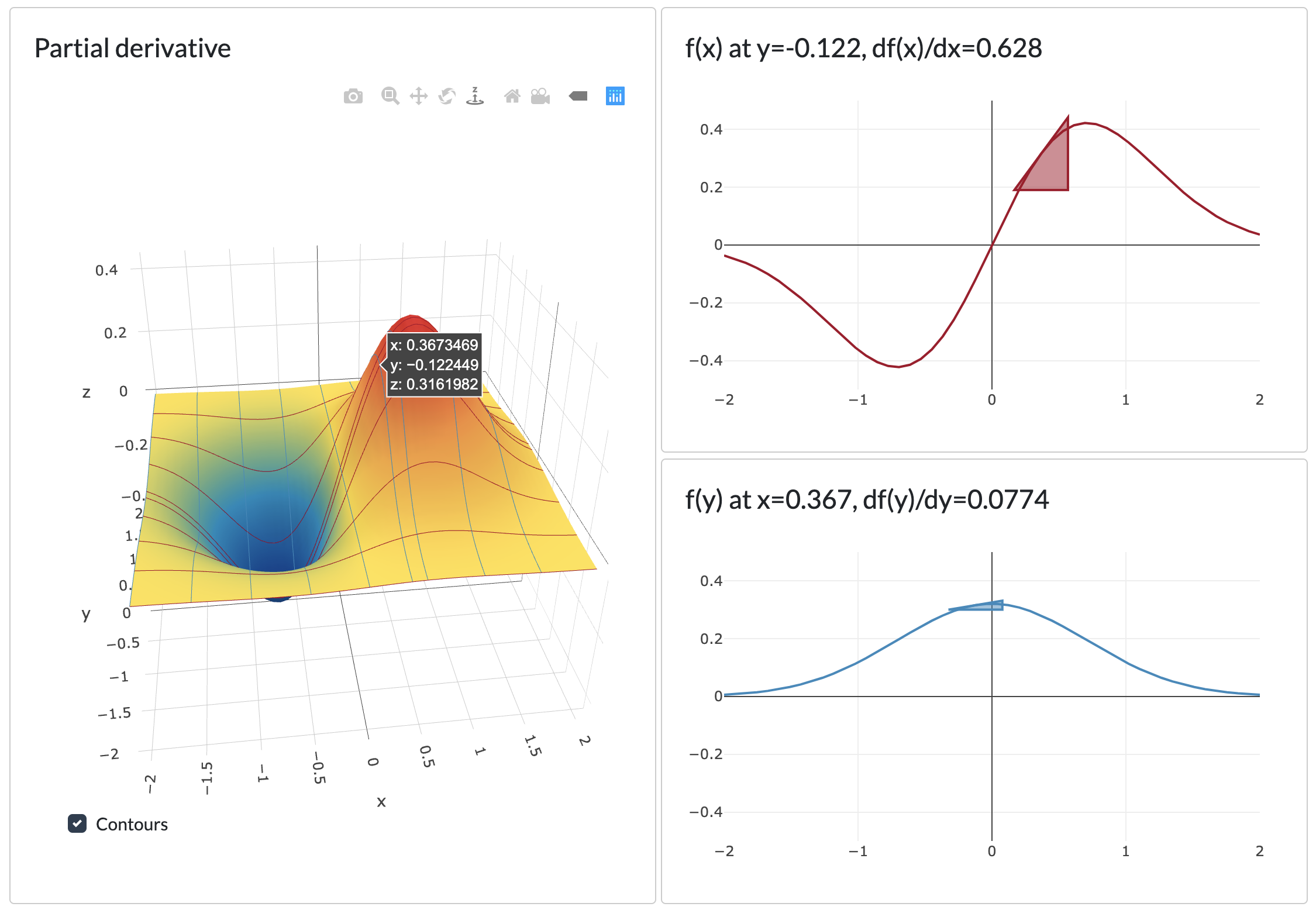
-> y=-0.122에 고정했을 때의 곡선상의 점의 순간변화율 ddx\frac{d}{dx}를 표시해준다.

편미분
다변수 스칼라함수에서 한 변수만 제외한 모든 변수를 고정(상수)시키고 일변수 함수화한 후 미분한다.

  • 다른 변수 (x1,x2,...,xn)(x_1, x_2, ..., x_n)를 상수 취급하고 미분한다.
  • 즉, x\bold x 벡터변수의 각 변수별로 나머지 변수를 상수 취급하고 미분한다.
  • 이때 미분한 결과를 각 변수에 대한 편미분계수라 한다.
∂∂xf(x1,x2,...,xn)=lim⁡h→0f(x1,x2,...,xn)−f(x1,x2,...,xn)h\frac{\partial}{\partial x} f(x_1, x_2, ..., x_n) = \lim\limits_{h \to 0}\frac{f(x_1, x_2, ..., x_n) - f(x_1, x_2, ..., x_n)}{h}

  • 벡터변수 x\bold x의 변수 중 k번째 변수로 미분하라는 뜻.

  • 편도함수는 변수(, 벡터)의 개수만큼 계산할 수 있다.

    (1) 편미분 예시

    예제)
    z=x2+3xy+y−3z=x^2+3xy+y-3에 대해 도함수 ∂z∂x\frac{\partial z}{\partial x}와 ∂z∂y\frac{\partial z}{\partial y}를 구하고, (4, -2)에서 편미분계수를 구하라.

    -> x에 대해 도함수를 구하고, y에 대해 도함수를 구한 후 각 도함수에 (4, -2)를 대입한다.
    ∂z∂x\frac{\partial z}{\partial x} = 2x+3y -> 2
    ∂z∂y\frac{\partial z}{\partial y} = 3x+1 -> 13

    2. 다변수 함수의 연쇄법칙

(1) 입력변수 1, 중간변수 2, 출력변수 1

결국 x→f(x)=y→g(y)=zx \to f(x) = y \to g(y) = z인 경우에 대한 합성함수를 계산하는 것

만일, 입력변수가 tt, 중간변수가 x(t)x(t), y(t)y(t), 출력변수가 zz인 경우
각 함수의 미분 관계는 아래와 같이 표시할 수 있다.

t→dxdt→x(t)t \to \frac{dx}{dt} \to x(t)
t→dydt→y(t)t \to \frac{dy}{dt} \to y(t)
x(t)→∂z∂x→zx(t) \to \frac{\partial z}{\partial x} \to z
y(t)→∂z∂y→zy(t) \to \frac{\partial z}{\partial y} \to z

결국, x에 대한 z의 변화율이므로, 각 합성함수에 해당하는 순간변화율을 곱하고 더하면 된다.

dzdx=∂z∂xdxdt+∂z∂ydydt\frac{dz}{dx} = \frac{\partial z}{\partial x}\frac{dx}{dt} + \frac{\partial z}{\partial y}\frac{dy}{dt}
(2) 입력변수 2, 중간변수 2, 출력변수 1

입력변수가 rr, ss 이고, 중간변수가 x(r,s)x(r,s), y(r,s)y(r,s), 출력변수가 zz인 경우도

r→∂x∂r→x(r,s)r \to \frac{\partial x}{\partial r} \to x(r, s)
r→∂y∂r→y(r,s)r \to \frac{\partial y}{\partial r} \to y(r, s)
x(r,s)→∂z∂x→zx(r, s) \to \frac{\partial z}{\partial x} \to z
y(r,s)→∂z∂y→zy(r, s) \to \frac{\partial z}{\partial y} \to z

s→∂x∂s→x(r,s)s \to \frac{\partial x}{\partial s} \to x(r, s)
s→∂y∂s→y(r,s)s \to \frac{\partial y}{\partial s} \to y(r, s)
x(r,s)→∂z∂x→zx(r, s) \to \frac{\partial z}{\partial x} \to z
y(r,s)→∂z∂y→zy(r, s) \to \frac{\partial z}{\partial y} \to z

케이스가 되므로, 각 입력변수별로 순간변화율을 곱한 후, 더하면 된다.

∂z∂r=∂z∂x∂x∂r+∂z∂y∂y∂r\frac{\partial z}{\partial r} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial r} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial r}
∂z∂s=∂z∂x∂x∂s+∂z∂y∂y∂s\frac{\partial z}{\partial s} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial s} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial s}
(3) 입력변수 2, 출력변수 2 - 야코비안(Jacobian)

편도함수를 블록 형태(행렬)로 작성한 것을 야코비 행렬 또는 야코비안이라 한다.

입력변수가 m=(x,y)m=(x, y), 출력변수 n=(w,z)n=(w, z)로 각 2개씩인 경우, 출력의 순간변화율은 총 4가지 조합이 발생하게 된다.

∂w∂x,∂z∂x,∂w∂y,∂z∂y\frac{\partial w}{\partial x}, \frac{\partial z}{\partial x} , \frac{\partial w}{\partial y}, \frac{\partial z}{\partial y}

일반적으로 F=Rn→Rm\bold F = \reals^n \to \reals^m인 함수에 대해 m∗nm * n개 편도함수를 아래와 같이 표시한다.

[∂f1∂x1∂f1∂x2...∂f1∂xn∂f2∂x1∂f2∂x2...∂f2∂xn............∂fm∂x1∂fm∂x2...∂fm∂xn]\begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & ... & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & ... & \frac{\partial f_2}{\partial x_n} \\ ... & ... & ... & ... \\ \frac{\partial f_m}{\partial x_1} & \frac{\partial f_m}{\partial x_2} & ... & \frac{\partial f_m}{\partial x_n} \\ \end{bmatrix}

행 : 입력(nn개)
열 : 출력(mm개)
이고, 아래로 분자의 첨자가 증가하는 것을 '분자레이아웃'이라 부름

3. 특별한 함수의 미분

(1) 로지스틱 시그모이드 함수

σ(z)=11+e−1\sigma(z) = \frac{1}{1+e^{-1}}

를 미분할 땐, 나눗셈법칙으로 적용하면 되는데, 과정은 다 이해했으므로 결과만 쓴다.

ddzσ(z)=σ(z)(1−σ(z))\frac{d}{dz}\sigma(z) = \sigma(z)(1-\sigma(z))

(2) 소프트맥수 함수

다변수 벡터함수인데, 미분하면 야코비안이 나옴

si(z)=eiz∑k=1Kekzfori=,...,Kandz=(z1,...,zK)∈RKs_i(\bold z) = \frac{e^z_i}{ \sum_{k=1}^K e^z_k} for i = , ..., K and \bold z = (z_1, ..., z_K) \in \reals^K

이 글을 참고하자.
https://ichi.pro/ko/softmax-hamsuwa-beomju-hyeong-gyocha-enteulopi-sonsil-ui-mibun-281264250716625

profile
TS2
샴푸아닙니다. TSE입니다.
이전 포스트

머신러닝, 딥러닝에 필요한 기초 수학 - 미분

다음 포스트

머신러닝, 딥러닝에 필요한 기초 수학 - 수치미분과 자동미분(1)

1개의 댓글

comment-user-thumbnail
최원석
2023년 10월 15일

안녕하세요 글 잘 보고 있어요..!
제가 요즘 많이 고심하는데도 모르겠어서
여쭤보고 싶은 공업수학 문제가 있는데
혹시 답변 해주실 수 있으실까요..?
곤란 하시다면 답변 안 해주셔도 괜찮아요
문제는 이거예요…!

“분리가능 상미분 방정식은 양형태 상미분 방정식의 일부이고, 완전 상미분 방정식은 음형태 상미분 방정식 일부라고 볼 수 있다.
양형태의 상미분 방정식 중 분리가능한 상미분 방정식을 제외하고 남은 상미분 방정식들은 어떤 것들이 있는지 (즉, 분리가능하지 않은 상미분 방정식들), 음형태의 상미분 방정식 중 완전 상미분 방정식을 제외하고 남은 상미분 방정식들은 어떤 것들이 있는지 (즉, 완전하지 않은 상미분 방정식들) 쓰시오.
즉.
양형태의 상미분 방정식의 전체 집합을 W.
음형태의 상미분 방정식의 전체 집합을 U,
분리가능한 상미분 방정식의 전체 집합을 A,
완전 상미분 방정식의 전체 집합을 B
라고 할 때
집합 A^c ᑎ W 과 집합 B^c ᑎ U 에 대해 기술하는 문제이다. 그 집합에 해당하는 미분 방 정식의 예를 몇 개 구하고 그들의 공통된 특징을 기술하는 방법을 써도 좋고, 아니면 이 집 합에 속하는 방정식들의 특징을 바로 기술하여도 좋다.“

답글 달기