일상 속 알고리즘, 정렬에서 이어집니다.
앞서 직관적인 정렬인 버블정렬, 선택정렬, 삽입정렬에 대해 이야기했다. 이 세 정렬의 직관적인 모습은 다르지만 기본적으로 배열의 모든 값을 한 번씩 꺼내어, 다른 요소들과 전부 비교하는 알고리즘이다. 때문에 n(사실 n-1)개의 요소를 가져와서 요소 m(m=n개 중 이미 비교한 적 있는 요소를 제외한 나머지)개와 비교하는 형태로 시간복잡도가 O(n2)이다.
효율적인 방법으로 해결하지 못하면, 잠을 못 자는 개발자들에 의해 우리는 지금부터 n2에서 벗어나는 방법들을 탐구할 것이다. 그 중 첫 번째 주자는 토니 호어가 고안한 영국산 알고리즘, 퀵 정렬(Quick Sort)이다.
퀵 정렬(Quick Sort)
퀵 정렬은 이름에서 알 수 있듯이, 다른 정렬에 비해 빠른 정렬이다.(물론 당시에는 말이다) 퀵 정렬을 만드는 과정은 정렬된 배열을 BST로 만드는 과정과 닮은 점이 많다.
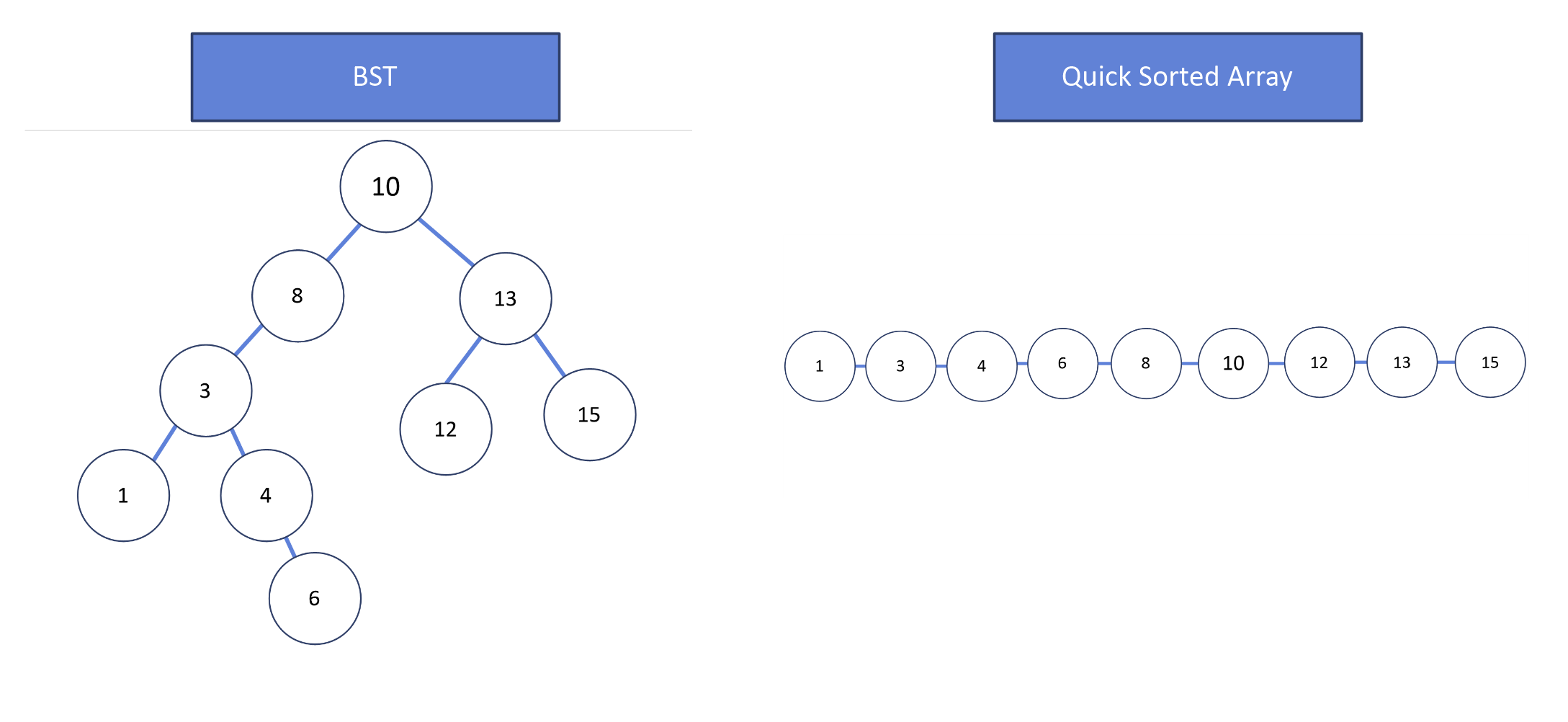
정렬된 배열로 BST를 만드는 과정은 중간 값을 루트로 설정해 배열과 함께 인자로 넣고, 해당 값의 앞 배열을 자른 뒤 그것을 인자 값으로 재귀로 함수를 호출하여 left 값으로 가리킨다. 마찬가지로 뒷 배열을 잘라 인자 값으로 재귀함수를 호출해 right값으로 가리킨다.
BST의 경우 정렬하는 것은 별개의 얘기지만, 퀵 정렬도 유사한 과정을 거친다. 퀵 정렬도 한 값을 기준으로 나머지 값들이 이 값보다 큰 지, 작은 지를 비교하는 지를 기본으로 한다. 흔히 피봇값이라 부르는 값을 배열에서 하나 선정해 그 보다 큰 값들을 모아놓고, 작은 값들을 모아 놓는다. 그리고 각자 모아놓은 그 값들이 이루는 배열을 가지고 새로운 피봇값을 정하여 또 피봇보다 작은 값들의 배열과 큰 값들의 배열을 나눈다. 이 과정을 재귀로 호출하며 반복한다.
퀵 정렬의 구현
# 퀵 정렬 선언.
# 정렬할 배열(재귀 시 피봇값의 앞-뒤 배열)과 해당 배열의 0번째, 마지막 인덱스를 인자로 받는다.
def quicksort(lst, start, end):
# 파티션 함수 선언.
# 인자 값으로 나눌 배열, 해당 배열의 0번째 인덱스를 ps, 마지막 인덱스를 pe 인자로 받는다.
# 언뜻보면 quicksort함수와 partition함수가 중복처럼 보일 수 있다.
# 퀵 정렬 함수의 재귀 호출과정에서, partition 함수를 통해 피봇값을 반환하고
# 해당 값을 받아 가공한 값을 재귀함수의 인자로 활용한다.
def partition(part, ps, pe):
# 정렬할 부분의 끝 값을 피봇값으로 저장
pivot = part[pe]
# ps는 정렬할 배열의 0번째 인덱스이다. 정렬할 배열의 기준에서는 0번째이지만
# 전체 배열에서는 0이 아닌 경우가 대부분이다.
# 때문에 ps-1은 정렬할 배열 밖의 인덱스이다.
1=ps-1
# ps가 가리키는 값에서 pe가 가리키는 직전까지의 값들을 j에 넣으면서 순회
# pe가 가리키는 값은 피봇값
for j in range(ps, pe):
# 인덱스 j 위치의 값이 피봇값보다 작으면
if part[j] <= pivot:
# i 값을 하나 올리고, 인덱스 i인 값과 인덱스 j인 값을 교환
# 만약 항상 part[j]<=pivot이라면, i값은 항상 j값과 일치하므로, 교환 의미가 없음.
# i=0, j=1인 경우, part[0] > pivot이라는 의미
# 그 때, part[j=1] <=pivot이라면, prat[i=0]과 part[j=1] 값을 교환한다.
i +=1
part[i], part[j] = part[j], part[i]
# 피봇값과의 비교를 마치면, 피봇값의 위치를 찾아주기 위한 교환 진행
# part[i]는 가장 최근에 part[j]와 교환한 피봇 값보다 작은 값이 저장되어 있다.
# 때문에 i보다 작은 인덱스 값은 피봇값보다 작은 값을 가리키고, i보다 큰 인덱스는 피봇값보다 큰 값을 가리킨다.
# part[i+1]과 part[pe]를 교환하면, 피봇값의 위치를 찾는 교환이 이뤄진다.
# 피봇값보다 큰 값들의 정렬은 신경쓰지 않는 교환이다.
part[i+1], part[pe] = part[pe], part[i+1]
# 현재의 피봇값의 인덱스를 반환한다.
return i+1
# 퀵 정렬 함수의 시작 인덱스 값이, 엔드 인덱스 값과 동일하거나 오히려 넘어가면 재귀 호출 없이 함수 종료
# 직전의 피봇값이 part의 맨 앞에 있거나, 맨 뒤에 있는경우에 해당한다.
if start >= end:
return None
# p는 partition 함수의 결과로 피봇값의 인덱스를 반환한다.
p = partition(lst, start,end)
# 피봇값의 앞 배열을 lst로 퀵정렬을 재귀호출한다.
quicksort(lst, start, p-1)
# 피봇값의 뒷 배열을 lst로 퀵정렬을 재귀호출한다.
quicksort(lst, p+1, end)
# 정렬된 배열을 반환한다.
return lst해당 함수는 오름차순의 퀵 정렬이다. 그리고 항상 가장 뒤의 값을 피봇값으로 선택하는 로무토파티션을 따른다. 퀵 정렬의 핵심은 함수를 실행할 때마다 정해지는 것이피봇값과의 비교결과와 피봇값의 인덱스 뿐이라는 것이다. 때문에 두 내용에 해당하지 않은 부분은 전부 정렬되지 않은 상태를 가정하고 연산이 이루어진다. 피봇값보다 작은 값을 찾아서 앞의 인덱스로 교환할 때, 피봇값의 인덱스를 찾을 때마다 교환의 반대 대상인 인덱스 값은 제대로 정렬됐는지 여부가 중요하지 않다.
배열 [3, 4, 1, 5, 2]를 퀵 정렬(오름차순, 로무토 파티션)하면 아래와 같다.
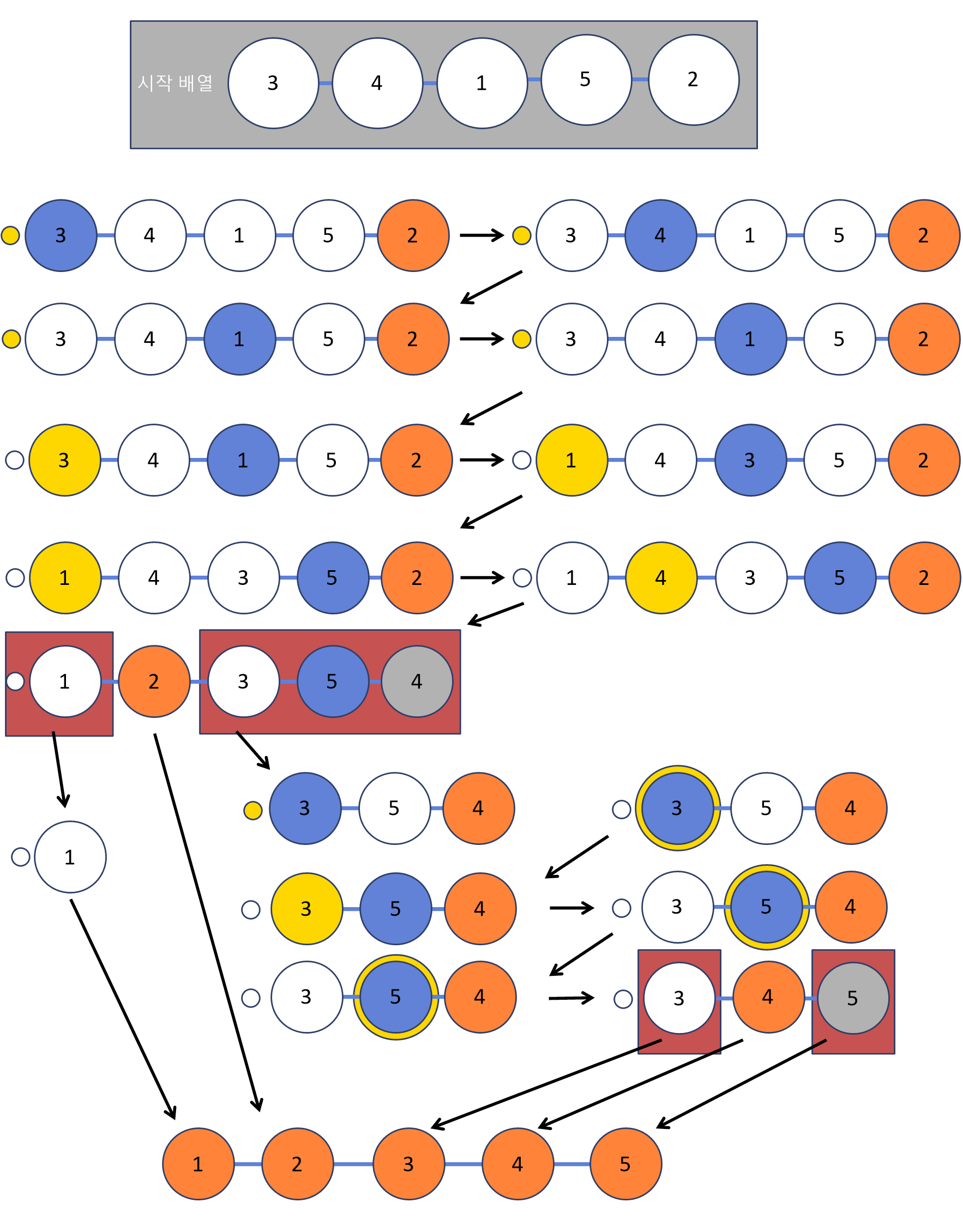
퀵 정렬의 시간복잡도
퀵 정렬의 시간복잡도는 정렬할 배열의 정렬상태에 따라 큰 차이를 보인다. 함수의 호출마다, 피봇값이 정렬을 2분하는 경우에는 O(n log n)의 시간복잡도를 갖는다.(ex, [1, 4, 2, 3, 6, 7, 10, 9, 8, 5]). 하지만 정렬된 배열을 퀵 정렬하는 경우 버블정렬과 마찬가지로 O(n2)의 시간복잡도를 갖는다.
마무리
To Be Continued . . . 2
