투 포인터란?
- 리스트에 순차적으로 접근해야 할 때 두 개의 포인터를 이동하면서 처리하는 알고리즘입니다.
- 포인터를 이동한다는 의미는 변수에 특정 인덱스 값을 저장하고, 그 인덱스 값을 바꿔주는 것 입니다.
- 시작점과 끝점 혹은 오른쪽과 왼쪽에 두 포인터 지점을 기준으로 하는 것이 일반적입니다.
예시
#리트코드 344.Reverse String
def reverseString(self, s: List[str]) -> None:
left, right = 0, len(s) -1
while left < right:
s[left], s[right] = s[right], s[left]
left += 1
right -= 1#리트코드 5.Longest Palindrome Substring
def longestPalindrome(self, s:str) -> str:
def expand(left: int, right: int) -> str:
while left >= 0 and right < len(s) and s[left] == s[right]:
left -= 1
right +=1
return s[left + 1:right]
if len(s) < 2 or s == s[::-1]:
return s #리트코드 1. Two Sum
def twoSum(self, nums : List[int], target: int) -> List[int]:
left, right = 0, len(nums) - 1
while not left == right:
if nums[left] + nums[right] < target:
left +=1
elif nums[left] + nums[right] > target:
right -= 1
else:
return [left, right] #리트코드 42. Trapping Rain Water
def trap(self, height: List[int]) -> int:
if not height:
return 0
volume = 0
left, right = 0, len(height) -1
left_max, right_max = height[left], height[right]
while left < right:
left_max, right_max = max(height[left], left_max),
max(height[right], right_max)
if left_max <= right_max:
volume += left_max - height[left]
left +=1
else:
volume += right_max - height[right]
right -= 1
return volume
#리트코드 15. 3Sum
def threeSum(self, nums: List[int]) -> List[list[int]]:
results =[]
nums.sort()
for i in range(len(nums) -2):
if i > 0 and nums[i] == nums[i - 1]:
continue
left, right = i + 1, len(nums) - 1
while left < right:
sum = nums[i] + nums[left] + nums[right]
if sum < 0:
left +=1
elif sum > 0:
right -=1
else:
results.append(nums[i], nums[left], nums[right])
while left < right and nums[left] == nums [left + 1]:
left += 1
while left < right and nums[right] == nums[right - 1]:
right -= 1
left += 1
right -= 1
return results
구조

사용방법
-
설계
리스트의 길이(혹은 순환할 리스트 안 부분의 길이)에 대응하여 실행되는 반복작업, 반복작업이 실행될 조건, 각 포인터들의 이동 조건을 설계해야합니다. 그리고 데이터(리스트)의 소트 작업이 정말 중요합니다. -
포인터 작동범위 설정해야합니다.
-
접근할 리스트 내 부분의 인덱스값(0, len(list_part))을 두 변수에 저장합니다.
예) left, right = 0, len(list) -
포인터 종료조건을 설정해야 합니다. 일반적으로 두 포인터가 만나는 시점 혹은 교차되는 시점을 종료 조건으로 설정합니다. 두 포인터가 만난다는 것은 같은 인덱스 값을 저장한다는 의미이고, 교차된다는 것은 인덱스의 낮은 값을 담은 변수(포인터)가 높은 값을 담은 변수보다 높은 인덱스 값을 담게 됨을 의미합니다.
예) while left < right:
-
포인터의 작동범위를 설정했으면, 작동원리 또한 정해야합니다.
작동원리에는 이동조건, 이동값이 포함됩니다.
예)while left < right and nums[left] == nums [left + 1]:
left += 1 -
작동원리까지 설정했으니, 마치 함수의 반환문(return)처럼 포인터도 특정 값을 전달한다는 본래의 목적을 달성해야합니다. 전달할 값 혹은 값의 조건을 설정하고, 값을 담을 변수도 선언해야합니다.
효용
2중 반복문을 사용하는 문제를 O(n)으로, 3중 반복문을 사용하는 문제를 O(n2)로 처리하도록 합니다. 효과적으로 사용하면 최고차항의 차수를 줄일 수 있다는 얘깁니다!
부르트포스와 투 포인트
부르트 포스(무차별 대입 or 막 해보기)와 비교하여 표현하면 다음과 같습니다.
상황 : list = [1, 3, 4, 5, 8, 11, 13] 인 배열에서 더해서 8이되는 두 값을 찾아라!
브루트 포스의 경우
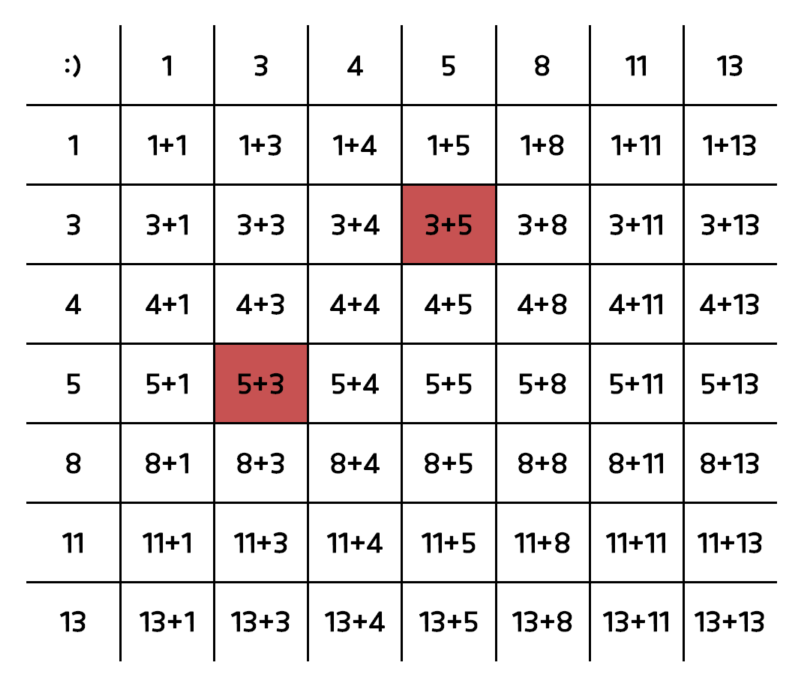
투 포인트의 경우
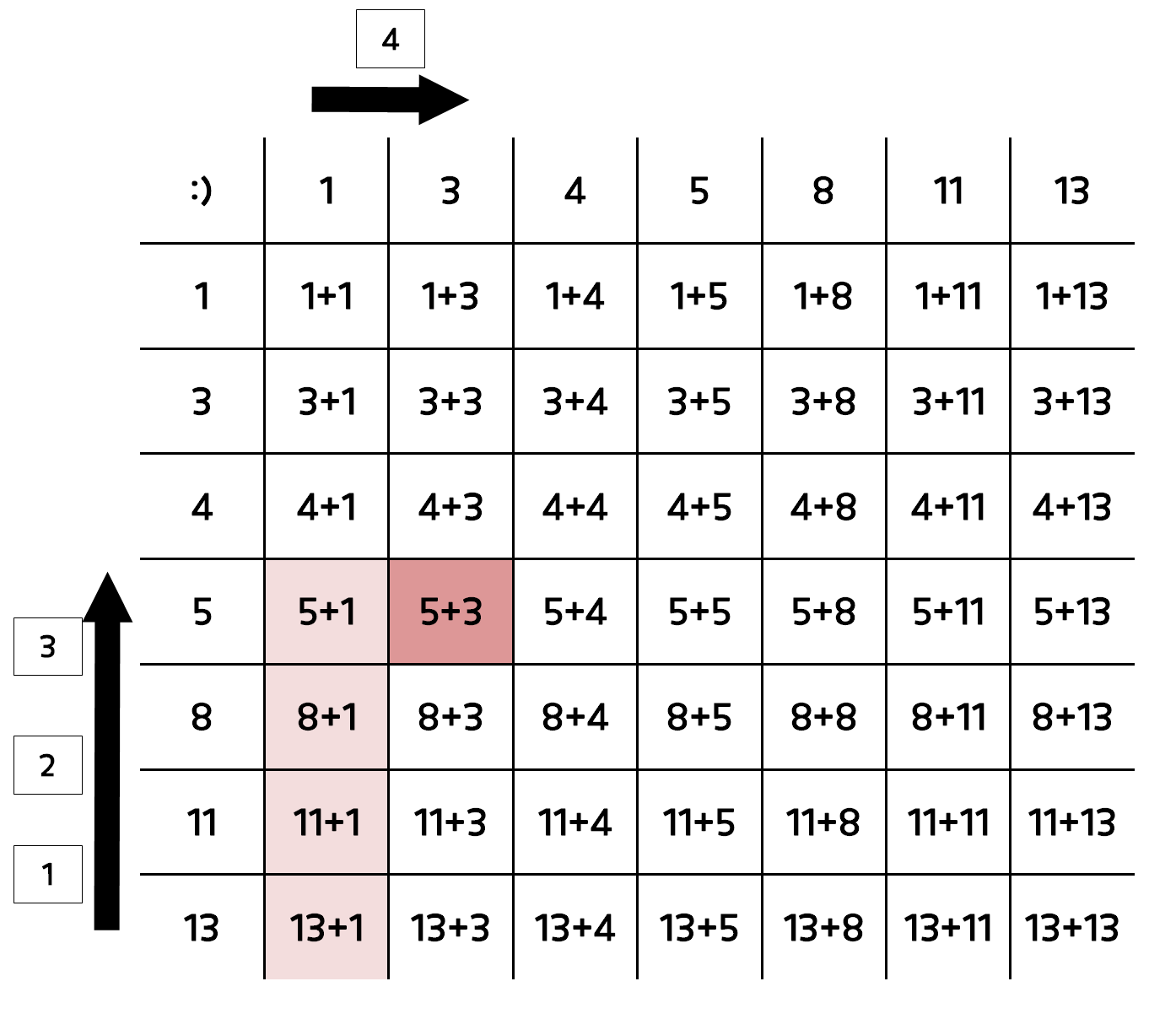
- 부르트 포스의 경우 49(7*7)번의 연산을, 투 포인트의 경우 고작 5번의 연산으로 원하는 값을 찾았습니다.(포인트 이동은 4번)
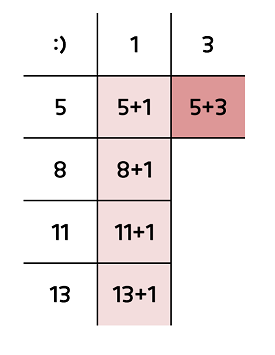
- 물론 원하는 값이 2나 26이었다면, 투 포인트 방식의 연산이 7번까지 늘어날 수 있었습니다.
- 무작정 반복해서 n개의 모든 값을 펼처놓고 계산한다면 n*n = n2번 계산했을 문제를, n번 이하의 계산으로 줄여준다는 것이 한 눈에 보이네요!
마무리로 몇 자만 더..
익숙해지면 그 만큼 다른 알고리즘과 연계하거나, 예외처리로 코드의 효율을 높일 수 있습니다. 이런 유연한 대처가 가능한 이유는 자료형의 정렬에 있습니다. 포인터를 움직인다는 것이 특정 기준에 대어보니 이전 값들에게는 예외가 발생할 여지가 없다고 판단하는 것입니다. 기준 판단의 횟수를 줄이기 위해, 일상적인 것이 오름차순(혹은 내림차순)을 비롯하여 주어진 모든 값을 정렬하는 것입니다. 그러니, 가급적이면 인자값을 정렬해서 사용합시다.
투 포인트라는 이름은 사전적인 정의가 있는 기법이라기보다, 예전부터 자주 사용하는 문제풀이 방식에 적당히 직관적인 이름을 붙였다고 할 수 있습니다.(마치, 머리를 쏙 내밀고 치는 헤엄 = 개헤엄이라 부르는 것과 유사) 이런 용어들의 특징은 그 모호함에도 불구하고, 자주 언급된다는 점에 있습니다. 그 만큼 유용한 풀이방식인 만큼, 빨리 친해집시다! :)

