최단경로는 가장 짧은 거리를 찾는 알고리즘이다. 가장 가까운 물리 노드에 저장된 값을 찾는 것은 아니고, 거리 값 혹은 이동 비용 등으로 입력된 값 중에 가장 낮은 값을 반환하는 것이다. 때문에 일반적인 그래프에 비해 이상적인 자료구조에서 더욱 벗어난 알고리즘이다.
시작점에서 각 지점까지의 최단경로
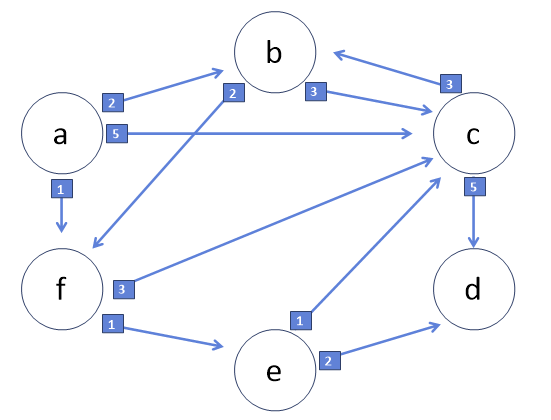

현실에서 최단경로는 알고리즘의 영역이 아니다. 현실에서 최단경로라 하면 물리적으로 얼마나 떨어져있나를 얘기하기 때문이다. 그렇다면 최단경로는 현실에서 어떻게 적용할 수 있을까. 버스 정류장 사이에 몇 개의 정류장이 있는지를 바탕으로, 시작 정류장에서 각 정류장까지 거쳐야하는 최소한의 정류장 수를 구하는 경우에 적용할 수 있다.
다익스트라 알고리즘
다익스트라 알고리즘은 위와 같은 최단경로 문제에 접근하기 위해 에츠허르 다익스트라가 만든 알고리즘이다. 알고리즘의 원리는 각 노드 사이 직접 연결 값을 업데이트하고, 직접 연결 값을 바탕으로 간접 연결 값을 계산하여 가장 작은 값으로 갱신하는 알고리즘이다.
다익스트라 알고리즘 구현
# 무한대 값 선언
INF = int(1e9)
# 다익스트라 알고리즘 함수 선언
def dijkstra_naive(graph, start):
# 최소 비용 반환 함수 선언
def get_smallest_node():
# 최소 값 받을 변수 min_value 선언, INF로 초기화
min_value = INF
# 인덱스 값 0으로 초기화
idx = 0
# 그래프의 모든 정점을 순회
for i in range(1, N):
# 정점에 대한 도달 최소 비용의 현재 저장값과 비교 값을 비교하여
# 현재 저장 값(min_value)이 크면, 비교 값(dist[i])로 갱신
# get_smallest_node함수가 호출 될 때마다, 방문하지 않은 정점 하나에 대해
# min_value를 갱신
if dist[i] < min_value and not visited[i]:
min_value = dist[i]
# 값이 갱신되면 인덱스를 i값으로 갱신
idx = i
# 최종 갱신된 idx값 반환
return idx
# 정점 수를 N으로 저장
N = len(graph)
# 방문 여부를 확인하는 배열 선언
visited = [False]*N
# 각 정점에 대한 최소 도달 비용 저장하는 배열 선언
dist = [INF]*N
# 시작 정점의 방문여부와 도달비용을 갱신
visited[start] = True
dist[start] = 0
# 그래프를 시작점을 키 값으로 순회
# adj는 가리키는 정점, d는 비용을 저장
for adj, d in graph[start]:
# adj에 최소 도달 비용 d로 갱신
dist[adj] = d
# 모든 정점에 대해 순회
for _ in range(N-1):
# 시작 정점에 연결된 정점들을 순회하며, 갱신된 인덱스 값 cur에 저장
cur = get_smallest_node()
# 최소값 갱신된 정점에 대한 방문여부 갱신
visited[cur] = True
# 갱신 된 정점에 대하여
# 연결된 정점과 시점에서의 도달비용을 순회
for adj, d in graph[cur]:
# 이동 비용 저장
cost = dist[cur] + d
# 현재 정점을 지나는 이동 비용과 이동할 정점에 대한 최소 이동비용을 비교
if cost < dist[adj]:
# 현재 정점을 지나는 이동 비용이 더 작으면 갱신
dist[adj] = cost
# 각 정점에 대한 최소 이동비용을 반환
return dist
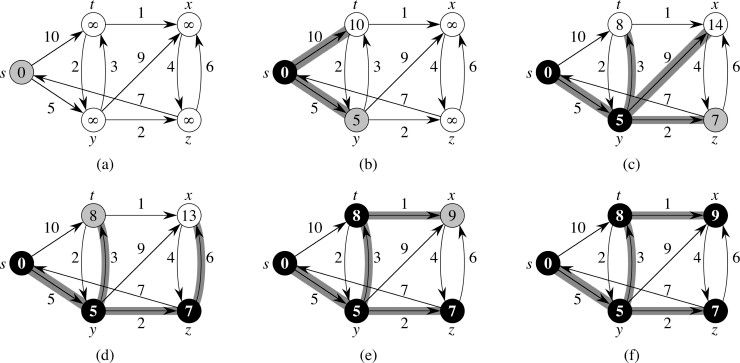
다익스트라 알고리즘의 파이썬 구현 코드이다. 해당 배열에 최소도달비용을 저장하기 위해 정점의 수만큼을 길이로 하는 배열을 선언하고, 무한히 큰 값인 INF를 요소로 저장한다. 순환으로 가리키는 정점이 있을 수 있기 때문에, 방문 여부를 확인하기위한 배열도 선언한다. 시점의 이동 비용을 0으로 갱신하고, 시점에서 직접 연결된 정점들부터 비용을 차례로 갱신한다. 그 후 모든 정점을 순회하며 이중반복문을 실행한다. 이중 반복문은 방문할 정점을 찾아서 반복표시를 하는 반목문과 방문한 정점에 연결된 정점과 비용을 가져와 최소비용을 계산하는 반복문으로 이루어져있다.
방문할 정점을 찾는 함수는 방문비용이 가장 작은 인덱스를 찾는다. 시점으로부터의 직접 연결비용만 입력되었을 때는, 시점으로부터 가장 가까운 점부터 호출되는 것이다.
시점으로부터 출발해 방문한 정점에 연결된 정점까지의 계산을 하는 반복문은 시점으로부터 연결된 정점까지 직접 연결비용과 (시점에서 k까지의 비용+k에서 방문점까지 비용)을 비교하여 더 작은 값으로 갱신하는 반복문이다. 계산이 어느정도 진행된 이후에는, 현재 저장된 최소값과 (시점에서 k까지의 비용+k에서 방문점까지 비용)을 비교하여 최소값을 저장하게 된다.
# 힙큐 모듈 수신
import heapq
# 다익스트라 함수 선언
def dijkstra_pq(graph, start):
# 정점의 길이를 저장
N = len(graph)
# 최소 도달 비용 저장 배열 선언, INF로 초기화
dist = [INF]*N
# 큐 선언, 큐는 방문할 정점을 담는 큐
q=[]
# 큐에 시작점을 푸쉬
heapq.heappush(q, (0, start))
# 시작점의 도달비용 갱신
dist[start] = 0
# 모든 연결된 정점을 순회할 때까지 반복
while q :
# 정점까지의 이동 비용과 연결된 정점을 변수에 저장(갱신)
acc, cur = heapq.heappop(q)
# 만약 연결된 정점에 대한 이동 비용이 해당 노드에 대한 현재 도달 비용보다 크면,
# 해당 정점에 대한 계산은 생략하고, 반복문 순회
if dist[cur] < acc:
continue
# 연결된 정점에 대해, 연결 정점과 이동비용 저장
for adj, d in graph[cur]:
# 직전 정점에서의 이동 비용과 연결 정점을 더하여 cost에 저장
cost = acc + d
# 만약 cost가 현재 최소도달비용보다 작으면
if cost < dist[adj]:
#cost의 값으로 최소도달비용 갱신
dist[adj] = cost
# 현재 정점과 최소도달비용을 q에 푸쉬
heapq.heappush(q, (cost,adj))
# 최소 도달비용을 저장한 배열 반환
return dist다익스트라 알고리즘의 내장모듈인 힙큐를 활용한 파이썬 구현코드이다. 위의 구현코드와 큰 차이가 있지는 않지만, 힙큐를 활용하여 현재 최소 이동 값을 저장하고 있는 정점을 찾는 비용을 n에서 log n으로 낮춘 형태의 구현코드이다.
모든 점을 시점으로 각 정점까지의 최단경로
위의 최단경로와 다르게 시작점이 정해지지 않은 알고리즘이다. 각 이동에 대한 최단경로를 구해놓고 비교하거나, 원할 때 검색하는 형태로 활용할 수 있다. 결과값을 생성하는 비용은 큰 것에 비해, 탐색하는 비용은 비교적 저렴하다. 때문에 미리 연산하여 새로운 데이터로 활용하여 검사하는 방식으로 활용이 가능하다. 일상적인 문제에서는 첫 일정이 정해지지 않은 여행 경로를 계획하는 경우에 동선을 계산하는 형태로 이해할 수 있다.
플로이드-워셜 알고리즘
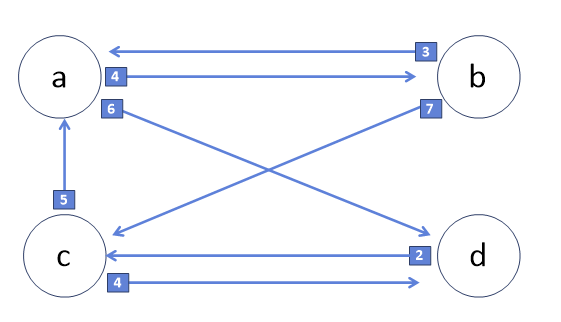



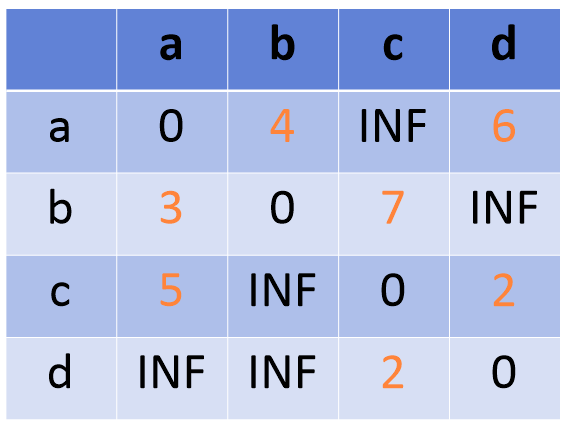
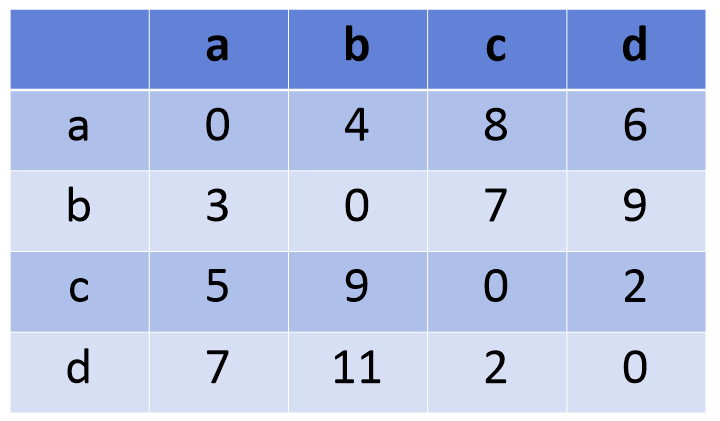
플로이드가 구현한 알고리즘으로 그래프에서 가능한 모든 두 점에 대한 최단 거리를 구하는 알고리즘이다. 알고리즘의 원리는 정점의 수 만큼의 길이를 갖는 배열을, 정점의 수 만큼 갖는 이중배열을 선언하고 모든 값을 무한히 큰 값 INF에서 점차 갱신하는 것이다. 정점에서 같은 정점으로 이동하는 비용을 0으로 그래프를 참고하여 직접연결된 정점으로 이동하는 비용을 갱신한 뒤에, 다른 정점 하나를 거친 비용과 비교하여 작은 값으로 갱신한다.
플로이드-워셜 알고리즘 구현
# dist 초기화용 INF 선언
INF = int(1e9)
# 플로이드 워셜 알고리즘 함수 선언
def floyd_warshall(graph):
# 정점의 수를 N에 저장
N = len(graph)
# 도달비용을 나타낼 길이 N의 배열을 N개만큼 인접행렬의 형태로 생성
# 모든 값은 INF로 생성
dist = [[INF]*(N+1) for _ in range(N+1)]
# 인접행렬을 순회하면서 출발점과 도착점이 같은 경우,
# 이동 비용을 0으로 설정
for idx in range(1, N+1):
dist[idx][idx] = 0
# 그래프를 순회하면서 각 정점에 저장된 키 값(start)과 밸류 값(adjs)을 저장
for start, adjs in graph.items():
# 시작점(start)와 직접연결 된 밸류 값(adjs)을 순회
# adj는 정점, d는 이동비용
for adj, d in adjs:
# dist의 start(시작점)번째 배열의 adj(도착점)번째 배열의 값을 d로 갱신
# (시작점에서 도착점으로 가는 비용 입력)
dist[start][adj] = d
# 모든 정점을 k로 순회
for k in range(1, N+1):
# 모든 정점을 a로 순회
for a in range(1, N+1):
# 모든 정점을 b로 순회
for b in range(1, N+1):
# a점에서 b점으로 가는 비용과 (a점에서 k점으로 가는 비용 + k점에서 b점으로 가는 비용)을 비교
# a점에서 b점으로 가는 비용이 더 저렴하면, 갱신 없이 반복문 순회
# a점에서 b점으로 가는 비용이 더 비싸면, 갱신하고 반복문 순회
dist[a][b] = min(dist[a][b], dist[a][k] + dist[k][b])
# 이동 비용이 담긴 인접행렬을 반환
return dist파이썬으로 구현한 플로이드-워셜 알고리즘이다. 첫 번째 반복문에서 시점과 종점이 같을 때의 도달비용을 0으로 설정하고, 두 번째 이중반복문에서 그래프에 저장된 시점과 종점의 도달비용을 갱신한다. 세 번째 삼중 반복문에서는 기존 저장된 최소 도달비용과 다른 비용을 비교하여 작은 값을 저장한다. 다른 비용은 한 점 k를 선정해서 시점부터 k까지의 도달비용과 k에서 종점까지의 도달비용을 합한 비용이다.
알고리즘을 통한 이중배열 생성비용은 O(n3)이고, 검색 비용은 탐색 방법에 따라 다르지만 일반적으로 O(n2)이다.
마무리
지도 앱이 없던 그 시절의 내가 떠오른다
