정규화
주어진 릴레이션 스키마를 함수적 종속성과 기본키 기반으로 분석해 수정, 삽입, 삭제 이상을 최소화하기 위해서 테이블을 분해하는 과정이다.

정규화의 장점
- 정규화 단계가 진행될수록 중복이 감소하고 갱신 이상도 감소된다.
정규화의 단점
- 정규화가 진행될 때마다 하나의 테이블이 최소 두개 이상으로 분해된다. 분해된 테이블을 대상으로 질의할 때, 같은 정보를 얻기 위해서 보다 많은 테이블들을 접근해야 되므로 조인의 필요성이 증가한다.
역정규화
응용의 요구사항에 따라 데이터베이스 설계의 일부분을 역정규화함으로써 데이터 중복 및 갱신 이상을 대가로 치르고 성능상의 요구를 만족시킨다. 역정규화는 주어진 응용에서 빈번하게 수행되는 검색 질의의 수행 속도를 높이기 위해 이미 분해된 두 개의 릴레이션들을 합쳐 하나의 릴레이션으로 만드는 작업이다.
갱신 이상
수정 이상 : 반복된 데이터 중에 일부만 수정하면 데이터의 불일치가 발생한다.
삽입 이상 : 불필요한 정보를 함께 저장하지 못한다면 어떤 정보를 저장하는 것이 불가능하다.
삭제 이상 : 유용한 정보를 함께 삭제하지 않고는 어떤 정보를 삭제하는 것이 불가능하다.
나쁜 설계 예시
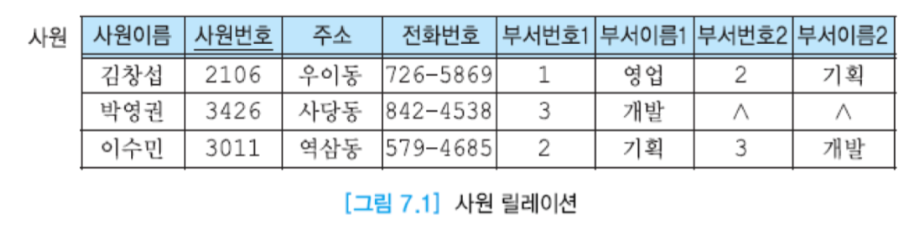
- 부서 이름 중복(부서이름1, 부서이름2), 한 사원이 세 부서 이상 속하게 되면 추가하기 어려움

- 하나의 사원에 대한 정보가 통째로 중복되어 있다. 속해 있는 사원이 없다면 새로운 부서 삽입이 어려워지고, 영업부서의 김창섭을 해고한다면 영업부서의 정보가 아예 사라지게 된다.
- 수정이상 : 부서의 이름이 바뀔때, 속한 사원의 튜플에서만 부서 이름을 변경하면, 데이터베이스 불일치가 발생한다. (똑같은 데이터가 여러군데 존재하므로 모두 수정하기 어려움)
- 삽입이상 : 새로운 부서를 신설할 경우, 사원이 존재하지 않으면 부서 정보를 입력할 수 없다.
- 삭제이상 : 부서에 속한 사원이 한명일 경우, 이 사원을 삭제하면 부서에 관한 정보까지 같이 삭제된다.
함수적 종속성과 결정자
- 함수적 종속성 : 테이블의 특정 칼럼 A를 알면 다른 칼럼 B값을 알 수 있을 때, 칼럼 B는 칼럼 A에 함수적 종속성이 있다고 말한다.
- 결정자 : 함수적 종속성 설명에서 칼럼 A를 결정자라고 말한다. (A->B, A가 B를 결정한다.)
완전 함수적 종속성
A에 B가 함수적으로 종속하면서 A의 어떠한 진부분 집합에도 함수적으로 종속하지 않을 때
이행적 함수적 종속성
A->B이고 B->C이면 A->C이다.
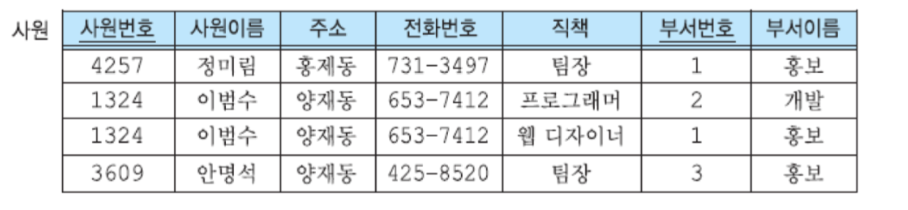
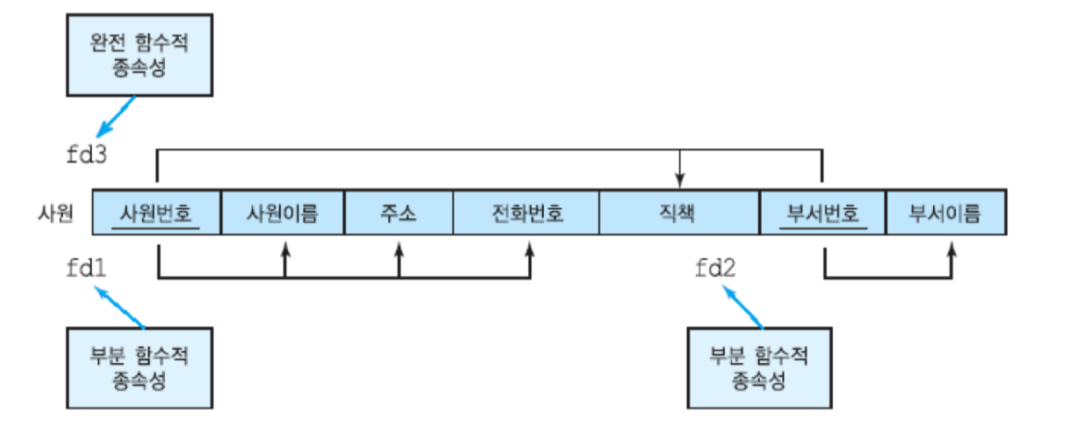
- 사원 테이블에서의 함수적 종속성
- 사원번호 -> 사원이름, 주소, 전화번호
- 부서번호 -> 부서이름
- (사원번호, 부서번호) -> 직책
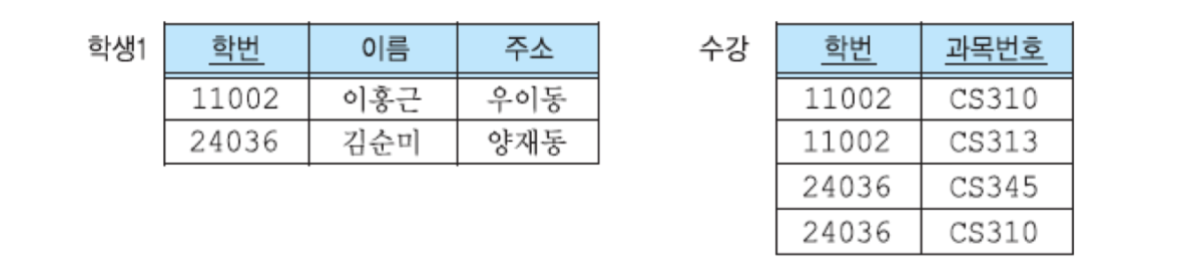
제 1 정규형
R의 모든 속성이 원자 값을 가진다.
- 과목번호가 원자 값을 갖지 않으므로 값마다 하나의 튜플로 분리한다.
- 속성을 분리해서 새로운 테이블에 넣는다.
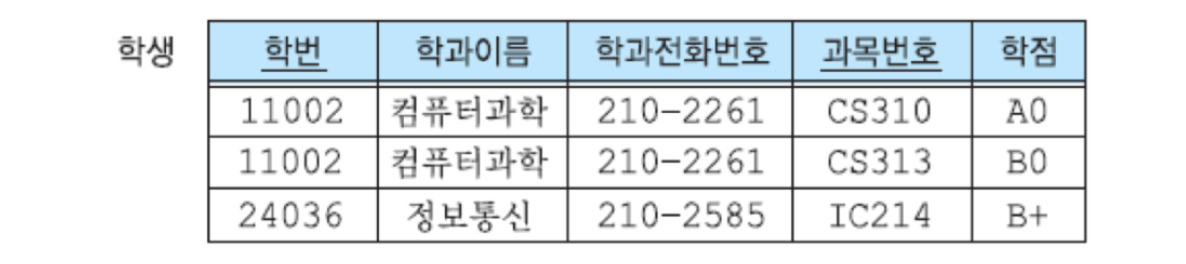
제 1 정규형에 존재하는 갱신 이상
- 수정이상 : 학과 학생 수만큼 학과전화번호 중복되는데, 학과전화번호가 변경되면 속한 모든 학생의 전화번호를 수정하지 않으면 데이터베이스의 일관성이 깨지게 된다.
- 삽입이상 : 학생이 없는 학과는 삽입할 수 없다. (학번이 기본키의 구성요소인데, 엔티티 무결성 제약조건으로 Null 값을 입력할 수 없다.)
- 삭제이상 : 어떤 학과에 소속된 마지막 학생을 삭제하면 학과에 대한 정보도 같이 삭제된다.
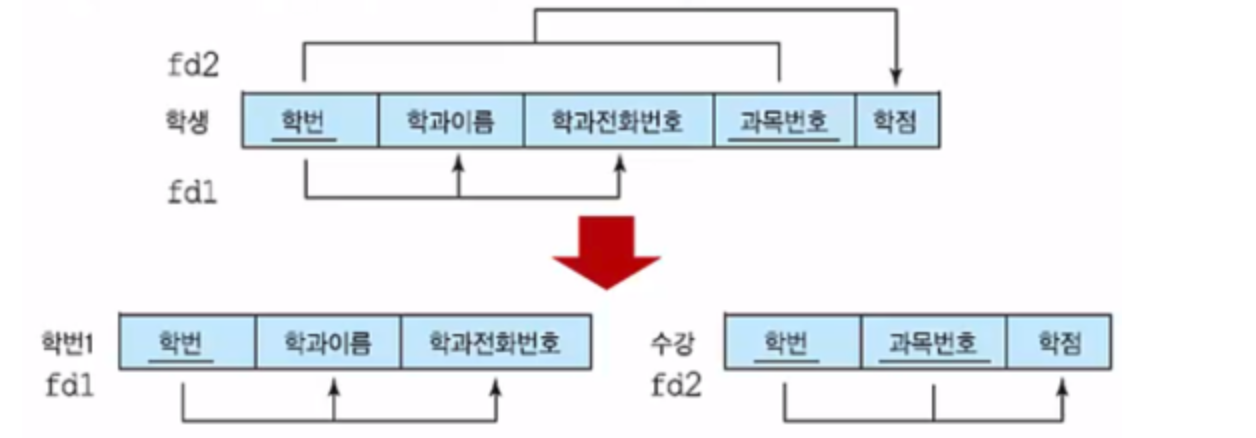
제 2 정규형
제 1 정규형을 만족하고 모든 속성들이 기본키에 완전하게 함수적으로 종속하는 것을 말한다. (부분적 종속성을 없앤것)
제 2 정규형에 존재하는 갱신 이상
- 수정이상 : 여러 학생이 소속된 학과의 전화번호가 변경되었을 때, 그 학과에 속한 모든 학생들의 투플에서 전화번호를 수정하지 않으면 데이터베이스의 일관성이 유지되지 않는다.
- 삽입이상 : 어떤 학과를 신설했는데 아직 소속된 학생이 없다면 그 학과의 정보를 입력할 수 없다. (학번이 기본키인데 엔티티 무결성 제약조건에 따라 기본키에 Null값을 입력할 수 없기 때문이다.)
- 삭제이상 : 어떤 학과에서 마지막 학생의 투플이 삭제되면 그 학과의 전화번호도 같이 삭제된다.
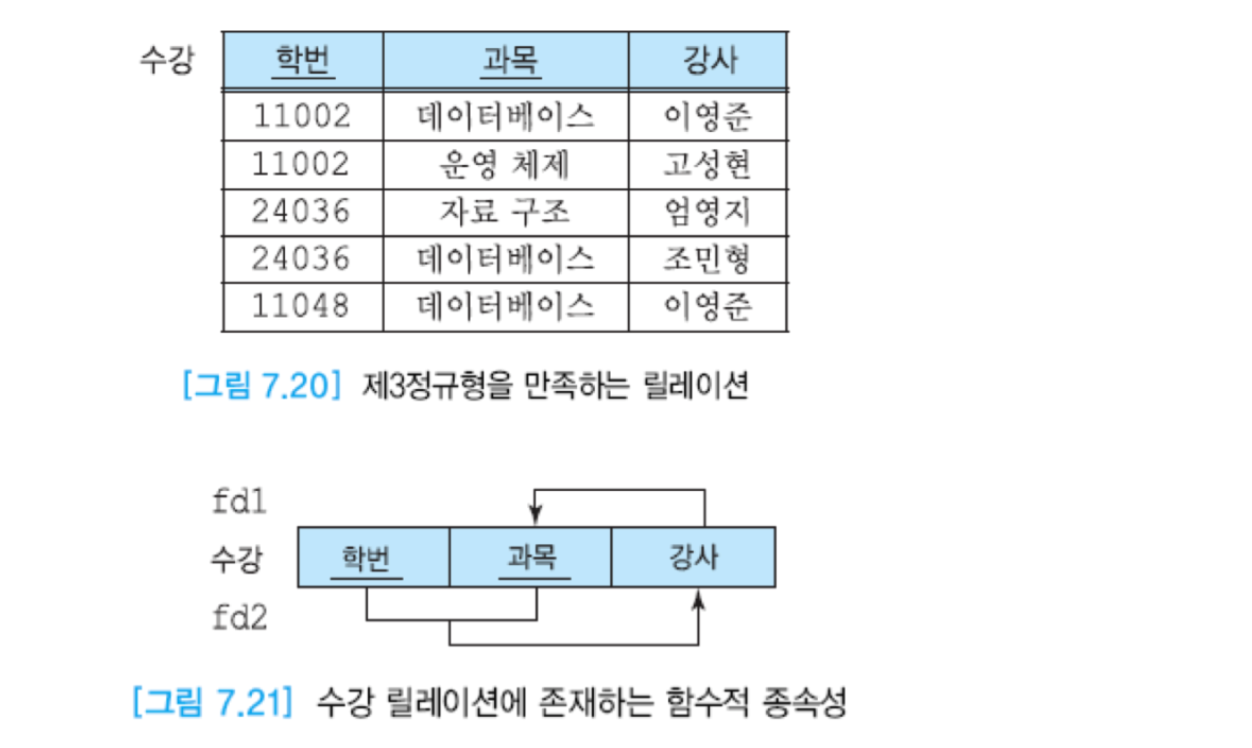
제 3 정규형
제 2 정규형을 만족하고 키가 아닌 모든 속성이 테이블의 기본키에 이행적으로 종속하지 않는 것을 말한다. (부분적 종속성, 이행적 종속성을 제거함)
제 3 정규형에 존재하는 갱신 이상
- 수정이상 : 여러 학생이 수강 중인 어떤 과목의 강사가 변경되었을 때, 그 과목을 수강하는 학생들의 투플에서 강사를 수정하지 않으면 데이터베이스 일관성이 깨진다.
- 삽입이상 : 신설하는 과목에 수강 학생이 없으면 해당 과목의 강사 정보를 입력할 수 없다.(학번이 기본키를 구성하므로 엔티티 무결성 제약조건에 의해 기본키에 널값을 삽입할 수 없다.)
- 삭제이상 : 어떤 과목을 이수하는 마지막 학생이 삭제되면 학과에 대한 정보도 같이 삭제된다.
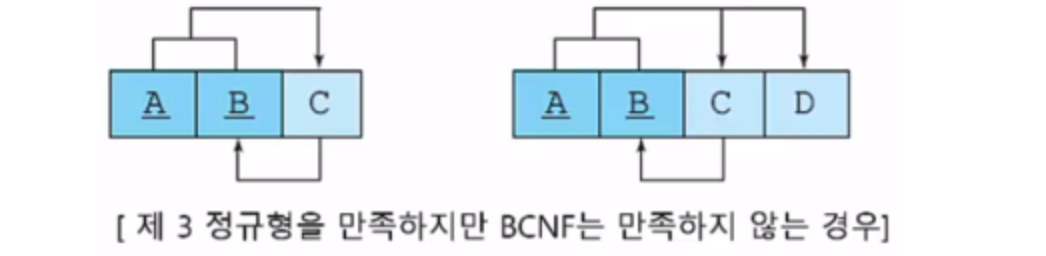
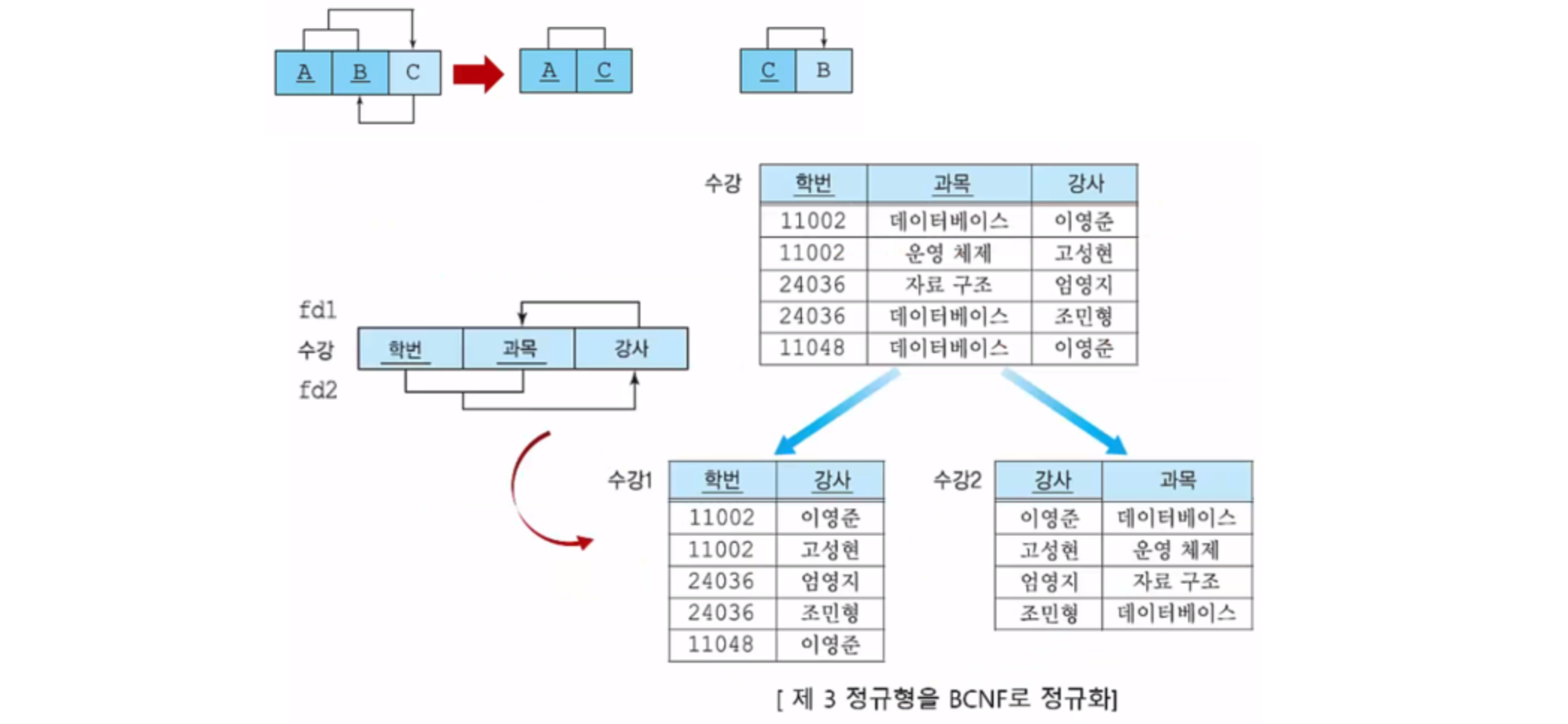
BCNF
제 3 정규형을 만족하면서 모든 결정자가 후보키여야 한다.
- 제 3 정규형을 만족하는 테이블을 BCNF로 정규화하려면 키가 아니면서 결정자 역할을 하는 속성과 그 결정자에 함수적으로 종속하는 속성을 하나의 테이블에 넣는다. 그리고 기존 테이블에 결정자를 남겨 기본 키의 구성요소가 되도록한다.