문제
접근
황선자씨와 모든 우주신들이 교감을 할 수 있도록 연결하는 문제이다. 이 통로들의 합이 최소가 되게 통로를 만들어야 하므로 최소신장트리 문제인 것을 알 수 있다.
최소신장트리 기본 문제에서는 정점1, 정점2, 둘 사이의 거리를 알려줬다면 이 문제에서는 정점들의 좌표들을 알려줬다.
- 좌표를 알려줬으니 각 정점들의 거리는 너가 계산해 라는 뜻으로 해석했다.
그래프 문제에서도 좌표를 사용하는 비슷한 문제가 있었는데 그 문제에서 모든 좌표들의 거리를 계산했던 적이 있어 쉽게 접근할 수 있었다.
정리하자면 정점 n개가 있다면 임의의 정점 u는 다른 정점 n-1개와 이어주는 새로운 그래프를 만들어줘야 한다.
임의의 한 좌표에서 다른 좌표까지 모두 도달할 수 있기 때문이다.
밑 그림과 같이 정점이 n개일 때 간선의 개수는 n(n-1)/2인 완전 그래프를 만드는 것이다.
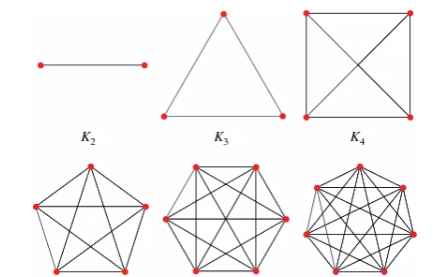
이후 M개 만큼의 초기에 이어져 있는 정점을 입력받는데 크루스칼 알고리즘을 사용하므로 두 정점을 Union을 해준다.
이 때 내가 틀렸던 부분은 초기에 이어진 정점이 같은 집합일 수 있다는 것이다.
예를 들면 (1,2), (2,3), (1,3)이 먼저 이어진 정점이라면 (1,2), (2,3) 두 번 Union되고 (1,3)은 같은 집합이므로 Union 되지 않는데 이런 케이스를 고려하지 않고 모두 Union한 개수를 셌다.
크루스칼 알고리즘에서 간선 개수 = (정점 - 1) 일 때까지 정점을 추가하는데 미리 간선의 개수를 더 count해서 모든 정점을 이어주지 못하였다.
이 부분만 주의하면 나머지 부분은 기본 크루스칼 알고리즘과 동일하게 풀 수 있다.
소스 코드
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
pair<int, int> god[1001];
int parent[1001];
int N, M, K;
int cnt = 0;
tuple<double, int, int> edges[500001];
int find(int u) {
if (parent[u] == u)
return u;
parent[u] = find(parent[u]);
return parent[u];
}
int Union(int u, int v) {
u = find(u);
v = find(v);
if (u != v) {
parent[u] = v;
return 1;
}
return 0;
}
void solve() {
int edgeIdx = 0;
for (int i = 1; i <= N; i++) { // 각 좌표 끼리의 거리를 구해 간선 만들기
for (int j = i + 1; j <= N; j++) {
int x = god[i].first - god[j].first;
int y = god[i].second - god[j].second;
long long dis = (ll)x * x + (ll)y * y;
edges[edgeIdx++] = { sqrt(dis), i,j };
}
}
sort(edges, edges + edgeIdx);
int idx = 0;
double sum = 0;
while (cnt < N - 1) { // 간선 개수가 정점 - 1개 일 때까지 진행
int u, v;
double dis;
tie(dis, u, v) = edges[idx++];
if (!Union(u, v)) //간선 추가되지 않았으면 다음 검사
continue;
cnt++; //간선 추가됐다면 개수+1, 간선 거리 합하기
sum += dis;
}
cout << fixed; // 소수점 둘째 자리까지 출력
cout.precision(2);
cout << sum;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cin >> N >> M;
for (int i = 1; i <= N; i++) { // 좌표 입력 받기
int x, y;
cin >> x >> y;
god[i].first = x;
god[i].second = y;
}
for (int i = 1; i <= N; i++) { // 그룹 초기화
parent[i] = i;
}
for (int i = 0; i < M; i++) { // 초기 이어진 정점
int v1, v2;
cin >> v1 >> v2;
if (Union(v1, v2)) // Union이 수행 됐을 때만 간선 개수 count
cnt++;
}
solve();
return 0;
}