이분 탐색(이진 탐색)
이분 탐색(Binary Search)
이진 탐색이란 정렬된 배열에서 특정 값을 찾는 탐색 알고리즘이다.
이진 탐색은 배열 중간을 기준으로 데이터를 탐색하기 때문에 반드시 데이터가 정렬된 상태로 존재해야 한다.
cf)앞에 입력한 원소보다 작은 값을 입력하면 다시 입력해야한다.
이분 탐색의 시간 복잡도는 O(logN)으로 배열을 전수 조사하는 O(N)에 비하면 상대적으로 빠른 탐색 알고리즘에 속한다. O(logN)만에 값을 찾을 수 있는 이유는 중간을 기준으로 탐색 대상을 절반씩 줄여나가기 때문이다.
이분 탐색은 어떻게 이루어 지는 가?
이진 탐색은 내가 찾고자 하는 값이 정렬된 배열의 중간 값보다 크면 중간값을 포함한 하위 값들은 탐색 대상에서 제외된다. 반대로 찾고자 하는 값이 배열의 중간 값보다 작으면 중간 값을 포함한 상위 값들은 탐색에서 제외된다.
요약하자면 중간값과 찾으려는 값의 대소를 비교한 뒤 탐색 범위를 반으로 줄여가며 값을 찾는 탐색 알고리즘이다.
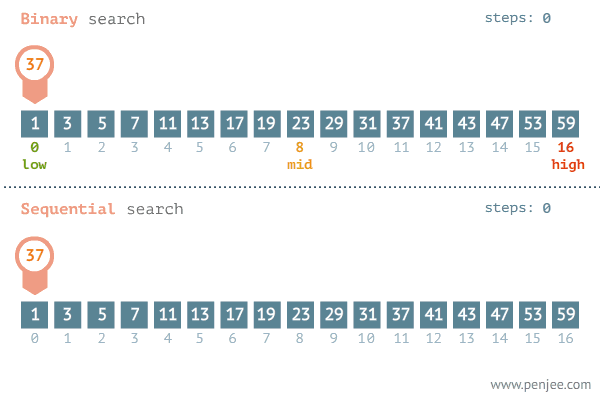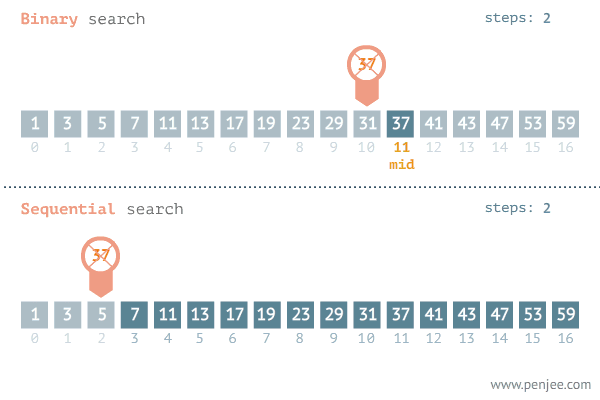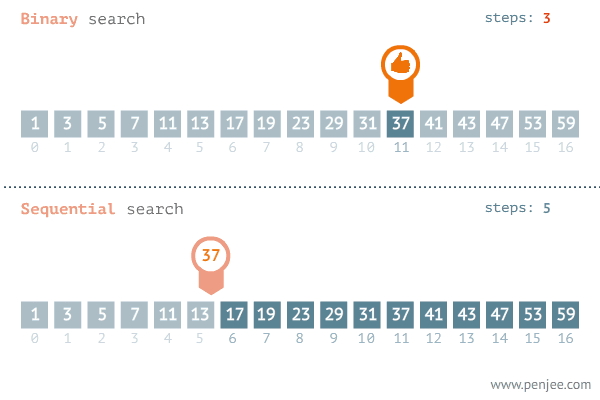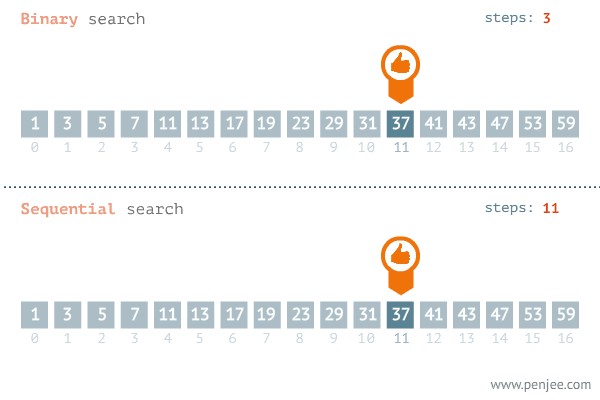
이분 탐색의 시간복잡도는?
운이 좋으면 찾고자 하는 값이 중간값과 동일해서 탐색이 끝나지만 최악의 경우 남은 데이터 하나가 될 때까지 탐색을 반복한다.
계산식으로 표현해보자
전체 데이터의 수를 N이라고 할 때
1) 첫 번째 탐색 후 절반만 남아 남은 수가 N/2개
2) 두 번째 탐색에서 다시 절반만 남아 남은 수가 N/2* 1/2개
3) 세 번째 탐색에서 다시 절반만 남아 남은 수가 N/2 1/2 1/2개
규칙을 보자면
k번째 탐색에서 남은 데이터의 수는 (1/2)^k*N이 된다.
최악의 경우에는 (1/2)^k*N = 1이 될 때까지 탐색을 하게 된다.
->k = log(2)N이 된다. 따라서 시간 복잡도는 O(log(2)N)으로 나타난다.
이분 검색의 알고리즘을 코드로
from typing import Any, Sequence
def bin_search(a: Sequence, key: Any) -> int:
#시퀸스 a에서 key와 일치하는 원소를 이진 검색
pl = 0 #검색 범위 맨 앞 원소의 인덱스
pr = len(a) - 1 #검색 범위 맨 끝 원소의 인덱스
