Time Complexity

• 1초 input 기준 알고리즘별 소요 시간

N: 인풋 갯수	알고리즘	소요시간	example
-	$O(1)$	1s	반복 없이 원큐에 실행 되는 것
-	$O(logN)$	1s	입력 N 을 받아서 반으로 계속 나눠가는 알고리즘 (e.g., binary search)
${1G}$	$O(N)$	1s	1 중 for 문
$5M$	$O(NlogN)$	1s	quick sort, merge sort, heap sort
$10K$	$O(N^2)$	1s	2중 for 문
$0.5K$	$O(N^3)$	1s	3중 for문
$20$	$O(2^N)$	1s	크기가 N인 집합의 부분집합
$10$	$O(N!)$	1s	크기가 N인 순열

---

O(1)

$O(1)$

• 반복없이 원큐에 실행되는 것

int sum = 0;
sum = N+(N+1)/2;

---

O(logN)

$O(logN)$

• 입력 N을 받아서 반으로 계속 나눠가는 알고리즘

• binary search

---

O(N)

$O(N)$

• 대표적으로 for 문

sum=0
for idx,val in enumerate(list):
    sum+=1

• 1초 소요 -> 입력(N): 1억($1*10^9$) $1G$개 라고 생각하면 될듯

---

O(NlogN)

$O(NlogN)$

• 1초 소요 -> 입력(N): 5백만($5*10^6$) $5M$개라고 생각하면 될듯

• quick sort
• merge sort
• heap sort

---

O(N^2)

$O(N^2)$

• 이중 for 문

for(int i=0;i<N;i++){
    for(int j=0;j<N;j++){
        do_something
    }
}

• 1초 소요 -> 입력(N): 1만($1*10^4$) $10K$개 라고 생각하면 될듯

---

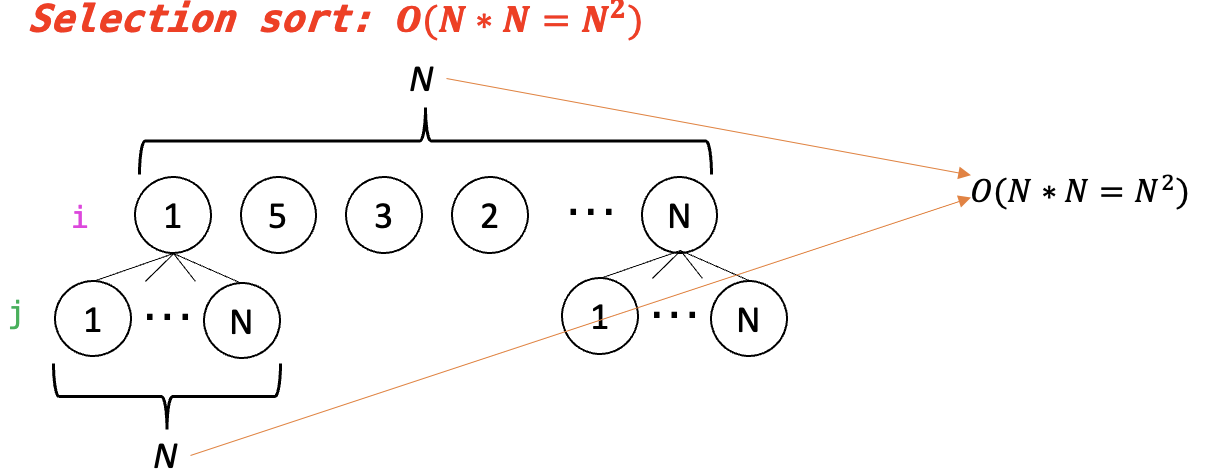
그래프로 생각해보자

• 가장 대표적인 정렬 방법 중 하나인 Selection Sort

def selection_sort(N:int, A:list):
    for i in range(0,N):
        if i == N-1:
            break
        for j in range(i+1,N):
            if A[i] > A[j]:
                temp=A[j]
                A[j]=A[i]
                A[i]=temp

• 

---

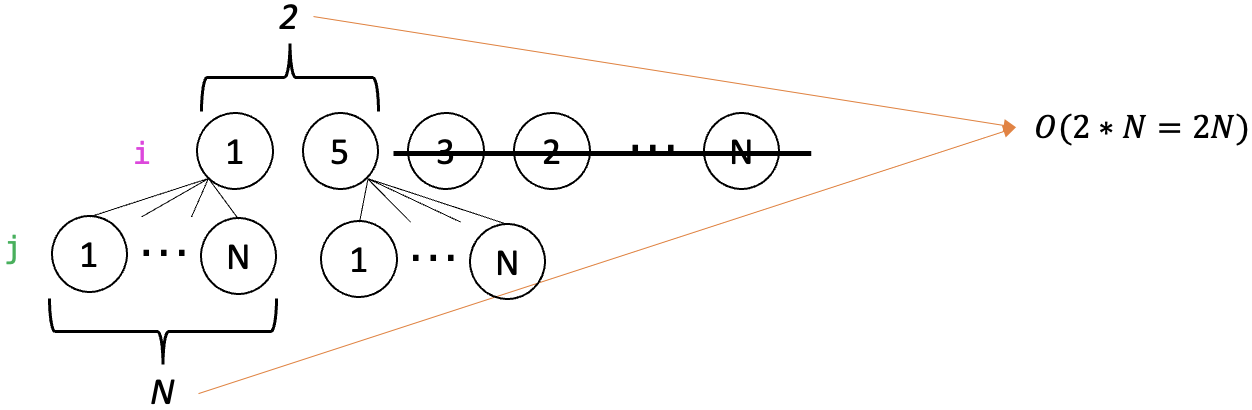
• Selection Sort를 상위 2개만 한다고 가정한다. 이는 ${O(2 * N)}$
  

---

O(N^3)

$O(N^3)$

• 3중 for 문

• 1초 소요 -> 입력(N): 500 $0.5K$개 라고 생각하면 될듯

---

O(2^N)

$O(2^N)$

• 크기가 N인 집합의 부분집합
• 1초 소요 -> 입력(N): $20$개

---

O(N!)

$O(N!)$

• 크기가 N인 순열
• 1초 소요 -> 입력(N): $10$개

---

시간 구하기 연습

1로 만들기 문제

• 매우 유명한 백준 1로 만들기 문제(https://www.acmicpc.net/problem/1463)
  • 시간 제한: 0.15초
  • 입력 갯수: ${1 ≤ N ≤ 10^6}$

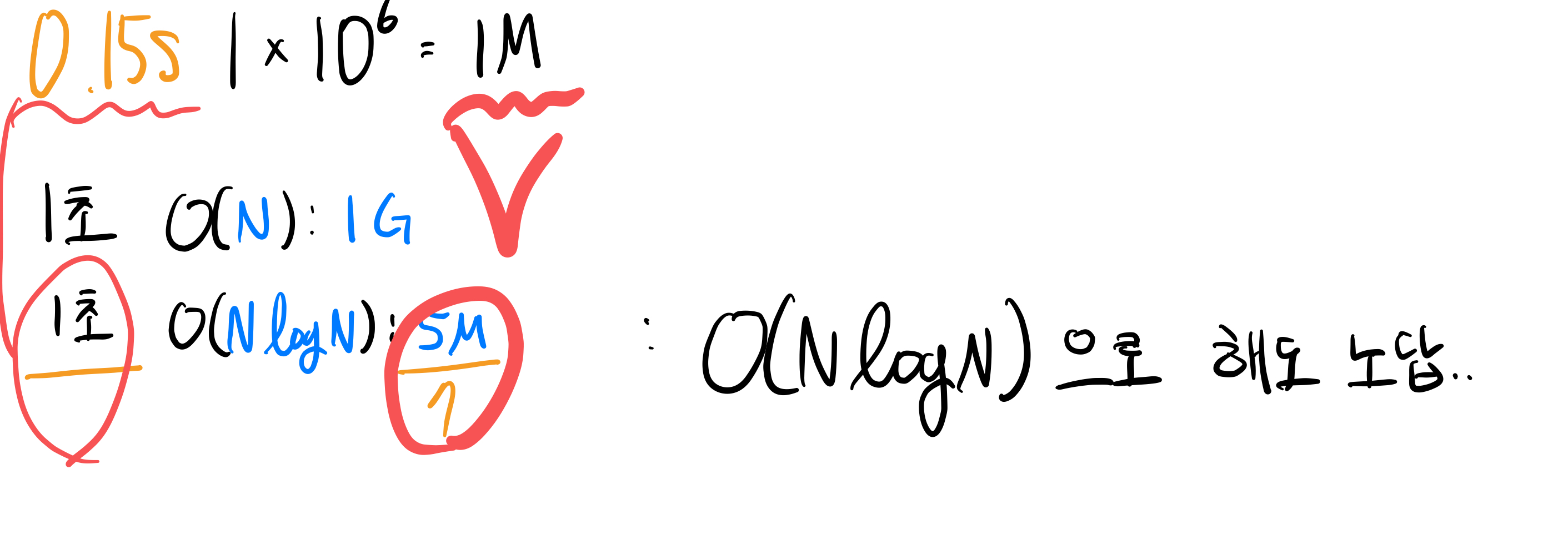
${O(NlogN)}$ 도 답 없기 때문에 for문 하나만 사용하는, len()도 사용하지 않는 ${O(N)}$으로 풀기