문제 푸는 방법

1. 문제 푸는 방법을 글로 정리
2. 정리된 생각을 한 줄씩 코드로 구현
3. 제한 시간 안에 풀리지 않으면 정답 코드 확인

오답 문제 공부 방법

1. 못 푼 문제는 정답 코드를 한 줄씩 글로 번역해보기
2. 번역한 글만보고 다시 코드로 구현하기

파이썬 기초 문법에 대해 잘 모르고
파이썬으로 함수를 어떻게 만드는지 잘 모르시는 분들은
먼저 제 벨로그의 파이썬 왕초보 시리즈와 함수 만들기 글을 보고 풀어보시는 걸 추천드립니다.😉

---

1. 두 수의 나눗셈

✅ 문제 설명

문제 설명

정수 num1과 num2가 매개변수로 주어질 때, num1을 num2로 나눈 값에 1,000을 곱한 후 정수 부분을 return 하도록 soltuion 함수를 완성해주세요.

제한사항

0 < num1 ≤ 100
0 < num2 ≤ 100

입출력 예시

num1	num2	result
3	2	1500
7	3	2333
1	16	62

입출력 예시 설명

• 입출력 예 #1
  num1이 3, num2가 2이므로 3 / 2 = 1.5에 1,000을 곱하면 1500이 됩니다.
• 입출력 예 #2
  num1이 7, num2가 3이므로 7 / 3 = 2.33333...에 1,000을 곱하면 2333.3333.... 이 되며, 정수 부분은 2333입니다.
• 입출력 예 #3
  num1이 1, num2가 16이므로 1 / 16 = 0.0625에 1,000을 곱하면 62.5가 되며, 정수 부분은 62입니다.

✅ 해설

def solution(num1, num2):
    return int(num1 / num2 * 1000)

num1을 num2로 나누고 1000을 곱한다.

---

2. 숫자 비교하기

✅ 문제 설명

문제 설명

정수 num1과 num2가 매개변수로 주어집니다. 두 수가 같으면 1 다르면 -1을 retrun하도록 solution 함수를 완성해주세요.

제한사항

0 ≤ num1 ≤ 10,000
0 ≤ num2 ≤ 10,000

입출력 예시

num1	num2	result
2	3	-1
11	11	1
7	9	-1

입출력 예시 설명

• 입출력 예 #1
  num1이 2이고 num2가 3이므로 다릅니다. 따라서 -1을 return합니다.
• 입출력 예 #2
  num1이 11이고 num2가 11이므로 같습니다. 따라서 1을 return합니다.
• 입출력 예 #3
  num1이 7이고 num2가 99이므로 다릅니다. 따라서 -1을 return합니다.

✅ 해설

def solution(num1, num2):
    return 1 if num1 == num2 else -1

① return 1 → 1이 나오게 해라
② if num 1 == num2 → 만약 num1과 num2가 같다면.
③ else -1 → 다른 경우는(=num1과 num2가 같지 않다면) -1이 나오게 해라

---

3. 분수의 덧셈

✅ 문제 설명

문제 설명

첫 번째 분수의 분자와 분모를 뜻하는 numer1, denom1, 두 번째 분수의 분자와 분모를 뜻하는 numer2, denom2가 매개변수로 주어집니다. 두 분수를 더한 값을 기약 분수로 나타냈을 때 분자와 분모를 순서대로 담은 배열을 return 하도록 solution 함수를 완성해보세요.

제한사항

0 <numer1, denom1, numer2, denom2 < 1,000

입출력 예시

numer1	denom1	numer2	denom2	result
1	2	3	4	[5, 4]
9	2	1	3	[29, 6]

입출력 예시 설명

• 입출력 예 #1
  1 / 2 + 3 / 4 = 5 / 4입니다. 따라서 [5, 4]를 return 합니다.
• 입출력 예 #2
  9 / 2 + 1 / 3 = 29 / 6입니다. 따라서 [29, 6]을 return 합니다.

✅ 해설

갑자기 당황스럽겠지만 천천히 문제를 뜯어보자.
이 방법은 내 생각의 흐름이니, 더 좋은 방법이 있다면 그걸 따라도 된다.

이 문제는
1. 두 분수를 더하고
2. 그걸 기약 분수로 만들고
3. 분자와 분모를 순서대로 나오게 해야 한다.

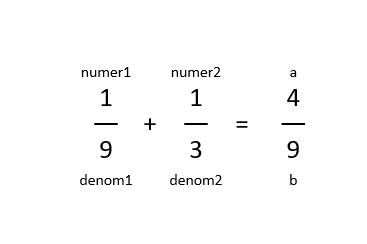
위 그림처럼 나는 return으로 나올 분자와 분모를 각각 a와 b라고 정했다.

분자 구하기

a부터 보자.
위 그림을 보면 a는 5다.
왜 5가 나왔을까?
1×3과 1×2를 더해서 5가 나왔다.
즉, a 는
첫 번째 분자(numer1)에 두 번째 분모(denom2)를 곱하고
두 번째 분자(numer2)에 첫 번째 분모(demon1)를 곱한 후 더한 것이다.
이걸 코드로 쓰면 이렇다.

a = numer1*denom2 + numer2*denom1

분모 구하기

b를 보자.
위 그림을 보면 b는 6이다.
왜 6이 나왔을까?
두 분모끼리 곱해서 6이 나왔다.
즉, b는 첫 번째 분모와 두 번째 분모를 곱한 것이다.
이걸 코드로 쓰면 이렇다.

b = denom1*denom2

최대공약수 구하기

여태 만든 코드를 실행하면 기약 분수로 나오질 않는다.

예를 들어 위 식에서 최종 값은 12/27가 아닌 기약 분수 4/9가 나와야 한다.

어떻게 하면 될까?
여기서 for 반복문을 사용해야 한다.
for 반복문을 모르는 사람들은 내 벨로그의 for 반복문 글을 먼저 보고 오자.

분모와 분자를 서로의 최대공약수로 나누면 기약분수가 된다.
최대공약수는 분모와 분자를 모두 나눌 수 있는 약수 중 가장 큰 수다.
코드를 먼저 보자.

for i in range(min(a, b), 0, -1):
	if a % 1 == 0 and b % i == 0:
    	break

① for i in range(min(a,b), 0, -1)
i는 (a,b) 중 작은 것부터 0전까지(=1까지) 뒤에서부터 하나씩 나오는 것이다.
여기서 a는 12, b는 27이다.
12부터 1까지 하나씩 나온 후 27부터 1까지 하나씩 나오는 게 i다.
그러니까 i는 12, 11, 10, 9, 8, 7, 6,..., 2, 1, 27, 26, 25, 24,...2, 1 이다.

② if a % 1 == 0 and b % i == 0:
만약 a를 1로 나눈 나머지가 0이고 b를 1로 나눈 나머지가 0이라면
그러니까 둘 다 딱 떨어진다면 그게 바로 공약수다.
뒤에서부터 시작했으므로 첫 번째로 나오는 게 제일 큰 공약수, 최대공약수다.

③ break
if조건문을 만족하는 첫 번째 i가 최대공약수기 때문에 나머지는 필요없다.
그래서 최초로 만족하는 하나가 나오면 멈추게끔 break를 걸었다.

이제 최대공약수를 구했으니 이걸로 a와 b를 나누면 된다.

a/i, b/i

이걸 코드로 구현하면 아래와 같다.

def solution(numer1, denom1, numer2, denom2):
    a = numer1*denom2 + numer2*denom1
    b = denom1*denom2
    for i in range(min(a,b), 0, -1):
        if a%i==0 and b%i==0:
            break
    return a/i, b/i

이 문제는 최대공약수를 구하는 방법이 관건이었는데,
사실 내가 만든 코드는 아무런 다른 지식이 없을 때 만드는 코드다.
파이썬 내장함수인 math함수를 사용하면 훨씬 더 쉽고 간단하게 최대공약수를 구할 수 있다.

math.gcd 함수

math.gcd()로 최대공약수를,
math.lcm()으로 최소공배수를 구할 수 있다.

import math
def solution(numer1, denom1, numer2, denom2):
    a = numer1*denom2 + numer2*denom1
    b = denom1*denom2
    return a/math.gcd(a,b), b/math.gcd(a,b)

분자와 분모를 최대공약수로 나누는 것이 똑같지만
math.gcd()를 사용하면 최대공약수를 구하는 코드가 사라지기 때문에 훨씬 간단하고 간편하다.

• 참고
  gcd : greatest common divisor
  lcm : least common multiple

---

4. 배열 두 배 만들기

✅ 문제 설명

문제 설명

정수 배열 numbers가 매개변수로 주어집니다. numbers의 각 원소에 두배한 원소를 가진 배열을 return하도록 solution 함수를 완성해주세요.

제한사항

-10,000 ≤ numbers의 원소 ≤ 10,000
1 ≤ numbers의 길이 ≤ 1,000

입출력 예시

num1	result
[1, 2, 3, 4, 5]	[2, 4, 6, 8, 10]
[1, 2, 100, -99, 1, 2, 3]	[2, 4, 200, -198, 2, 4, 6]

입출력 예시 설명

• 입출력 예 #1
  [1, 2, 3, 4, 5]의 각 원소에 두배를 한 배열 [2, 4, 6, 8, 10]을 return합니다.
• 입출력 예 #2
  [1, 2, 100, -99, 1, 2, 3]의 각 원소에 두배를 한 배열 [2, 4, 200, -198, 2, 4, 6]을 return합니다.

✅ 해설

def solution(numbers):
    return [i*2 for i in numbers]

① i*2
i에 2를 곱한 걸 return해라

② for i in numbers
근데 그 i는 numbers에 있는 원소들이다.

numbers에 있는 원소들을 i라고 정의 한 후
for문이 반복하며 numbers에 있는 원소들을 나오게 하고
그 원소들에 2를 곱한 것이다.