Multivariate Time-series Anomaly Detection via Graph Attention Network (a.k.a MTAD-GAT)

Multivariate Time-series Anomaly Detection via Graph Attention Network
2020 IEEE International Conference on Data Mining (ICDM)

Introduction

이전의 방법들의 한계점 : 시계열 간의 상관관계를 고려하지 않아 False Positive가 탐지 됨

실제 데이터 수집 상황은 multivariate
때문에 univariate time sereis의 이상읕 탐지
하는 것은 해당 시스템의 정상 작동 여부를 판단하기에 어려움이 있음
한 시계열이 변화가 바로 시스템 오류를 의미하지 않을 수 있음
➞ 시스템을 구성하고 있는 각 시계열 간의 상관관계를 확인하는 것이 필요함

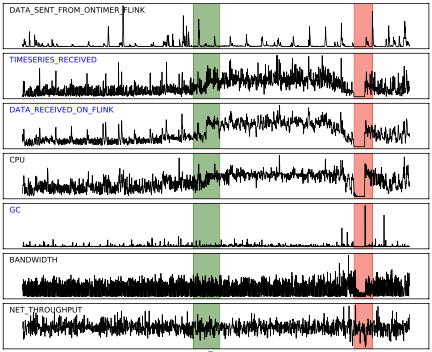
green : noraml / red : abnormal
초록색 영역의 2,3번 시계열 값이 갑작스럽게 증가
→ 이전의 방법들(주로 point-wise)을 사용하면 이상치로 판단할 것
→ 두 시계열의 변화 양상이 유사 : 정상 현상임
→ 시계열 간의 상관관계를 고려했을 때 두 시계열은 정상이며, 시게열 간의 상관관계를 고려하여 이상치를 탐지하는 것이 유의미 함

• EncDec-AD(ICML 2016)
  LSTM Encoder-Decoder, reconstruction error
• telemanom(KDD 2018)
  LSTM based prediction
• OmniAnomaly(KDD 2019)
  stochastic recurrent nerural network, 데이터 분포를 모델링 해서 정상 패턴을 탐지

본 논문에서
1. 다변량 시계열에 존재하는 각 단변량 시계열 간의 상관관계를 포함하는 모델
2. 각 시계열 내의 temporal dependency를 반영하는 모델
을 만족하는 Multivariate Time-series Anomaly Detection via Graph Attention Network(MTAD-GAT)를 제안하고자 함

Methodology

basic structures

1. 2개의 graph layer 사용
   • feature-oriented : 각 시계열 간 인과관계 탐지
   • time-oriendted : temporal dependency 탐지

2. 2개의 모델을 함께 학습

   • forecasting based model
     : focuse on single time stamp prediction

   • reconstruction based model
     : learn a latent representation of the entire time series

다변량 시계열은 단변량 시계열로 형성되어 있음
각 시계열 단위로 이상치를 탐지하는 것을 목표로 함

2개의 graph attention network를 parallel하게 쌓아 inter-feature correlation과 temporal dependency를 모델링
long-term dependency를 해결하기 위해 GRU(Gated Recurrent Unit)를 사용

notation

• $x \in R^{n \times k}$ : multivariate time-series input
• $n$ : num of timestamp(window length)
• $k$ : num of dimensions
• $y \in R^{n}$ : label
  $y_i$는 $i^{th}$ timestamp가 anomaly인지 normal인지 나타냄
• $v_i$ : feature vector of each node

architecture

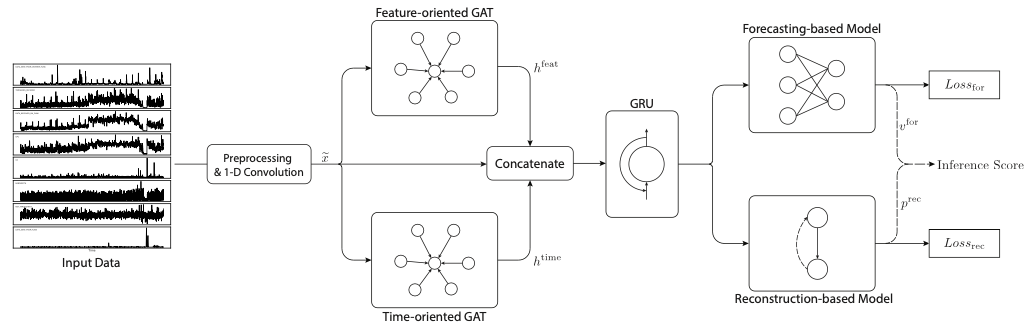
출처 : MTAD-GAT paper

1. Preprocessing & 1-D Convolution

   • normalization(MinMax) → train and test

   • cleaning
     prediction and reconstruction based model은 noise에 민감
     training set에 Spectral Residual 적용하여 이상치가 존재하는 time stamp 주변을 normal value로 대체
     SR-CNN(KDD'19), SR(CVPR'07)
     SR : target의 spectrum에서 average spectrum을 빼면 target의 특징만 남음 → anomaly detection에서는 이상치 부분이 남아 있을 것

     training 과정에서 깔끔한 normal data만 학습하기 위해 cleaning을 진행했을 것으로 생각함

   • feature extraction
     각 시계열은 high-level feature extraction을 위해 1-D convolution 사용
     convolution을 적용하는 것은 time window 내의 local feature 추출에 효과적
     시간 순서 유지 & window 내의 정보를 함께 고려하여 embedding
     

2. Graph Attention
   graph layer → node 간의 relationship을 modeling
   $\left\{v_1, v_2, \cdots, v_n \right\} : node\:set$
   $e_{ij} = LeakyReLU(\omega^{T}\cdot(v_i \bigoplus v_j))$, $\bigoplus : concat$
   attention score $\alpha_{ij} = \frac{\mathrm{exp}(e_{ij})}{\sum^{L}_{l=1}\mathrm{exp}(e_{il})}$, $L$ : node $i$의 adjacent node 수
   GAT output $h_i = \sigma(\sum_{j=1}^{L}\alpha_{ij}v_{j})$, $\sigma$ : activation function(sigmoid)
   
   

   • Feature-oriented GAT
     multivariate time-series의 각 time-series의 상관성에 대한 사전 정보가 없음
     → complete graph(서로 다른 vertex 사이에 한 개 이상의 edge가 존재)를 가정
     각 시계열은 node, 시계열 사이의 relationship은 edg로 표현
     → 모든 시계열이 서로 관련되어 있다고 가정
     feature oriented GAT output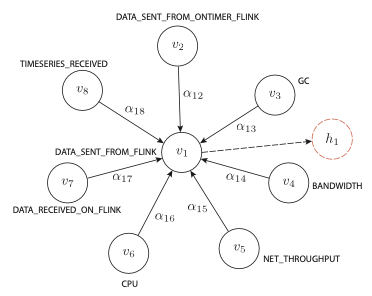 $h^{feat} (k \times n)$

     feature-oriented attention layer
     $h_1$ : final output
     
     

   • Time-oriented GAT
     temporal dependency를 capture하는 목적
     sliding window 내의 timestamps는 complete graph로 가정
     node $x_t$는 timestamp $t$ 시점의 각 dimension의 feature로 표현됨

     
     

   • layer's final output
     feature-oriendted GAT layer: $h^{feat} \: (k \times n)$
     time-oriented GAT layer : $h^{time} \: (n \times k)$
     after preprocessing data : $\tilde{x} \: (n \times k)$
     ⇨ 3개의 output vector를 concat
     $concat\: vectors \: (n \times 3k)$는 GRU의 input으로 사용
     서로 다른 information을 고려하여 학습하기 위함

     
     
   3. Joint Optimization
      본 논문에서는 forecasting and reconstruction models을 함께 사용하여 각 모델 보완
      각 model의 loss를 동시에 업데이트 시키는 것을 목적으로 함
      $Loss= Loss_{for} + Loss_{rec}$

   • forecasting-based model
     three fully-connected layers 사용
     next timestamp의 value를 예측

     $Loss_{for} = \sqrt{\sum_{i=1}^{k}(x_{n,i}-\hat{x}_{n,i})^{2}}$
     
     

   • reconstruction-based model
     VAE를 사용
     latent representation $z$의 주변 데이터 분포 학습을 목표로 함
     time series values를 variable로 취급하여

     시계열 값을 변수로 취급함으로써 VAE 모델은 전체 시계열의 데이터 분포를 캡처할 수 있습니다.

     $Loss_{rec} = E_{q_{\phi}(z|x)}[logp_{\theta}(x|z)]+D_{KL}(q_{\phi}(z|x)||p_{\theta}(z))$

   4. Score
      $Score = \sum_{i=1}^{k}\frac{(\hat{x_{i}}-x_{i})^{2}+\gamma(1-p_{i})}{1+\gamma}$

      $k$ : the number of features\
      $\gamma$ : a hyper-parameter to combine the forecasting-based error and the reconstrution-based probability

Experiments

Datasets

• SMAP (Soil Moisture Active Passice satellite)
• MSL (Mars Science Laboratory rover)
• Original dataset

Setting

• window size $n = 100$
• $\gamma = 0.8$ ; a grid search on the validation set(from 0.4 to 1.0)
• epochs : 100

anomaly or not

보통 각각 point를 신경 쓰기 어렵고, 모든 anomaly point를 탐지하는 것은 어려움이 있음
따라서 아래 그림과 같은 조정된 판단 기준을 사용

• point : 0.5 이상 → anomaly
• adjusted strategy → segment 내에서 anomaly와 인접한 point도 anomaly로 판단

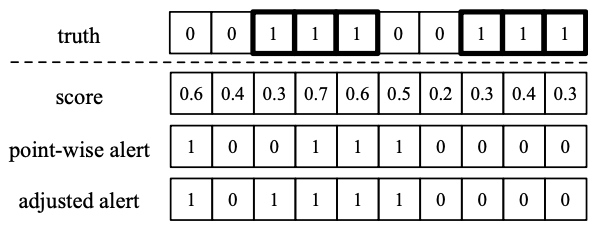
Unsupervised Anomaly Detection via Variational Auto-Encoder for Seasonal KPIs in Web Applications(WWW'18)

Conclusion

• inter and intra time seires relationship
• time seires 간의 관계 파악 → root cause 파악 가능
• feature 간 관계에 대한 사전 지식 없이 실험 → 사전 지식이 포함되면 성능 향상 가능성 존재