[백준] 2133 타일 채우기 C++ (DP)

📌백준 2133 타일 채우기
https://www.acmicpc.net/problem/2133

---

---

• N=1일 때 : 0
  1x2, 2x1 모양 블록으로 3x1 직사각형을 채울 수 있는 방법은 없다.
  d[1] = 0

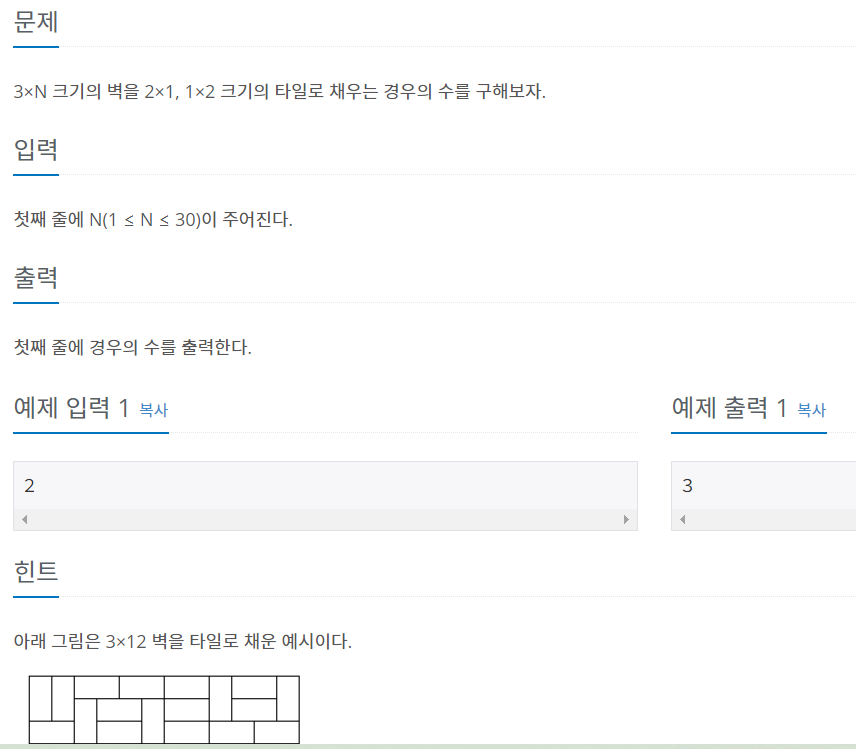
• N=2일 때 : 3
  3가지 방법이 존재한다.
  d[2] = 3
  

• N=3일 때 : 0
  3x1과 마찬가지로 3x3을 채울 방법이 없다.
  d[3] = 0

• N=4일 때 :
  2x2, 2x2의 경우로 나누어 생각해볼 수 있다.
  
  이렇게 하면 (N=2 일 때 방법수) x (N=2 일 때 방법수) 해주면 되겠네!
  d[2] x d[2] = 9
  하지만 이게 끝이 아니다. 함정이 숨어있었다.
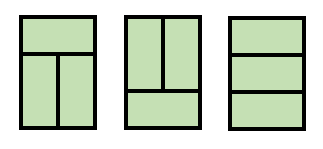
  N=4일 때만 가지는 고유의 모양이 있었던 것이다
  
  바로 이 두가지이다.
  그래서 +2까지 해줘야한다.
  d[4] = d[2] x d[2]+2 = 11

• N=5일 때 : 0
  마찬가지로 3x5일 때 방법의 수는 0이다. N이 홀수면 0인가보다.
  d[3] = 0

• N=6일 때 :
  N=4에서 한 것 처럼 나눠서 생각해보자.
  
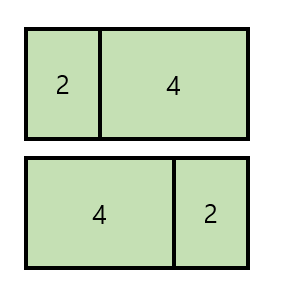
  나누면 위와 같다. 2x4, 4x2일 때로 나눠진다. 1x5, 3x3은 왜 없느냐?
  홀수일 때는 방법이 없기 때문에 제외하고 생각하기로 했다.
  2x4일 때) 마찬가지로 d[2] x d[4]해주면 되겠구나!
  4x2일 때) 마찬가지로 d[2] x d[4]해주면 ㄷㅚ지않는다.
  왜냐? 중복이 존재하기 때문.
  왠만한 모양은 다 겹칠 것이다. 근데 N=4일 때는 고유의 모양을 가진다고 했다.
  그럼 4x2일 때 4가 고유의 모양일 때만 생각해주면 중복을 피할 수 있겠구나!
  이 때 방법 수는 d[2] x 2가 된다.
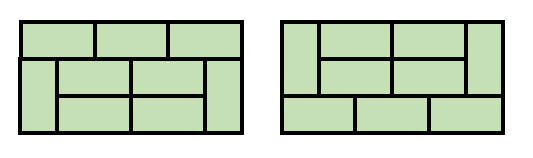
  d[6] = d[2] x d[4] + d[2]x2 인데, N=6일 때도 고유의 모양 2개를 가진다.
  따라서
  d[6] = d[2] x d[4] + d[2] x 2 + 2 = 41
  

• N=8일 때까지만 구해보자.
  2x6, 6x2, 4x4로 나눌 수 있다.
  
  2x6일때) d[2] x d[6] 하면 되겠구나!
  6x2일때) 6의 고유 모양 2 x d[2] 하면 되겠군아
  4x4일때) d[4] x d[4] ?? 이것도 d[2] x d[6]과 중복될 것 같다. (d[2]로 돌려넣기니까) d[4]에는 고유의 모양도 다 포함되어 있는 방법수이니 d[4] x 4의 고유 모양 2로 구하자. => d[4] x 2
  d[8] = d[2] x d[6] + d[2] x 2 + d[4] x 2 + 2 = 153

N	1	2	3	4	5	6	7	8
방법수	0	3	0	11	0	41	0	153

이제 규칙을 찾아 점화식을 찾으러 가보자.

d[4] = d[2] x d[2] +2
d[6] = d[4] x d[2] + d[2] x 2 + 2 = 41
d[8] = d[6] x d[2] + d[4] x 2 + d[2] x 2 + 2 = 153

d[N] = d[N-2] x d[2] + d[N-4] x 2 + d[N-6] x 2 + ... + 2
(* d[0] = 0을 임의로 설정해줌)

---

#include <iostream>
using namespace std;

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);

    int N;
    cin >> N;

    int d[31];
    d[0] = 1;
    d[1] = 0;
    d[2] = 3;

    for (int n = 3; n <= N; n++)
    {
        if (n % 2 != 0) d[n] = 0;
        else
        {
            for (int i = 2; i <= N; i += 2)
            {
                if (i == 2) d[n] = d[n - i] * d[2];
                else if((n-i) >= 0) d[n] += d[n - i] * 2;
            }
        }
    }
    cout <<d[N];
}