탐색
이진탐색
- 정렬되어 있는 배열이라는 전제 조건이 있음
- 원하는 값(x)을 찾을 때, 배열의 가운데 값(m)을 기준으로 크고 작음을 비교해 탐색하는 것
- m이 x보다 크면, 배열의 오른쪽을 뚝 잘라 왼쪽에서 다시 가운데 값을 정의(m1)하고 비교, 반복
- 탐색하는 배열이 반씩 줄어들기 때문에 시간복잡도 측면에서 유리
완전탐색
- 가능한 모든 경우의 수를 다 구해서 값을 찾는 것
- 결과 값이 가장 확실하지만 그만큼 시간이 가장 오래 걸림
- 알고리즘에서 for, if를 사용해 찾는 것이 보통 완전 탐색 방법
탐욕(greedy)알고리즘
- 최적해를 찾는
근사적방법 - 그 순간에 최적이라고 생각되는 것을 선택해 최종적인 해에 도달
- 전역적으로 최적이라는 보장은 없지만 지역적으로 최적
DFS, BFS(깊이,너비우선탐색)
- 둘 다 모든 경우에 대해 탐색하기 때문에 맹목적인 탐색 기법
- DFS는 다음 레벨로 이동하면서 탐색하고, 못 찾으면 백트래킹을 해야 하기 때문에 현재 노드의 위치를 스택에 저장해야 함
- BFS는 같은 레벨에 대한 탐색을 모두 마치고 다음 레벨로 이동. 다음 레벨의 노드를 모두 큐에 넣고 순서대로 탐색함
최단거리(다익스트라)
동적계획법
정렬
힙정렬
- 힙을 이용해 최대, 최소값을 찾는 정렬 방법
- 힙: 1) 완전이진트리 기반 2) partial order 만족
- 최대값을 구할 경우, 배열을 최대힙으로 만들어주면 루트 노드는 가장 큰 값을 갖게 된다.
- 배열의 마지막 값과 루트노드와 바꿔주고 업데이트된 루트노드를 다운힙(아래로 내리면서 정렬) 진행
- 결국 루트로 최대값이 올라올 수밖에 없고, 가장 큰 것으로 확인된 요소는 배열에서 없다고 가정하면서 정렬을 진행하게 됨. 최소값은 최소힙으로 만들면 됨
완전이진트리 사용 장점
left 완전 이진트리이기 때문에 인덱스로 부모, 자식 노드에 바로 접근 가능
선택정렬
- 배열의 첫 번째 위치에서 시작해 나열된 값 중 최소값을 구해 앞으로 이동
- 그 다음 두 번째 위치에서 시작해 오른쪽 값들 중 최소값을 앞으로 이동
- 위 과정을 배열의 길이 n까지 계속 반복하면서 마지막 값까지 진행하면 정렬 완료
- 배열의 길이가 작으면 속도가 빠르지만, 길이가 길 수록 속도가 급격히 하락
버블정렬
- 배열의 첫번째 위치에서 인접한(바로 옆의)값과 비교해 큰 값을 오른쪽으로 이동
- n-1번째까지 한바퀴를 돌게 되면 최대값은 배열의 맨 마지막으로 가게 되어있음
- 그 다음 배열의 첫번째에서 n-2까지 비교, 인덱스를 줄여가면서 비교해 정렬
삽입정렬
- 배열이 어느정도 정렬된 상태에서 사용한다.
- 정렬이 되어있지 않은 배열의 모든 요소를 정렬된 배열과 비교하여, 들어갈 위치를 찾고 그 위치에 삽입한다.
- 정렬이 필요할 때만 연산하기 때문에 빠르다
합병(병합)정렬
- 분할정복(Divide and Conquer) 알고리즘의 일종
- 배열의 가장 최소단위가 1이 될 때까지 분할하고, 다시 합치면서 값을 비교하며 정렬함
- 분할하면서 추가적 배열이 필요하게 되고, 메모리가 소요되어 공간복잡도 효율은 떨어짐
- 합칠 때 이미 자기 자신은 정렬이 되어있기 때문에, 앞의 값을 기준으로 분리되어 있는 다른 값끼리만 비교하면 됨
- ex) [6,7][5,8] 을 비교하면 이미 배열 안은 정렬되어있으므로 6과 5,8만 비교하면 최소값 바로 확인 가능
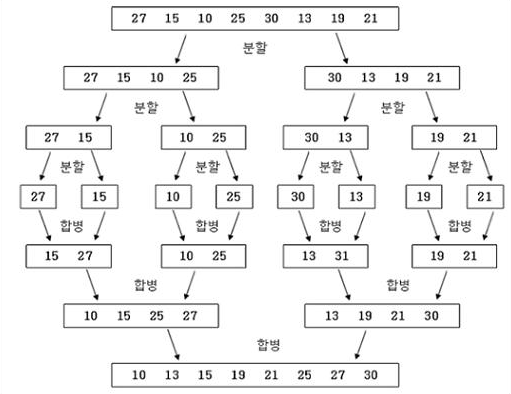
분할정복 알고리즘
문제를 나눌 수 없을 때까지 나눈 다음, 나누어진 각각의 문제들을 풀면서 다시 합병을 하여 문제의 답을 얻는 알고리즘이다.
퀵정렬
셸정렬
그 외
시간복잡도 관련 정리가 잘 되어 있는 링크 발견!