수학의 정석을 처음 펼쳤을 때 배웠던 것이 행렬이었던 것 같은데, 다시 배우니까 뭔가 감회가 새롭다 🥺 벡터, 스칼라 등 처음 들은 단어가 있긴 하지만 개념 자체는 쉬운 단원이었다. 2주차부터 툴 쓴다고 하니 얼른 넘어가야겠다 기대기대

1. matrices and vectors

행렬matrix

2차원 배열(2-dimensional arrays). 데이터를 organize, index 하기 위해서 사용된다. 대문자는 행렬로, 소문자는 일반적인 숫자/자료값/스칼라값/벡터를 지칭한다. (by convention, not always true)

그나저나 matrix의 복수형은 matrices다. 이런 복수형 변화는 처음 봐서 좀 신기 🙄

• A matrix is a rectangular array of numbers written between square brackets.
• Rectangular array of numbers
• "Scalar" means that an object is a single value, not a vector or matrix.

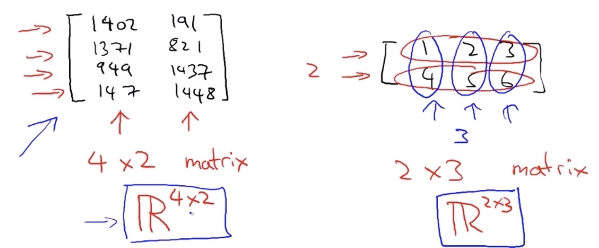
벡터vector

특수한 형태의 배열. 하나의 열만 가지는 nx1(one column and many rows) matrix. n개의 원소를 지닌 벡터를 n-dimentinal vector라고 부른다.

vectors are a subset of matrices.

?-indexed

index가 1부터 시작하는지, 0부터 시작하는지에 따라 1-indexed 또는 0-indexed라고 한다. 프로그램이 언어에 따라 배열의 시작이 0인지, 1인지 다르기 때문에 붙여진 것으로 보인다.

수학에서는 1-indexed를, 기계 학습에서는 0-indexed를 주로 사용한다.

읽기 자료

읽기 자료에서 처음으로 Octave/Matlab의 command를 실행할 수 있는게 있어서 해봤는데 짱 신기하다. 아래 코드를 실행하면 이미지처럼 나온다.

• 세미 콜론이 줄 바꿈처럼 사용됨
• 배열의 사이즈를 구할 수 있음
• dim_A랑 dim_v는 이해가 안 감\

% The ; denotes we are going back to a new row.
A = [1, 2, 3; 4, 5, 6; 7, 8, 9; 10, 11, 12]

% Initialize a vector 
v = [1;2;3] 

% Get the dimension of the matrix A where m = rows and n = columns
[m,n] = size(A)

% You could also store it this way
dim_A = size(A)

% Get the dimension of the vector v 
dim_v = size(v)

% Now let's index into the 2nd row 3rd column of matrix A
A_23 = A(2,3)

2. 연산

행렬들을 더하고 빼는 것과, 곱하는 것은 linear algebra의 주요 연산자라는 점을 기억하고, 간단한 방법에 대해 알아보자.

더하기,빼기

배열, 벡터끼리 사칙연산을 하거나 스칼라연산(행렬이나 벡터에 실수를 연산하는)을 할 수 있다. 해당 챕터의 핵심은 같은 차원의 배열끼리만 계산할 수 있다는 것이다. 스칼라는 number의 fancy version이라고 했는데 ㅋㅋ 그냥 실수라고 보면 된다. 하지만 계산을 할 때는 스칼라곱이라고 이름을 붙여준다.

행렬x벡터

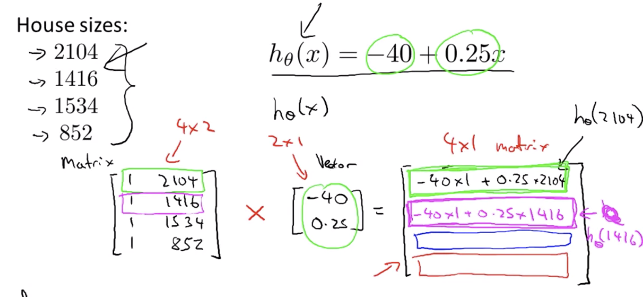
mxn matrix A와 nx1 vector x를 곱했을 때 결과는, m-dimensional vector가 된다. A의 첫번째 행과 x의 모든 값을 각각 곱한 뒤 더해주면 결과의 첫 번째 element가 나온다.

왜 행렬간의 곱을 보여주는지 봤더니, 만약 머신러닝 알고리즘이 만든 함수 h가 1차 함수라면, 값들을 모두 넣어서 결과값을 계산해야 하는데 이때 상수 열은 1로, 변수 열에는 해당 값들을 넣어서 곱해주면 예측 결과값을 가진 벡터값이 나오게 된다.

따라서 행렬벡터의 곱을 도출하는 코드를 작성하면 예측 가능하게 되는 것이다. 강의에서는 코드를 쓰는 것보다 배열로 만드는게 더 computationally efficient(?)하다고 말한다.

prediction = DataMatrix x parameters

행렬x행렬

m x n matrix A, n x o matrix B를 곱할 때는 우선 A의 열과 B의 행이 같아야 한다. 그리고 결과 행렬은 m x o matrix가 된다.

예시를 들어주는 것을 보면 두 번째 행렬을 벡터 단위로 나누어서 곱해주는 것을 볼 수 있다. 가설 함수 h가 만약 여러 개일 경우를 예시로 들어보면 왜 벡터처럼 취급하는지 알 수 있다.

위의 행렬x벡터를 곱한 것처럼 parameter vector들을 오른 쪽으로 계속 추가해서 결과 값을 보면, 가설 함수에 따른 예상 결과값들을 받아볼 수 있다. (첫 번째 열은 가설 함수 1의 결과 등)

행렬 곱을 진행하기 위한 linear algebra 라이브러리가 많이 있고, 행렬 곱을 계산하는 것에 최적화되어 있다고 한다. 인기 많은 상위 10개 컴퓨터 언어들은 대부분 있다고 함!

3.Matrix Multiplication Properties

교환 법칙

스칼라 곱에서는 3x5나 5x3이 같지만, 행렬 곱에서는 성립하지 않는다. 하지만 A가 항등 행렬일 경우에는 성립한다.

결합 법칙

곱할 때 앞에 것을 먼저 하든, 뒤에 것을 먼저 하든 결과는 같다. 3x(5x2) = (3x5)x2

identity matrix

항등 행렬이라고 부르며, 정사각 배열이고 대각선 요소들이 1, 나머지 요소는 0이다. 항등 행렬의 경우 I로 표시하며, I와 곱할 수 있는 행렬 A가 있다고 가정할 때 AI = IA = A이다.

4. Inverse and Transpose

역행렬Inverse

결과를 1로 만들어주는 역수가 있뜻, 행렬에서도 결과 I(항등 행렬)를 가져다주는 역행렬이 있다.

• 정방 행렬만 역행렬을 가질 수 있다.
• 0으로만 이루어진 행렬은 역행렬을 자리 수 없다. (=singular matrix = degenerate matrix)

역행렬을 찾아주는 오픈 소스 라이버리도 많다. 넘나 신기하네 🤔

전치행렬Transpose

임의의 행렬 A dimension이 reversed된 행렬을 말한다.