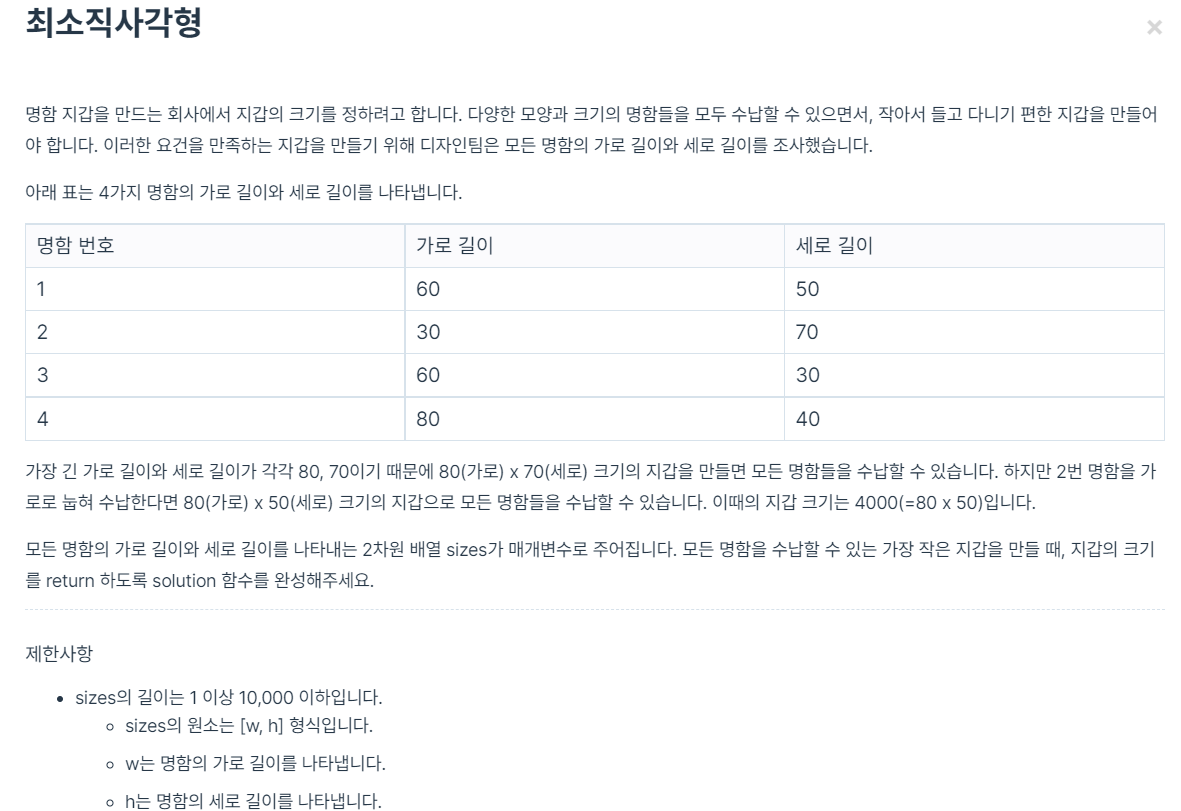
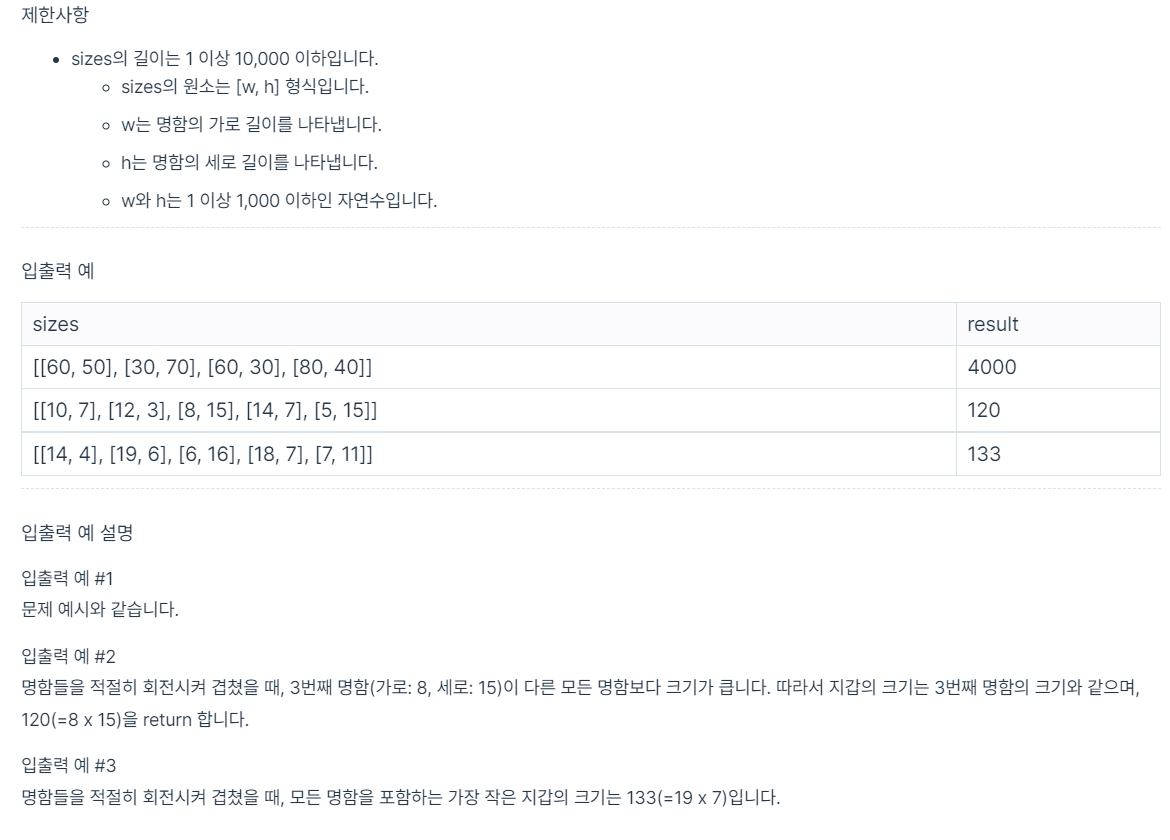
문제
나의 풀이
function solution(sizes) {
let i1=[];
let i2=[];
for(i=0; i<sizes.length; i++){
sizes[i].sort((a,b)=> a-b)
i1.push(sizes[i][0])
i2.push(sizes[i][1])
}
return Math.max(...i1)*Math.max(...i2)
}
명함을 세로가 길게 이리저리 돌려 정리하는 상상을 해보고 아이디어를 얻었다.
1. 명함 정리
sizes 배열의 원소배열을 오름차순으로 정리한다. 그렇게 하면 [가로a,가로b] 는 항상 a<b가 된다.
2. 지갑 사이즈 정하기
가로a중에서 가장 긴 길이(최대값)와 세로b중에서 가장 긴 길이(최대값)를 뽑는다. 그렇게 하면 모든 명함을 (이리저리 돌려서) 넣을 수 있는 최소 크기의 지갑 사이즈가 된다.
넘의 풀이

function solution(sizes) {
const [hor, ver] = sizes.reduce(([h, v], [a, b]) => [Math.max(h, Math.max(a, b)), Math.max(v, Math.min(a, b))], [0, 0])
return hor * ver;
}이렇게 기가 막히게 줄이다니 ㄷㄷ
reduce의 acc 누적값을 더하는것만 해서 max를 썼을 때 누적값은 max중의 max라는 점이 신선하다.
그래도 Math.min을 왜 쓴건지 모르겠는데..?
알겠다!
const [hor, ver]
// 최소지갑의 가로, 세로를 구하는데
= sizes.reduce(([h, v], [a, b]) =>
// sizes배열의 원소 누적값-acc([h, v])와 현재값-cur([a, b])
[Math.max(h, Math.max(a, b)), Math.max(v, Math.min(a, b))],
// Math.max(a, b) 현재값 중 큰값/ Math.min(a, b) 현재값 중 작은 값
// 초기값이 [0,0]이니까 현재값a,b를 결정한 직후 모습은 (현재값이 [7,15]라면)
// [Math.max(0, 15), Math.max(0, 7)]이 되고
// 누적 [h,v]는 h에는 누적 최대값 중에서 최대값이,
// __ __ __ __ __ v에는 누적 최소값 중에서 최대값이(이게 킬포!)뽑히는거시다~
[0, 0])
// 초기값 (노상관)
[Math.max(h, Math.max(a, b)), Math.max(v, Math.min(a, b))],
// Math.max(a, b) 현재값 중 큰값/ Math.min(a, b) 현재값 중 작은 값
// 결과적으로 위 부분은 sort((a,b)=> b-a) 내림차순 역할을 하는것.
그으러쿠우나~

