문제
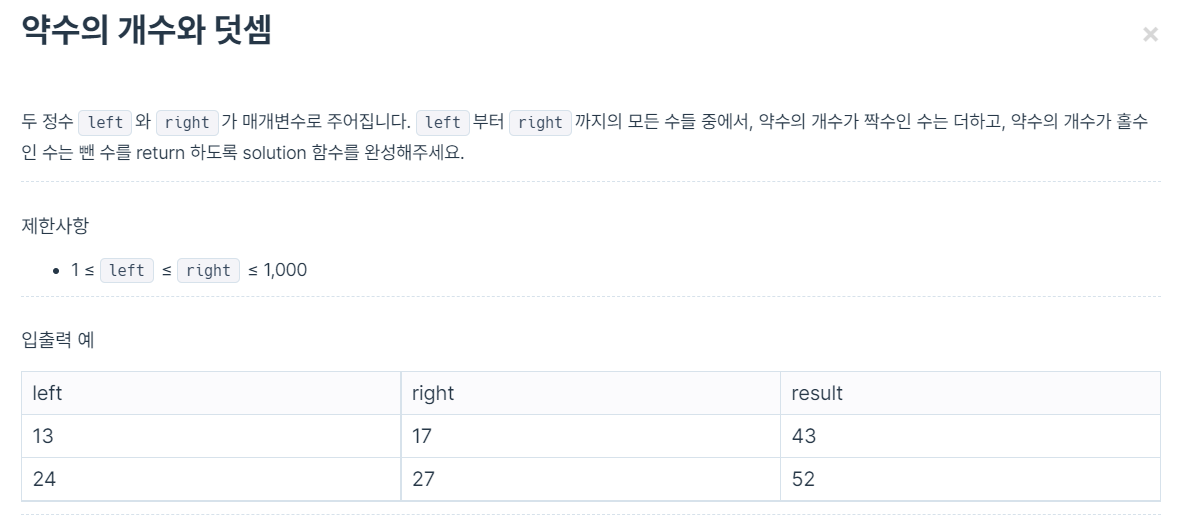
나의 풀이

Math.sqrt()
제곱근 구해주는 함수
완전 제곱수일 경우에만 약수의 갯수가 홀수가 되므로
완전제곱수의 제곱근을 구해서 정수이면 더하고 정수가 아니면 빼도록 했다.
정수여부는 1로 나눈 나머지가 0일 경우로 했다.
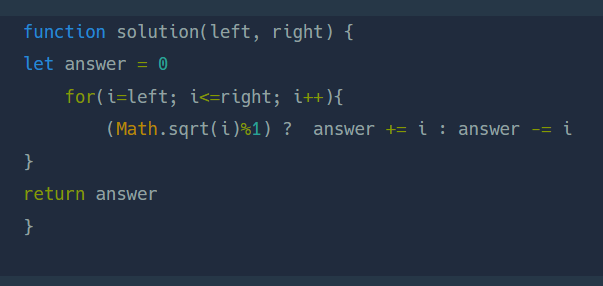
넘의 풀이1
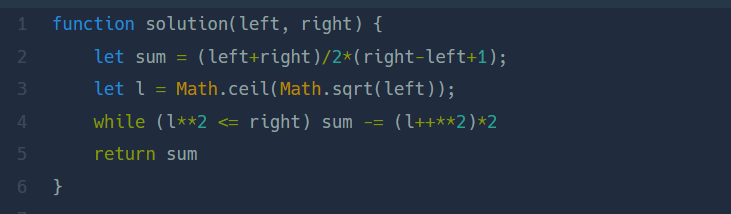
무슨 코드인지 생각해보자
left트 부터 right까지 다 더하고 완전 제곱수인 수는 2배하여 뺐다(고 코드 작성자가 댓글 달아놔서 알수있었음)
**곱셈연산을 두번 쓰면 제곱이 되는구나!
Math.ceil()
소수점 이하를 올림하는 함수
.floor() 소수점이하 버림
.round() 소수점이하 반올림
let l = Math.ceil(Math.sqrt(left));l을 left의 제곱근을 구해 소수점이하를 올림 한 수로 선언하고
while (l**2 <= right) sum -= (l++**2)*2l을 하나씩 늘려 가며서 right 보다 작아질 때 까지 총합에서 빼주었다.
예를 들어 범위가 13부터 17 까지라면
13의 제곱근은 3과 4사이의 수이다.
그럼 올림하면 4가되니까 4를 제곱하면 13과 17 사이에 있는 완전 제곱수 16이 된다.
만약 범위가 13부터 15까지라면 완전제곱수가 right인 15보다 작아지니까 빼지 않게 된다
오 이렇게도 푸는구나!
넘의 풀이2
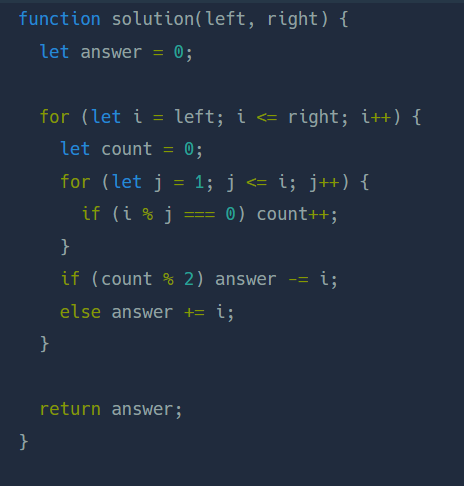
- 약수의 갯수를 구해서 (가장 안쪽 if문)
- 약수의 갯수가 짝수인지 구함 (두번째 if문)
처음에 약수의 갯수를 구하는 풀이로 갈까 하다가 너무 복잡할 것 같아서 다른 방법으로 했는데
이렇게 쓰는거구만!
넘의 풀이3
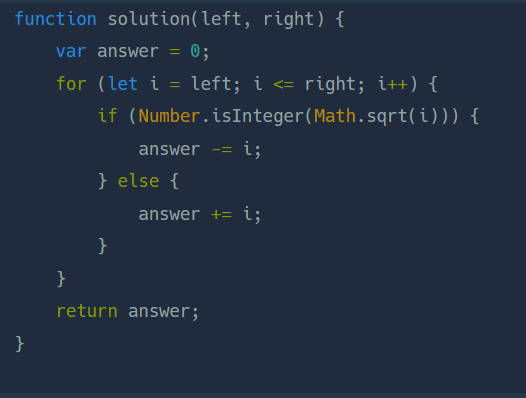
나와 같은 풀이
