Brute Force
brute: 무식한, force: 힘 => 무식한 힘으로 해석
완전탐색 알고리즘. 즉, 가능한 모든 경우의 수를 탐색하면서 요구조건에 충족되는 결과만을 가져온다. 이 알고리즘의 강력한 점은 예외 없이 100%의 확률로 정답만을 출력한다.
-
일반적 방법으로 문제를 해결하기 위해서는 모든 자료를 탐색해야 하기 때문에 특정한 구조를 전체적으로 탐색할 수 있는 방법을 필요로 한다.
-
알고리즘 설계의 가장 기본적인 접근 방법은 해가 존재할 것으로 예상되는 모든 영역을 전체 탐색하는 방법이다.
-
선형 구조를 전체적으로 탐색하는 순차탐색, 비선형 구조를 전체적으로 탐색하는 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS) 이 가장 기본적이다.
예시) '1부터 100까지의 합을 구하라' 라는 문제에서 정말 '1부터 100까지 모두 직접 더한다' 라는 풀이가 브루트 포스의 예시 가 된다.
이처럼 브루트포스는 매우 간단한 방법이지만 숫자가 커지면서 문제가 발생한다. 위의 예제를 1부터 1000억까지 더한다면 일반적으로 컴퓨터는 1초에 약 1억 번에 연산이 가능하므로 1000초 즉,
약 17분이 소요된다. 단순히 더하기 문제인데도 말이다.
이처럼 브루트포스 알고리즘은 시간 측면에서 매우 비효율적 이다.
순차 탐색
- 주어진 문제를 구조화 한다.
- 구조화된 공간을 적절한 방법으로 해를 찾을 때 까지 탐색한다.
너비 우선 탐색 (BFS,Breadth-Fist Search)
-
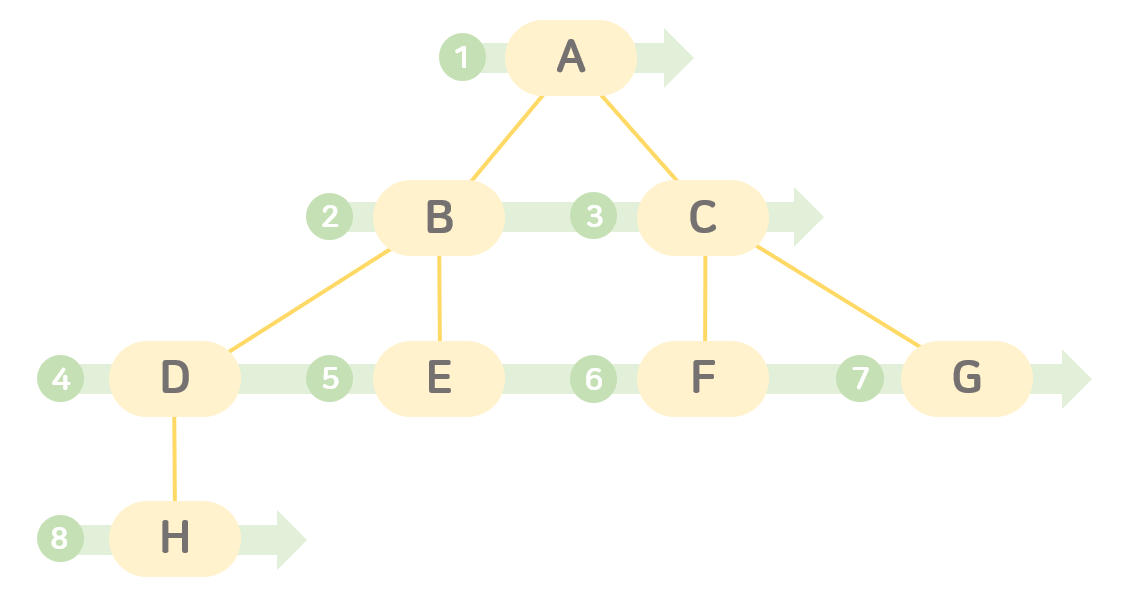
탐색 트리의 루트노드부터 목표노드까지 단계별로 횡방향으로 탐색하는 방식
-
두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 선택
-
시작 노드에서부터 거리에 따라 단계별로 탐색하며, 재귀적으로 동작하지 않는다.
-
그래프 탐색 시 어떤 노드를 방문했었는지 여부를 검사해야 한다. 이를 검사하지 않을 경우 무한루프에 빠질 수 있다.
구현 방법
- 큐(Queue)를 이용: 선입선출(FIFO) 원칙으로 방문한 노드들을 차례대로 큐에 저장한 후 꺼낸다.
public static void bfs(int i) {
Queue<Integer> q = new LinkedList<>();
q.offer(i);
visit[i] = true;
while(!q.isEmpty()) {
int temp = q.poll();
System.out.print(temp + " ");
for(int j=1; j<n+1; j++) {
if(map[temp][j] == 1 && visit[j] == false) {
q.offer(j);
visit[j] = true;
}
}
}
}
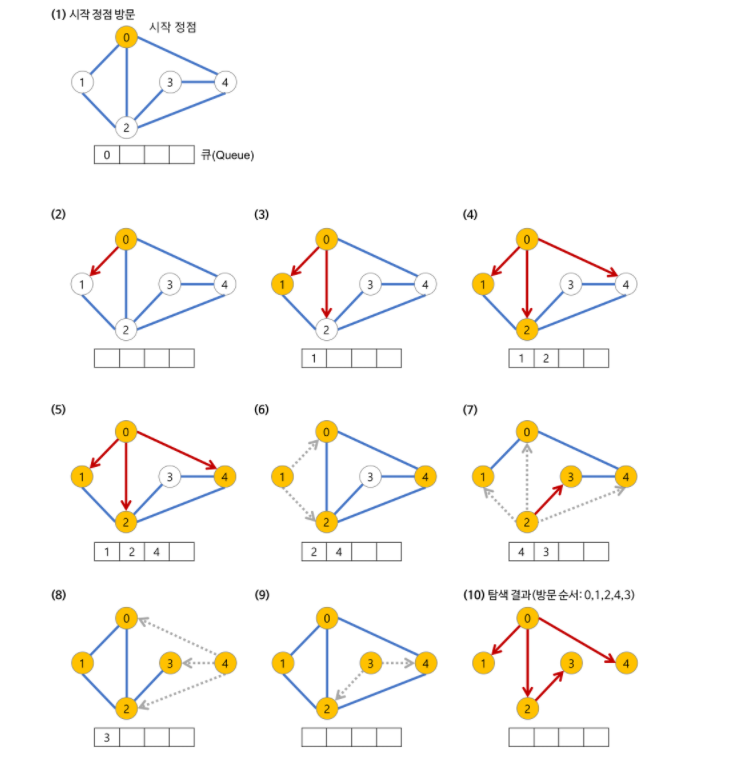
출처: https://bbangson.tistory.com/42 [뺑슨 개발 블로그]
장점
- 출발노드에서 목표노드까지 최단 길이 경로를 보장한다.
단점
- 경로가 매우 길 경우 탐색 가지의 증가에 따라 비교적 많은 기억 공간을 필요로 한다.
깊이 우선 탐색 (DFS,Depth-First Search)
-
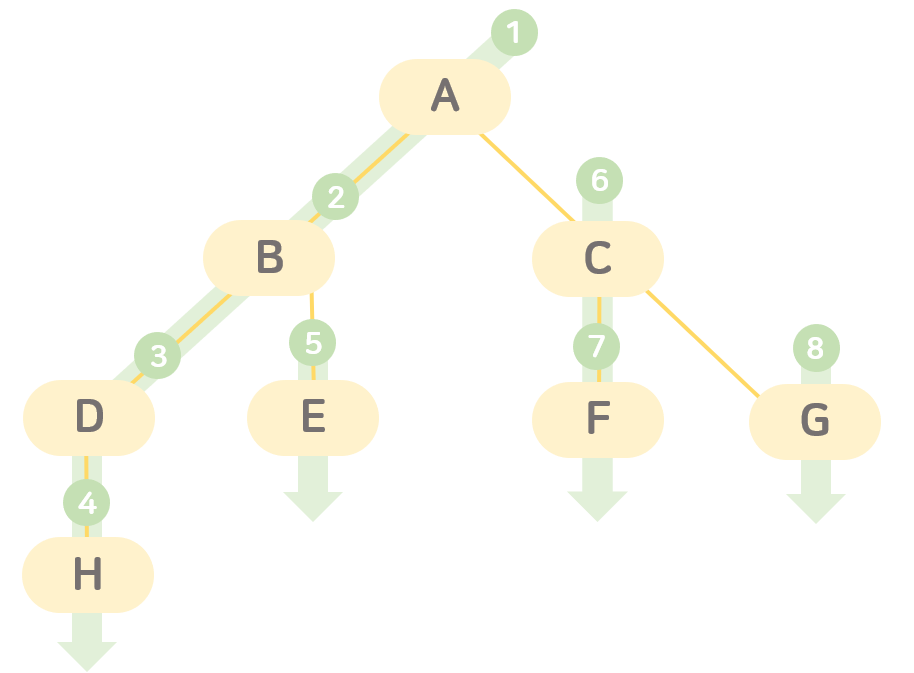
루트 노드(혹은 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
-
모든 노드를 방문하고자 하는 경우에 선택한다.
-
자기 자신을 호출하는 순환 알고리즘의 형태를 가지고 있다.
-
그래프 탐색 시 어떤 노드를 방문했었는지 여부를 검사해야 한다는 것이다. 이를 검사하지 않을 경우 무한루프에 빠질 수 있다.
구현 방법
-
순환 호출 이용
-
명시적인 스택(Stack) 사용 : 방문한 정점들을 명시적 스택에 저장하였다가 다시 꺼내어 작업한다.
// dfs, 재귀, 인접 행렬, i 정점부터 시작한다.
public static void dfs(int i) {
visit[i] = true;
System.out.print(i + " ");
for(int j=1; j<n+1; j++) {
if(map[i][j] == 1 && visit[j] == false) {
dfs(j);
}
}
}
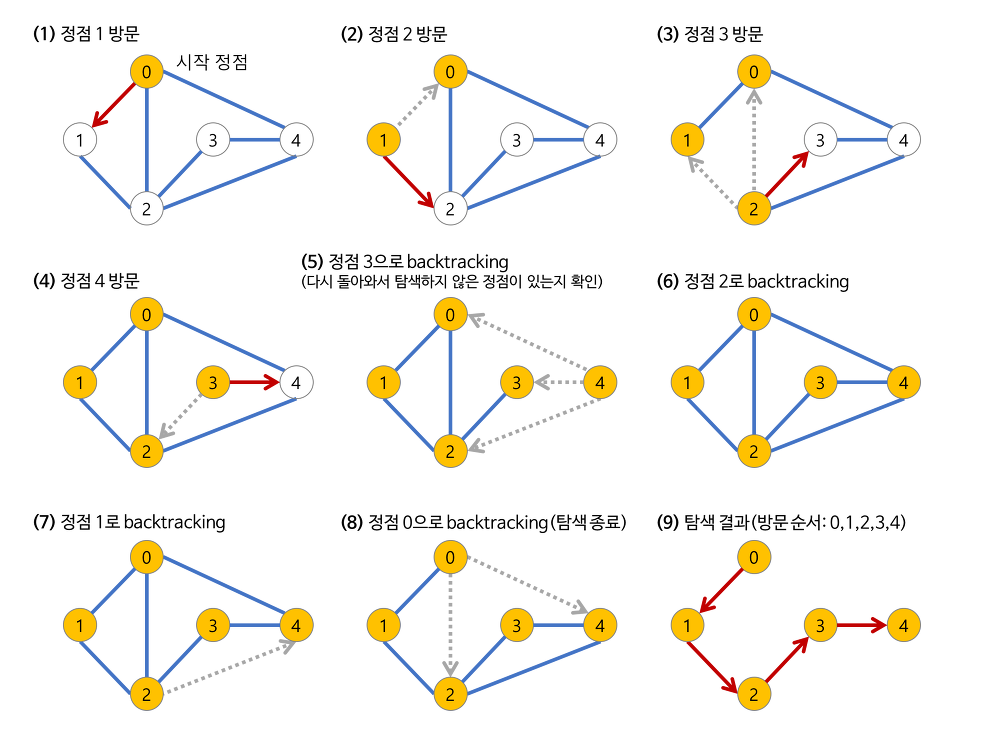
출처: https://bbangson.tistory.com/42 [뺑슨 개발 블로그]
장점
-
현 경로상의 노드들만 기억하면 되기 때문에 저장공간의 수요가 비교적 적다.
-
목표노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있다.
단점
-
해가 없는 경로 속에 깊이 빠질 수 있다. 따라서 실제 경우에는 미리 정한 임의의 깊이까지 탐색하고 다음의 경로를 탐색하는 방법이 유용할 것이다.
-
얻어진 해가 최단 경로라는 보장이 없다. 해에 다다르면 탐색을 끝내므로, 목표에 이르는 경로가 다수인 문제에 대해 깊이 우선 탐색은 얻어진 해가 최적이 아닐 수 있다.
-
BFS에 비해 좀 더 간단하지만 느리다.
DFS vs BFS
| DFS | BFS | |
|---|---|---|
| 동작 원리 | 스택 | 큐 |
| 구현 방법 | 재귀 함수 이용 | 큐 자료구조 이용 |
(bonus) 비트마스킹
사용하는 이유
- DP나 순열 등, 배열 활용만으로 해결할 수 없는 문제
- 작은 메모리와 빠른 수행시간으로 해결 가능(But,원소의 수가 적어야한다.)
- 집합을 배열의 인덱스로 표현 가능
- 코드가 간결해짐
비트마스킹 활용해보기
- 0과 1로 flag 활용
[1,2,3,4,5] 라는 집합이 있다고 가정하자.
여기서 임의로 몇개를 골라 뽑아서 황긴을 해야한다 (즉, 부분집합)
[1,2,3,4,5] -> 11111
[2,3,4,5] -> 11110
[1,2,5] -> 10011
[2] -> 00010위처럼 각 요소를 인덱스처럼 표현하여 효율적인 접근이 가능하다.
집합에 i번째 요소가 존재하면 1, 존재하지 않으면 0을 의미한다.
여기서, 해당 부분집합에 i를 추가하고 싶을 때 i번째 비트를 1로만 바꿔주면 되는데 이런 행위를
비트 연산 을 통해 가능하다.
비트 연산
| 연산자 | 설명 |
|---|---|
| & (and) | 둘 다 1이면 1 |
| | (or) | 둘 중 1개만 1이면 1 |
| ~ (not) | 1이면 0, 0이면 1 |
| ^ (xor) | 둘의 관계가 다르면 1, 같으면 0 |
| <<, >> (shift) | A<<B라면 A를 좌측으로 B비트만큼 미는 것 |
- 삽입
만약 이진수로 10101로 되어 있을 때 i번째 비트 값을 1로 변경하려고 한다.
i=3일 때 변경후에는 11101이 나와야 한다. 이런 경우 OR연산을 활용한다.
10101 | 1 <<31<<3 은 1000이므로 10101 | 01000이 되어 11101이 된다.
- 삭제
반대로 0으로 변경하려면, AND연산과 NOT을 활용한다.
11101 & ~1 <<3~1<<3 은 10111이므로, 11101 & 10111이 되어 10101을 만들 수 있다.
- 조회
i번째 비트가 무슨 값인지 알려면, AND 연산을 활용한다.
10101 & 1 <<i
3번째 비트 값: 10101 & (1<<3) = 10101 & 01000 ->0
4번째 비트 값: 10101 & (1<<4) = 10101 & 10000 -> 10000이처럼 결과값이 0인 경우에는 i번째 비트 값이 0인 것을 알 수 있다.(반대로 0이 아니면 무조건 1)
문제 추천
- 백준 S4_2503 숫자 야구
- 백준 S3_2606 바이러스
- 백준 S1_2178 미로 탐색
- 백준 S1_1697 숨바꼭질
- 백준 G5_14500 테트로미노