[백준] 1520번 내리막길 - 파이썬/DFS

https://www.acmicpc.net/problem/1520

import sys
sys.setrecursionlimit(100000)
M,N = map(int,sys.stdin.readline().split())
N,M = M,N # 편하게 보기 위해 M,N 스왑
graph = []

for i in range(N):
    temt = list(map(int,sys.stdin.readline().split()))
    graph.append(temt)

DP = [ [-1] *M for _ in range(N)]

def dfs(x,y):

    if (x,y) == (N-1,M-1):
        return 1

    if DP[x][y]==-1:
        DP[x][y]=0

        dx = [1,0,-1,0]
        dy = [0,1,0,-1]

        for i in range(4):

            nx = x + dx[i]
            ny = y + dy[i]

            if 0<=nx<N and 0<=ny<M and graph[nx][ny]<graph[x][y]:
                DP[x][y] += dfs(nx,ny)

    return DP[x][y]

print(dfs(0,0))

처음에는 그냥 DFS로 풀었는데 시간 초과가 발생했다.

그래서 DP를 적용시켜야된다는 것을 직감했다.

DP그래프의 좌표는 해당 좌표에서 종점까지 가는 방법의 갯수이다.

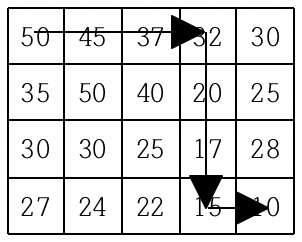
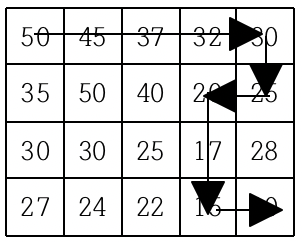
여기서 (0,3) 32값을 가진 칸을 보자.

해당 칸은 (0,4), (1,3) 으로 퍼져나갈 수 있다.

또한, (0,4), (1,3) 에서 종점까지 가는 방법의 수는 dfs(0,4), dfs(1,3) 로 구할 수 있다.

즉, (0,3)에서 종점까지 가는 방법의 수는 dfs(0,4) + dfs(1,3) 과 같다.

원래는 dfs(0,3)을 해야했지만 기존에 구했던 dfs값을 재활용하여 시간복잡도를 줄일 수 있다.

이런 식으로 가장 끝의 점부터 (0,0)까지 타고 올라오면 정답을 구할 수 있다.